
振幅変調がある時間波形の変調成分を抽出するには、波形の包絡線を求める必要があります。包絡線はヒルベルト変換という数学的処理で簡単に求めることが出来ますが、ここではPythonでヒルベルト変換を使い包絡線を求める簡単なコードを紹介します。
こんにちは。wat(@watlablog)です。
今回は有名な信号処理の1つ、ヒルベルト変換を使った時間波形の包絡線を求める方法を紹介します!
ヒルベルト変換や解析信号に関してはわかりやすく説明されている手持ちの書籍等が見当たらなかったので、今回は小野測器さんのコラムや京都大学さんの講義資料(直リンクは避けます)、Wikiを始めとしたインターネットの情報で学習をしました。
本記事の序盤はメモ程度の内容なので、「はやくコードが見たい!」という方は目次ジャンプをしてみて下さい!
ヒルベルト変換は波形の瞬時振幅と瞬時位相を計算する
ヒルベルト変換は何に役立つ?
ヒルベルト変換(Hilbert Transform)は、技術者の間では「波形の包絡線を求める時に使うもの」という認識の方が多いと思われますが、その本質は実数領域の時系列信号に対して、その直交信号を作り出すという所にあると考えられます。
僕もこの記事を書く前は単に包絡線を計算するためだけの技術かと思っていました!
この直交信号を作り出すことで、波形の情報をリアルタイムに得ることができるようになるわけですが、結局の所は包絡線を求めることに最も使われているようです。
ここでいう包絡線(エンベロープ:Envelope)とは、以下の図に示すように振動している波形の振幅成分を時系列でトレースしたようなものです。
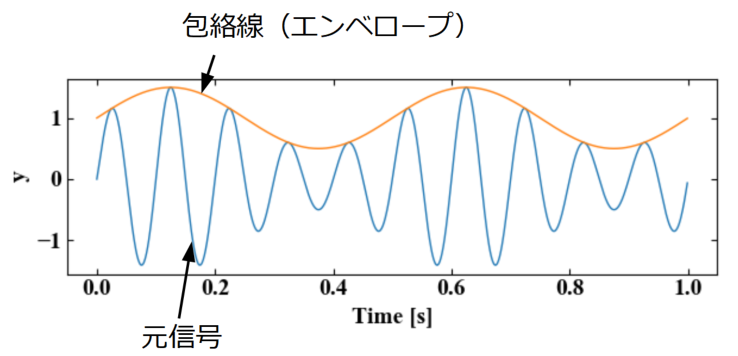
この図は元信号が一定の周波数(ベースバンド周波数)で振動しているのに対して、振幅だけがある周波数でさらに変動している波形です。
このような波形を振幅変調(AM:Amplitude Modulation)波形と呼びます。
AMラジオのAMという文字はまさしくこの振幅変調を意味しており、音声信号をベースバンド信号の振幅成分に乗せて受信者へ音を運ぶ技術を使っています。
以下の図は参考ですが、音声信号が我々のもとに届くまでの流れを示した図です。
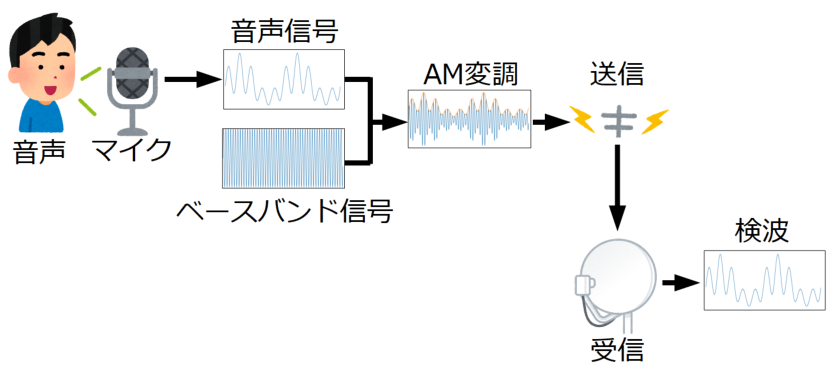
受信した先で「検波」の工程がありますが、この部分で包絡線成分を検出するという技術が使われています。
直接音声を電波で飛ばさないのは、低周波過ぎて飛ばせないからかな?
人間の可聴域は20[Hz]~20[kHz], AMラジオの周波数帯は大体数百[kHz]~数[MHz]だから特に近い周波数ってわけでもなく、送信に問題無く設定されていそうだね。
時間波形を複素数で考えて瞬間の波形情報を得る
ではどうやって包絡線を検出したら良いかを考えます。
下の図は振幅\(A\)が一定の正弦波を例にとっていますが、振幅が変調していないので、正しい包絡線は各正弦波のピークを横に繋いだ一直線になるはずです。
しかし、正弦波は中立点を境に振動しているので、包絡線を描くためには縦軸の変化が、振幅が小さくなっているから変化しているのかそうでないのかの見極めが必要です。
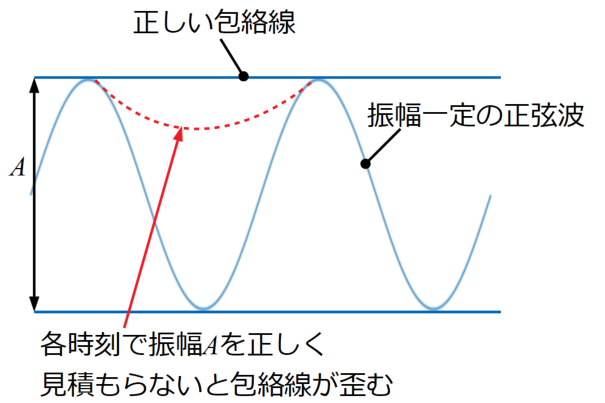
つまり各時刻で波形の振幅成分を正しく見積もる必要があり、特に瞬間瞬間の振幅のことを瞬時振幅(Instantaneous Amplitude)と呼び、この瞬時振幅が正に包絡線を意味します。
このページでは専門的な理屈や式の詳細展開はしませんが、この瞬時振幅を得るために、ヒルベルト変換では実際の信号を複素平面として捉え、実信号に直交する信号を作り出す方法を使っています。
以下の図は単一周波数の波形の例ですが、実信号(cos波で示す)を実部\(Re\)の振幅\(A\)の波とした時に、虚部\(Im\)として直交した信号(sin波で示す)を得ることができます。
実信号を実部と虚部で表現するアプローチをとり、瞬時振幅\(A(t)\)と瞬時位相(Instantaneous Phase)\(\theta(t)\)を求めていくというのがヒルベルト変換で実施している計算の概要です。
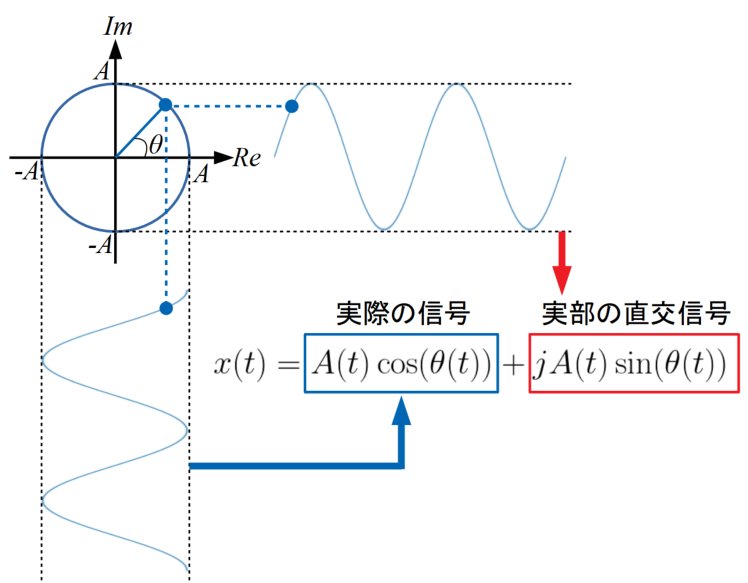
ここから先の式は畳み込み(コンボリューション)とか符号関数、フーリエ変換の理論を使うので、僕はうまく説明できる自信が無いので、Wikiとかに丸投げします!
波形の瞬間の振幅成分がわかれば包絡線が描ける!ということが重要です!
瞬時振幅の式
瞬時振幅\(A(t)\)は上で解説した複素信号\(x(t)\)の実部を\(Re\)、虚部を\(Im\)とすれば次の式で求めることが可能です。
これは通常のフーリエ変換と同様ですね。
瞬時位相の式
瞬時位相\(\theta(t)\)は次の式で求めることが可能です。これも通常のフーリエ変換と同様ですね。
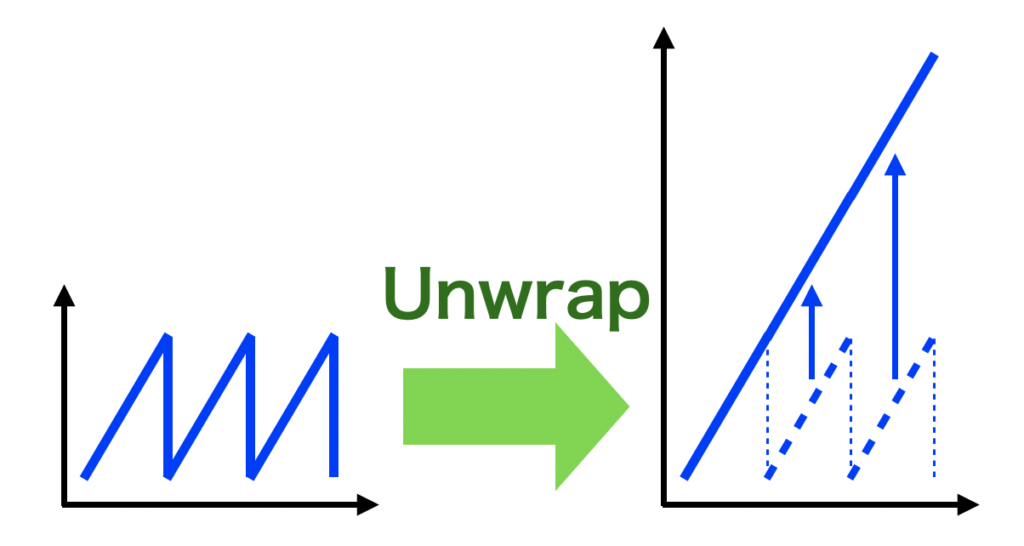
ただし位相角はアークタンジェントで求めるため、アンラップ処理が必要です。
アークタンジェントで求めた位相角は\(-\pi \leq \theta \leq \pi \)の範囲をとるため、下図左のようにのこぎり波形状になります。それを右の図のように連続的に接続する計算をアンラップと呼びます。
瞬時周波数の式
瞬時位相が求まれば瞬時周波数(Instantaneous Frequency)も求めることができます。
周波数は位相角を微分し、角周波数を周波数に変換することで計算します。また実際の計測データは離散データであるため、微分の刻み幅を考慮する必要があり次式で求めます。
ここで\(f_{s}\)はサンプリングレート(\(=\frac{1}{dt}\))です。
自分でヒルベルト変換の手順を追ってみた
ヒルベルト変換を使った包絡線検出は、SciPyの関数を使えばあっけなく求まりますが、この章ではあえて手順を踏んで計算の理解を深めようと思います。記事の最後に関数を使った方法を示しますので、はやく知りたい方は下にスクロールをお願いします!
色々理屈はありますが、実は離散系のヒルベルト変換を利用した包絡線検出はごく簡単な手順で実装することが可能です。
以下のフローは実関数(測定データ等の時間波形)から包絡線を求めるための手順です。
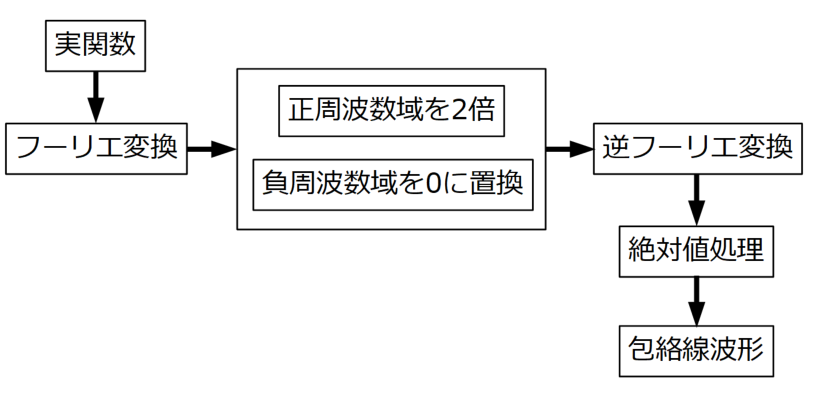
今回フーリエ変換はFFT、逆フーリエ変換はIFFTと高速フーリエ変換を使いますが、それぞれの方法は既に当WATLABブログで紹介しました。
ご興味のある方は是非「PythonでFFTとIFFT!逆フーリエ変換で時間波形を作る」という記事を見てみて下さい!
それでは以下から実際にコードを使いながら説明していきます!
全コード
詳細説明より先にまずは全コードを示します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 |
import numpy as np from scipy import fftpack from matplotlib import pyplot as plt # FFTをする関数 def fft_ave(data, samplerate, Fs): fft = fftpack.fft(data) # FFT(実部と虚部) fft_amp = np.abs(fft / (Fs / 2)) # 振幅成分を計算 fft_axis = np.linspace(0, samplerate, Fs) # 周波数軸を作成 return fft, fft_amp, fft_axis # サンプルの時間領域信号を生成 dt = 0.001 t = np.arange(0, 1, dt) wave = np.cos(2 * np.pi * 50 * t) wave *= (1 + 0.5 * np.sin(2 * np.pi * 2 * t)) wave *= (1 + 0.5 * np.sin(2 * np.pi * 10 * t)) # FFTする fft, fft_amp, fft_axis = fft_ave(wave, 1 / dt, len(wave)) # 負周波数域(ナイキスト周波数以降)を0にする(実部と虚部の両方) zeros = np.zeros(int(len(fft) / 2)) fft[int(len(fft) / 2):len(fft)] = zeros # 正周波数域(ナイキスト周波数まで)を2倍する fft *= 2 # 操作した実部と虚部を持つ周波数波形をIFFTし、絶対値をとる(包絡線を得る) ifft_time = np.abs(fftpack.ifft(fft)) # ここからグラフ描画 # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure() ax1 = fig.add_subplot(211) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') ax2 = fig.add_subplot(212) ax2.yaxis.set_ticks_position('both') ax2.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('Frequency [Hz]') ax1.set_ylabel('x(f)') ax2.set_xlabel('Time [s]') ax2.set_ylabel('x(t)') # データの範囲と刻み目盛を明示する。 ax1.set_xticks(np.arange(0, 1 / dt, 20)) ax1.set_xlim(0, 100) # データプロットの準備とともに、ラベルと線の太さ、凡例の設置を行う。 ax1.plot(fft_axis, fft_amp, label='signal', lw=1) ax2.plot(t, wave, label='original', lw=1) ax2.plot(t, ifft_time, label='envelope', lw=1) fig.tight_layout() plt.legend() # グラフを表示する。 plt.show() plt.close() |
相変わらずグラフ表示設定が長いですが、それでは詳細を説明していきます。
①実関数を用意する
まずは包絡線算出に使用する波形を生成します。ここでは基本の波に2種類の振幅変調を重畳させた波として表現しています。
|
1 2 3 4 5 6 |
# サンプルの時間領域信号を生成 dt = 0.001 t = np.arange(0, 1, dt) wave = np.cos(2 * np.pi * 50 * t) wave *= (1 + 0.5 * np.sin(2 * np.pi * 2 * t)) wave *= (1 + 0.5 * np.sin(2 * np.pi * 10 * t)) |
グラフに表示させると以下の図になります。
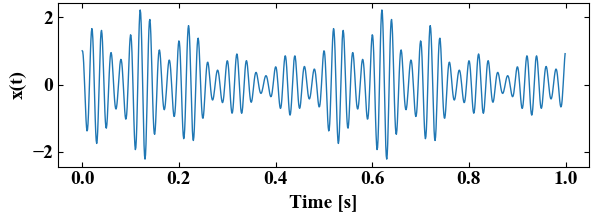
②フーリエ変換する
次は高速フーリエ変換のコードです。ここではFFT部分を関数として定義しています。この関数は波形dataと波形のサンプリングレートsamplerate(何Hzでサンプリングしているデータか、時間刻みdtの逆数)、フレームサイズFs(データ長)を引数としています。
|
1 2 3 4 5 6 7 8 9 |
# FFTをする関数 def fft_ave(data, samplerate, Fs): fft = fftpack.fft(data) # FFT(実部と虚部) fft_amp = np.abs(fft / (Fs / 2)) # 振幅成分を計算 fft_axis = np.linspace(0, samplerate, Fs) # 周波数軸を作成 return fft, fft_amp, fft_axis # FFTする fft, fft_amp, fft_axis = fft_ave(wave, 1 / dt, len(wave)) |
本来であれば実部と虚部を持ったfftだけを戻り値にすれば十分なのですが、便宜上振幅成分fft_ampと周波数軸fft_axisも設定しました(メイン文で色々やるのが好きではないので…)。
③正負の周波数域の処理をする
次にFFTした実部と虚部を持つ複素数波形fftの操作を行います。
|
1 2 3 4 5 6 |
# 負周波数域(ナイキスト周波数以降)を0にする(実部と虚部の両方) zeros = np.zeros(int(len(fft) / 2)) fft[int(len(fft) / 2):len(fft)] = zeros # 正周波数域(ナイキスト周波数まで)を2倍する fft *= 2 |
正と負の周波数域というのがわかりにくいと思いますが、FFTの場合負の周波数領域の値はナイキスト周波数以上に現れます。 ナイキスト周波数までを正の周波数、ナイキスト周波数以上を負の周波数と捉えています。
ヒルベルト変換のためには、負の周波数域をゼロにして正の周波数域を2倍する必要がありますので、まずゼロ置換をして複素数全体を2倍する手順をとりました。
④逆フーリエ変換と絶対値処理で包絡線算出
最後に逆フーリエ変換と絶対値処理を一度に実施し、包絡線を得ます。
|
1 2 |
# 操作した実部と虚部を持つ周波数波形をIFFTし、絶対値をとる(包絡線を得る) ifft_time = np.abs(fftpack.ifft(fft)) |
実行結果
以下の図が実行結果です。上がFFTの振幅成分、下が時間波形で、実関数とエンベロープ波形を重ねています。
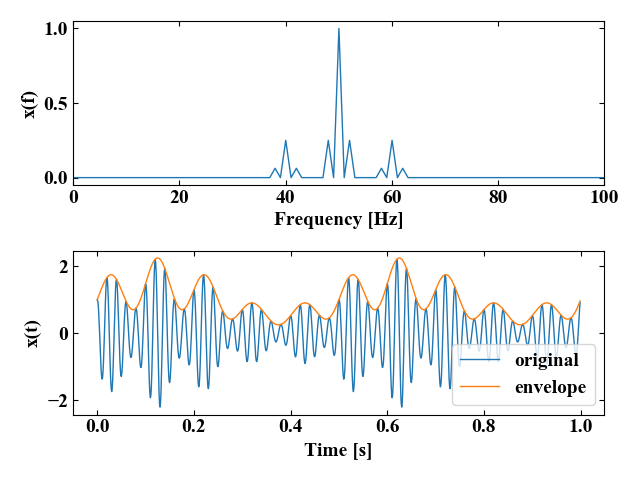
包絡線は見事実関数にフィットしました!
SciPyのhilbert関数を使う場合のヒルベルト変換コード
全コード
それでは本命です。SciPyのhilbert関数を使った包絡線検出プログラムの全コードを以下に示します。
これはもう説明不要でしょう。包絡線は「np.abs(signal.hilbert(wave))」のたった1行で求まってしまいます!
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 |
import numpy as np from scipy import signal import matplotlib.pyplot as plt # サンプルの時間領域信号を生成 dt = 0.001 t = np.arange(0, 1, dt) wave = np.cos(2 * np.pi * 50 * t) wave *= (1 + 0.5 * np.sin(2 * np.pi * 2 * t)) wave *= (1 + 0.5 * np.sin(2 * np.pi * 10 * t)) # ヒルベルト変換と絶対値処理を実行し包絡線を得る amplitude_envelope = np.abs(signal.hilbert(wave)) # ここからグラフ描画 # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure() ax1 = fig.add_subplot(111) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('Time [s]') ax1.set_ylabel('y') # データプロットの準備とともに、ラベルと線の太さ、凡例の設置を行う。 ax1.plot(t, wave, label='original', lw=1) ax1.plot(t, amplitude_envelope, label='envelope', lw=1) plt.legend() # レイアウト設定 fig.tight_layout() # グラフを表示する。 plt.show() plt.close() |
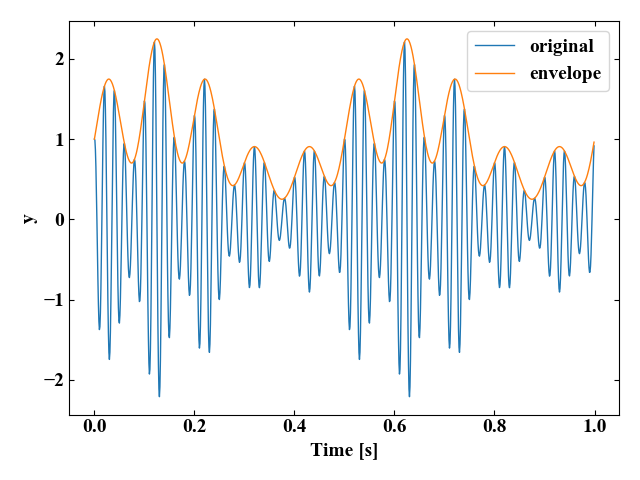
実行結果
実行結果も先ほど自作したコードと同じです。1行で終わるならこっちの方がよっぽど良いですね!
追記:瞬時周波数を求めるPythonコード
せっかくヒルベルト変換後の解析波形として複素信号を求めているため、瞬時振幅/瞬時位相/瞬時周波数を同時に求めてプロットしてみましょう!
周波数の変化を計測するため、サンプル波形はチャープ信号(時間で周波数が変化する信号)を用います。
以下が全コードですが、今回はこの記事を初めて書いた日から2年以上経過していることから上のコードと書き方を変えてみました。
def hilbert()の中で瞬時振幅、瞬時位相、瞬時周波数を求めていますが、フーリエ変換もこの中で行いヒルベルト変換としての機能をまとめました。
また、mataplotlibによるプロットも関数化したり、メイン実行文を「if __name__ == '__main__':」の中に記入したり、関数の一段下に簡易的なdocstringを書いたりしています。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 |
import numpy as np from scipy import signal from scipy import fftpack import matplotlib.pyplot as plt def create_chirp(t_end, dt, start, end): '''チャープ信号を生成''' t = np.arange(0, t_end, dt) y = signal.chirp(t, f0=start, f1=end, t1=t_end, method='linear') return t, y def plot(t, y, instantaneous_amp, instantaneous_frequency, instantaneous_phase): '''matplotlibで可視化''' # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure() ax1 = fig.add_subplot(311) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') ax2 = fig.add_subplot(312) ax2.yaxis.set_ticks_position('both') ax2.xaxis.set_ticks_position('both') ax3 = fig.add_subplot(313) ax3.yaxis.set_ticks_position('both') ax3.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('Time [s]') ax1.set_ylabel('Amplitude') ax2.set_xlabel('Time [s]') ax2.set_ylabel('Frequency [Hz]') ax3.set_xlabel('Time [s]') ax3.set_ylabel('Phase [rad]') # スケール設定 #ax2.set_ylim(0, 120) # データプロット ax1.plot(t, y, label='original', lw=1, color='red') ax1.plot(t, instantaneous_amp, label='instant amplitude', lw=1, color='blue') ax2.plot(t, instantaneous_frequency, label='instant frequency', lw=1, color='blue') ax3.plot(t, instantaneous_phase, label='instant phase', lw=1, color='blue') # レイアウト設定 fig.tight_layout() # グラフを表示する。 plt.show() plt.close() def hilbert(yt, dt): '''ヒルベルト変換''' # フーリエ変換 spectrum = fftpack.fft(yt) # 負周波数域(ナイキスト周波数以降)を0にする(実部と虚部の両方) zeros = np.zeros(int(len(spectrum) / 2)) spectrum[int(len(spectrum) / 2):len(spectrum)] = zeros # 正周波数域(ナイキスト周波数まで)を2倍する spectrum *= 2 #実部と虚部から瞬時振幅と瞬時位相を計算する zt = fftpack.ifft(spectrum) re = zt.real im = zt.imag # 瞬時振幅 instantaneous_amp = np.sqrt(re ** 2 + im ** 2) # 瞬時位相とアンラップ処理 instantaneous_phase = np.arctan2(im, re) instantaneous_phase = np.unwrap(instantaneous_phase) # 瞬時周波数(位相角の微分と時間刻み影響を考慮) instantaneous_frequency = ((1 / dt) / (2 * np.pi)) * np.gradient(instantaneous_phase) return instantaneous_amp, instantaneous_frequency, instantaneous_phase if __name__ == '__main__': # チャープ信号の開始周波数と終了周波数 f_start = 1 f_end = 10 # 時間刻み dt = 0.0001 # チャープ信号を取得 t, y = create_chirp(10, dt, f_start, f_end) # ヒルベルト変換を実行 instantaneous_amp, instantaneous_frequency, instantaneous_phase = hilbert(y, dt) # プロットを表示 plot(t, y, instantaneous_amp, instantaneous_frequency, instantaneous_phase) |
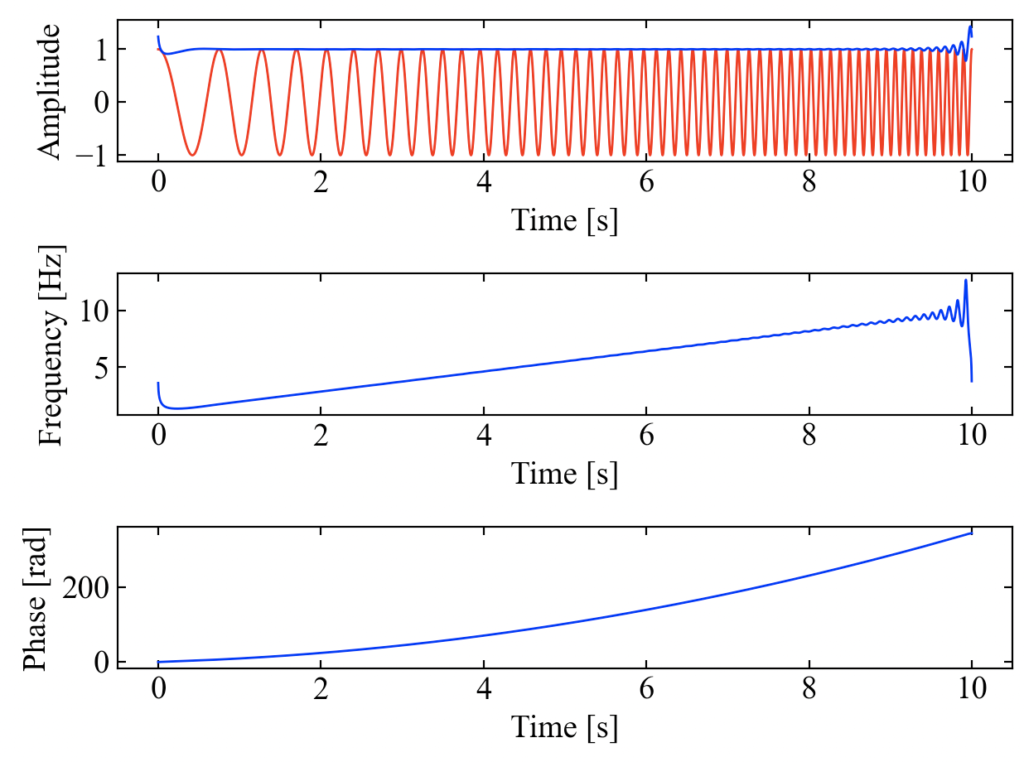
以下が実行結果です。1[Hz]から10[Hz]まで変化するチャープ信号の瞬時周波数が計測されました。
中間部はリニアに変化している様子が確認できますが、信号の端部でゆれているのは端部が切れているためにうまく計算されていないのかも知れません。今回フーリエ変換時に窓関数等は使っていないこと等も影響しているのかも。
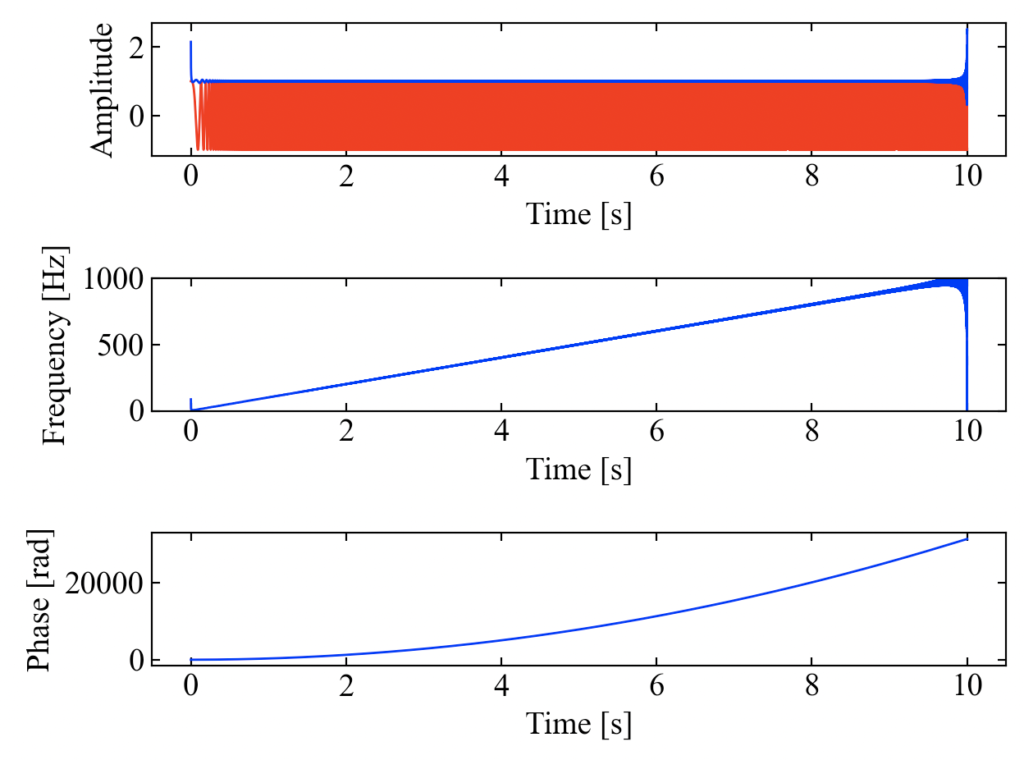
次は1[Hz]から1000[Hz]まで一気に周波数を上げてみた結果を以下に示します。先ほどと同様に想定通りの結果が得られたようです。
まとめ
本記事ではヒルベルト変換が何に使われているか、どういう計算をしているかを紹介しました。
また、アルゴリズムの確認のためにあえて自作したヒルベルト変換コードで包絡線を計算し、SciPyのhilbert関数で実行した時と同じように包絡線が求まることを確認しました。
最後に追記として、瞬時周波数まで求める式やコードも紹介しました。これでヒルベルト変換が使えるようになったと言えそうですね。
有名なヒルベルト変換ですが、まずは使えるレベルになりました!
Twitterでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています!

 ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!
ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!
Wat様
勉強になりました。下側(yがマイナス側)のEnvelopeを出すにはどこを変えればよいのでしょうか?
ご訪問ありがとうございます。
本記事の波形に関しては、得られたEnvelopeに対して-1を乗ずれば解決すると思いますがどうでしょうか?
しかし、もし上側と下側で振幅成分が異なる場合は今回のヒルベルト変換では対応できないかも知れません。
(実際の波形は複雑な場合が多いですので)