様々な種類の信号を生成できるようにしておくのは、シミュレーション、または実験を行う上で有用です。正弦波はよく利用されていますが、ここではPythonを使って周波数が時々刻々と変わる周波数スイープ正弦波を作る方法を解説します。
こんにちは。wat(@watlablog)です。
様々な科学技術の分野で、信号処理は効果的な解決策を与えます。ここでは波形生成として、チャープ信号をPythonで作る方法を紹介します!
チャープ信号とは?
チャープ信号とは、聞きなれない方も多いと思いますが、要は周波数が時間で変化する正弦波のことです。
このページで最終的に作る信号は以下の図のような正弦波です。
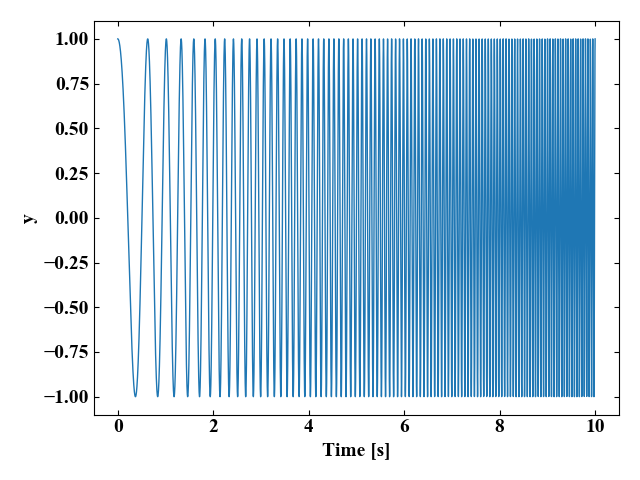
これがチャープ信号です。正弦波の周波数が低周波から高周波まで変化しているのがわかると思います。
シミュレーションでも実験でも、モデルの特性を同定するために、加振信号を与えて応答を見ることは、技術者であればよくやることだと思います。
では、この周波数スイープ正弦波の作り方を説明していきます。
Pythonでチャープ信号を作る
まずは基本のコードを書いてみる
以下がチャープ信号の生成プログラムです。正直y=の部分しか無いのでめちゃくちゃ簡単ですが、chirp関数は時間軸配列tを使って、f0で指定した開始周波数からf1の周波数まで周波数を変化させる関数です。f1の周波数に達する時間はt1で指定します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 |
from scipy.signal import chirp import numpy as np import matplotlib.pyplot as plt t = np.linspace(0, 10, 10000) y = chirp(t, f0=1, f1=20, t1=10, method='linear') # ここからグラフ描画 # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure() ax1 = fig.add_subplot(111) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('Time [s]') ax1.set_ylabel('y') # データプロットの準備とともに、ラベルと線の太さ、凡例の設置を行う。 ax1.plot(t, y, label='chirp', lw=1) # レイアウト設定 fig.tight_layout() # グラフを表示する。 plt.show() plt.close() |
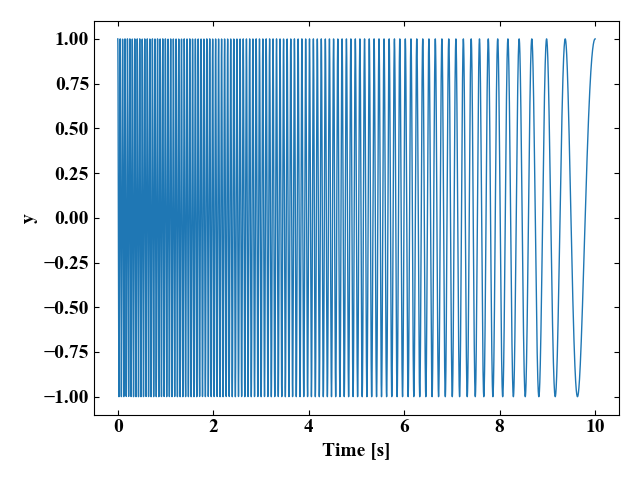
上のチャープ信号は1Hzから20Hzの周波数スイープをしていますが、f0を20Hz、f1を1Hzとすることで逆方向のスイープをさせることも可能です。
FFTして周波数波形を見てみる
「PythonでFFT!SciPyのFFTまとめ」でデータを自由にFFTすることができるようになったので、チャープ信号の周波数波形を見てみましょう。
以下の図は100Hzから5000Hzまで周波数スイープした波形です。周波数的に非常にフラットな特性を持っていることがわかりました。
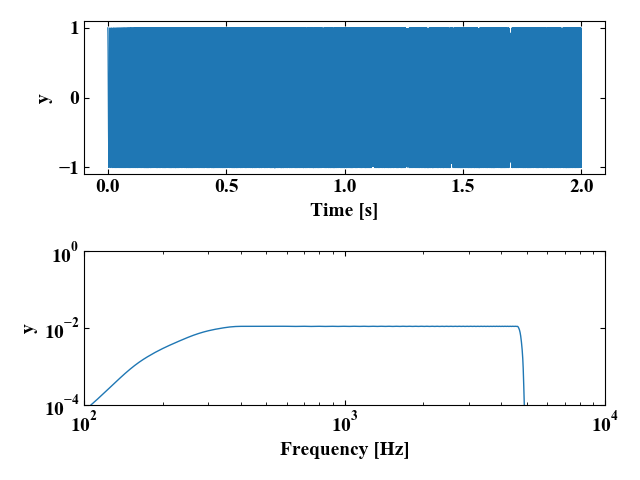
以下は周波数波形まで含めて計算するコードです。実行することで上のグラフが表示されます。先ほどはchripを直接importしていましたが、FFTでも窓関数でsignalを使っているので、importはsignalのみとし、チャープ信号はsignal.chripで作成しています。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 |
from scipy import signal from scipy import fftpack import numpy as np import matplotlib.pyplot as plt # オーバーラップ処理 def ov(data, samplerate, Fs, overlap): Ts = len(data) / samplerate # 全データ長 Fc = Fs / samplerate # フレーム周期 x_ol = Fs * (1 - (overlap / 100)) # オーバーラップ時のフレームずらし幅 N_ave = int((Ts - (Fc * (overlap / 100))) / (Fc * (1 - (overlap / 100)))) # 抽出するフレーム数(平均化に使うデータ個数) array = [] # 抽出したデータを入れる空配列の定義 # forループでデータを抽出 for i in range(N_ave): ps = int(x_ol * i) # 切り出し位置をループ毎に更新 array.append(data[ps:ps + Fs:1]) # 切り出し位置psからフレームサイズ分抽出して配列に追加 return array, N_ave # オーバーラップ抽出されたデータ配列とデータ個数を戻り値にする # 窓関数処理(ハニング窓) def hanning(data_array, Fs, N_ave): han = signal.hann(Fs) # ハニング窓作成 acf = 1 / (sum(han) / Fs) # 振幅補正係数(Amplitude Correction Factor) # オーバーラップされた複数時間波形全てに窓関数をかける for i in range(N_ave): data_array[i] = data_array[i] * han # 窓関数をかける return data_array, acf # FFT処理 def fft_ave(data_array, samplerate, Fs, N_ave, acf): fft_array = [] for i in range(N_ave): fft_array.append(acf * np.abs(fftpack.fft(data_array[i]) / (Fs / 2))) # FFTをして配列に追加、窓関数補正値をかけ、(Fs/2)の正規化を実施。 fft_axis = np.linspace(0, samplerate, Fs) # 周波数軸を作成 fft_array = np.array(fft_array) # 型をndarrayに変換 fft_mean = np.mean(fft_array, axis=0) # 全てのFFT波形の平均を計算 return fft_array, fft_mean, fft_axis # 波形生成 samplerate = 25600 x = np.arange(0, 51200)/samplerate data = signal.chirp(x, f0=100, f1=5000, t1=2, method='linear') Fs = 4096 # フレームサイズ overlap = 75 # オーバーラップ率 # 作成した関数を実行:オーバーラップ抽出された時間波形配列 time_array, N_ave = ov(data, samplerate, Fs, overlap) # 作成した関数を実行:ハニング窓関数をかける time_array, acf = hanning(time_array, Fs, N_ave) # 作成した関数を実行:FFTをかける fft_array, fft_mean, fft_axis = fft_ave(time_array, samplerate, Fs, N_ave, acf) # ここからグラフ描画 # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure() ax1 = fig.add_subplot(211) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') ax2 = fig.add_subplot(212) ax2.yaxis.set_ticks_position('both') ax2.xaxis.set_ticks_position('both') ax2.set_xticks(np.arange(0, samplerate, 1000)) ax2.set_xlim(100, 10000) ax2.set_xscale('log') ax2.set_ylim(0.0001, 1) ax2.set_yscale('log') # 軸のラベルを設定する。 ax1.set_xlabel('Time [s]') ax1.set_ylabel('y') ax2.set_xlabel('Frequency [Hz]') ax2.set_ylabel('y') # データプロットの準備とともに、ラベルと線の太さ、凡例の設置を行う。 ax1.plot(x, data, label='sawtooth', lw=1) ax2.plot(fft_axis, fft_mean, label='sawtooth', lw=1) # レイアウト設定 fig.tight_layout() # グラフを表示する。 plt.show() plt.close() |
FFTの詳細は「PythonでFFT!SciPyのFFTまとめ」を参照下さい。
まとめ
周波数をスイープアップ、もしくはスイープダウンさせるチャープ信号生成の方法をPythonで示しました。
Pythonのscipyを使えば簡単に信号を生成できることを確認することができました。
生成したチャープ信号の周波数特性はフラットであることを確認しました。
チャープ信号は関数で一発生成できましたね!
Twitterでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています!

 ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!
ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!
コメント