Pythonの過渡応答解析で力を滑らかにかけて応答の違いを見る

振動の時刻歴応答シミュレーションを行う場合、加振の信号は多大に影響します。今回は滑らかに振幅増加する信号を使った場合とそうでない場合で、応答波形がどう変化するのかをPythonで確認していきます。

こんにちは。wat(@watlblog)です。
今回はこれまで実施してきたシミュレーションを少し深堀していきます。運動方程式への入力波形に差異を与えて応答を確認していきます！

目次（項目クリックでジャンプできます）

時刻歴応答解析に使う信号について

なぜ滑らかに振幅増加する波形を使うか？

この記事を書くことになったきっかけは、以下のツイートに頂いたリプです。

過渡応答の結果が安定していないのは、振幅を一定にしているためと思われます。初めから大きな振幅を入れてしまうとパルス入力となり定常応答と一致しなくなります。比較する際には振幅をはじめは0.0とし、時間とともに少しずつ大きくしていくのが一般的です。ご参考までに。
— ゆうげん☺@10/27にGetFEM++Hack-a-thon (@tkoyama010) July 3, 2019

「Pythonで1自由度振動系の過渡応答の周波数分析をやってみた」では1自由度振動系に正弦波を与えていました。そしてその応答の時間波形は初期からしばらく安定しないような挙動をしていました。

そんな中頂いたこのリプ。プロフから察するにその道の専門家。

「詳しい人からのアドバイスは即聞いて試してみよう」がモットーなので、上記リプの理由から滑らかに振幅増加する信号でシミュレーション結果がどう変化するかを見てみたいと思います。

今回加振に使う滑らかな信号

今回は、「Pythonで滑らかに振幅増加する正弦波を作る1つの簡単な例」で作ったスムース関数を加振の信号に使います。

加振力にかける係数波形は以下の図の係数考慮シグモイド関数とtanh(ハイパボリックタンジェント)を組み合わせたもの。

ここでは便宜上smooth関数と呼びます（カッコいいので）。

式は以下です。

$$y=\frac{\tanh x}{1+ae^{-x}}$$

例えば10[Hz]の正弦波だと、以下の図のように滑らかになります。

今回応答を確認する運動方程式

モデル図と運動方程式は当ブログではお馴染み、1自由度の振動系です。

$$m\ddot{x}+c\dot{x}+kx=F$$
$$F=A\sin (2\pi ft)$$

Pythonでシミュレーション！入力波形の違いを見る！

全コード

今回実行するコードはこちら。加振の周波数は視認しやすいように1[Hz]にしています。def smoothが上に示したスムース関数で、def funcの中でスムース関数を使っている方をアクティブにしています。その上に書いてある#dx2dtのシャープを外して、下のdx2dtにシャープを付けることでスムース関数を考慮しない応答を得ることが出来ます。

import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt

def smooth(x):
    a = 30
    y = np.tanh(x) / (1 + a * np.exp(- x))
    return y

# mkc force system
def func(state, t, m, k, c, A, f):
    x1, x2 = state
    #dx2dt = - (c / m) * x2 - (k / m) * x1 + A * np.cos(2 * np.pi * f * t) #スムース関数無し
    dx2dt = - (c / m) * x2 - (k / m) * x1 + A * smooth(t) * np.cos(2 * np.pi * f * t) #スムース関数有り
    return [x2, dx2dt]


m = 0.5                         # 質量[kg]
k = 1000                        # 剛性[N/m]
c = 0.1                         # 減衰係数[N・s/m]
A = 1                           # 強制外力の振幅[N]
state0 = [0.0, 0.0]             # 初期値[x0, v0]
f = 1                           # 加振周波数[Hz]

t0 = 0                          # 初期時間[s]
tf = 50                         # 終了時間[s]
dt = 0.005                      # 時間刻み[s]

t = np.arange(t0, tf + dt, dt)  # 時間軸配列

# ここからグラフ描画
# フォントの種類とサイズを設定する。
plt.rcParams['font.size'] = 14
plt.rcParams['font.family'] = 'Times New Roman'

# 目盛を内側にする。
plt.rcParams['xtick.direction'] = 'in'
plt.rcParams['ytick.direction'] = 'in'

# グラフの上下左右に目盛線を付ける。
fig = plt.figure()
ax1 = fig.add_subplot(111)
ax1.yaxis.set_ticks_position('both')
ax1.xaxis.set_ticks_position('both')

# 軸のラベルを設定する。
ax1.set_xlabel('Time [s]')
ax1.set_ylabel('Displacement [m]')

# データの範囲と刻み目盛を明示する。
#ax1.set_xticks(np.arange(0, 10000, 100))
#ax1.set_xlim(10, 100)

sol = odeint(func, state0, t, args=(m, k, c, A, f))
ax1.plot(t, sol[:, 0])

# レイアウト
fig.tight_layout()

# グラフを表示する。
plt.show()
plt.close()

import numpy as np

from scipy.integrate import odeint

import matplotlib.pyplot as plt

def smooth(x):

a = 30

y = np.tanh(x) / (1 + a * np.exp(- x))

return y

# mkc force system

def func(state, t, m, k, c, A, f):

x1, x2 = state

#dx2dt = - (c / m) * x2 - (k / m) * x1 + A * np.cos(2 * np.pi * f * t) #スムース関数無し

dx2dt = - (c / m) * x2 - (k / m) * x1 + A * smooth(t) * np.cos(2 * np.pi * f * t) #スムース関数有り

return [x2, dx2dt]

m = 0.5 # 質量[kg]

k = 1000 # 剛性[N/m]

c = 0.1 # 減衰係数[N・s/m]

A = 1 # 強制外力の振幅[N]

state0 = [0.0, 0.0] # 初期値[x0, v0]

f = 1 # 加振周波数[Hz]

t0 = 0 # 初期時間[s]

tf = 50 # 終了時間[s]

dt = 0.005 # 時間刻み[s]

t = np.arange(t0, tf + dt, dt) # 時間軸配列

# ここからグラフ描画

# フォントの種類とサイズを設定する。

plt.rcParams['font.size'] = 14

plt.rcParams['font.family'] = 'Times New Roman'

# 目盛を内側にする。

plt.rcParams['xtick.direction'] = 'in'

plt.rcParams['ytick.direction'] = 'in'

# グラフの上下左右に目盛線を付ける。

fig = plt.figure()

ax1 = fig.add_subplot(111)

ax1.yaxis.set_ticks_position('both')

ax1.xaxis.set_ticks_position('both')

# 軸のラベルを設定する。

ax1.set_xlabel('Time [s]')

ax1.set_ylabel('Displacement [m]')

# データの範囲と刻み目盛を明示する。

#ax1.set_xticks(np.arange(0, 10000, 100))

#ax1.set_xlim(10, 100)

sol = odeint(func, state0, t, args=(m, k, c, A, f))

ax1.plot(t, sol[:, 0])

# レイアウト

fig.tight_layout()

# グラフを表示する。

plt.show()

plt.close()

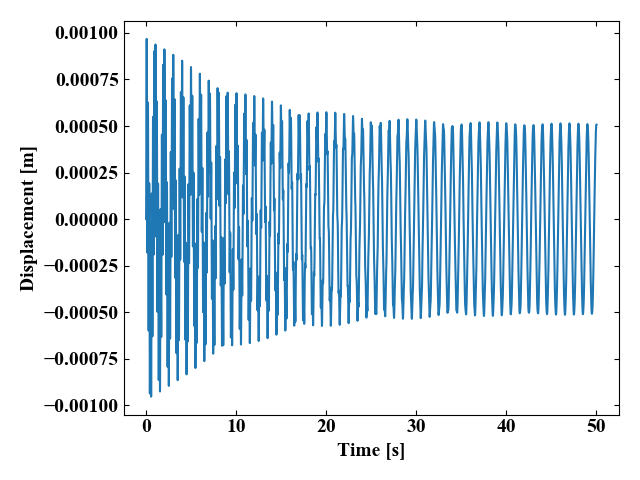
スムース関数が無い場合

まずはスムース関数を適用しない場合の応答です。

30[s]ほど経ってようやく定常振動になって来た状態と思いますが、初期はかなり暴れている様子です。

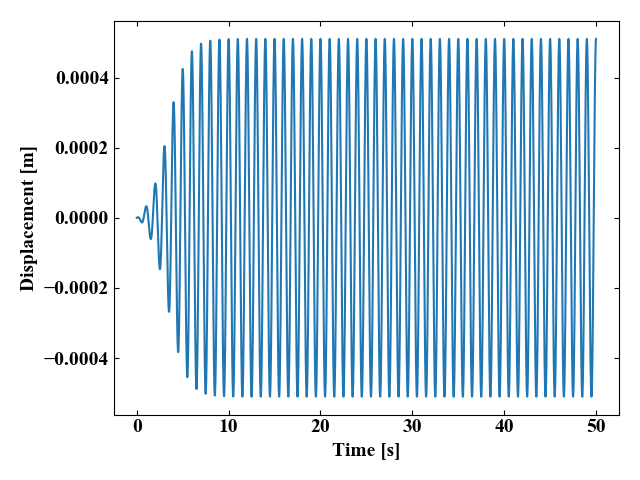
スムース関数を適用した場合

続いてスムース関数を適用させた場合の結果を以下に示します。この結果は10[s]くらいには振動が安定していますね。

同じモデルを使っていても、入力波形によって結果がこんなに変わるということがわかりました！

まとめ

強制振動の時刻歴応答シミュレーションでは急激に振動させるとパルス入力となってしまい、応答結果が初期で安定しませんでした。

加振信号に対してシグモイド関数とtanh関数を組み合わせて作ったスムース処理を行った場合は安定するまでの時間がはやくなるといった効果がありました。

もちろん系のパラメータや共振付近によって、今回の方法は万能な処理とは言えないと思いますが、入力波形が結果に大きく影響していますよという実証にはなったかと思います。

シミュレーションの入力波形の重要さがわかりましたね！

Twitterでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています！