Pythonで線形代数!固有値と固有ベクトルを求める

行列の固有値と固有ベクトルは統計学的にも物理学的にも重要な意味を持っており、計算可能な技能を身に着けることは今では技術者として必須の項目といっても過言ではないかも知れません。ここでは計算技能としての手計算と、Pythonによる簡単な解法手段の両方を紹介します。

僕は線形代数の勉強を「中井悦司, 技術者のための線形代数学, 翔泳社※Amazon」でしています。書籍ではプログラミングについては触れていませんが、ここではPythonによるコーディングにフォーカスして学んだ事の実践を行います。
線形代数学の内容について、より理解を深めたい方は本書の購入をすることで、当ブログで紹介するPythonコードの意味がよくわかるようになると思います。

技術者のための線形代数学 大学の基礎数学を本気で学ぶ ［ 中井 悦司 ］

2,860円(11/20 23:21時点)

楽天市場

当ブログでは、基本的に難しい説明は面倒なのでできるだけしないようにし、結果がPythonで簡単に得られることを優先するという方針で進めます！

ちなみに、今回はP35からの内容と関係しています！

固有値と固有ベクトルの概要

固有値と固有ベクトルの意味を見てみよう！

このページをご覧の皆様の中には、Pythonによるコーディングを知りたい人と、固有値と固有ベクトルとはなんぞやという人の両方いらっしゃると思います。

Pythonによるコーディングを知りたい人は目次から後半にジャンプして頂いて、まずはこれから計算する固有値と固有ベクトルについて簡単に説明しておこうと思います。

行列にはベクトルと呼ばれる方向を示す概念があります。そしてベクトルには行列をかけると大きさ（スカラー）と向き（ベクトル）の両方が変化します。これを線形変換と呼びます。

以下の図の(a)が線形変換の例で、\(\vec{x}\)に行列\(A\)をかけた例を示しています。大きさと向きが変わっていますね？

一方(b)はベクトル\(\vec{x}\)に行列\(A\)をかけても、向きは変わらず大きさだけが変わっています。

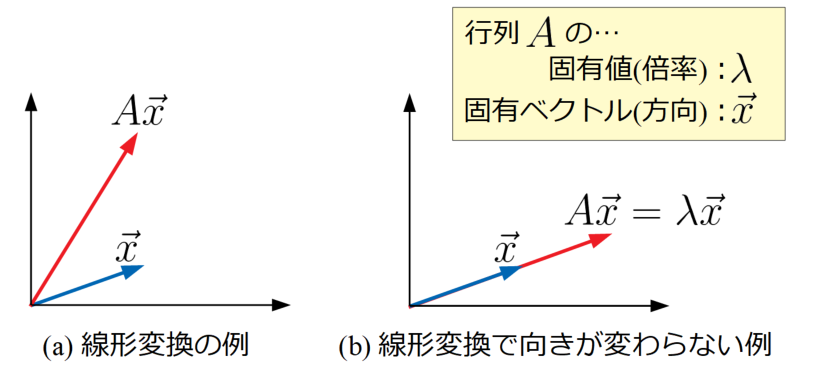
つまり、\(\vec{x}\)に行列\(A\)のをかけたものと、\(\vec{x}\)に定数\(\lambda\)をかけたものはイコールということができます。
この時の\(\lambda\)こそが固有値であり、意味合いとしては倍率になります。

さらに、行列\(A\)にかかっているベクトル\(\vec{x}\)は、向きの変わらない特別なベクトルであるので、これを固有ベクトルと呼びます。

手計算で固有値と固有ベクトルを求めてみよう!

Pythonによるコーディングの前に、固有値と固有ベクトルを手計算で求めてみましょう！

どうも固有値の計算に関する説明は、文章だけでは中々伝わらないと感じています。手計算で求めることによってその意味と大変さを知りましょう！

※Pythonによるコーディングだけ知りたい人は下へスクロールして下さい。

問題とする行列

今回例題として計算する行列は以下の\(A\)です。この行列\(A\)について固有値と固有ベクトルを求めていきます。

\[
A=\begin{bmatrix}
3 &0 \\
1 &2
\end{bmatrix}
\]

固有値を計算する

まず固有値を計算します。

スタートは、上の図中にも書かれている式(1)です。

$$A\vec{x}= \lambda \vec{x}　(1)$$

ここで\(\lambda\)は単なる定数なので、行列\(A\)とサイズが異なります。式(2)に示すように、しれっと行列\(A\)と同サイズの単位行列\(I\)を右辺に入れてみましょう。単位行列はベクトルの左右どちらからかけても構わないという利点があるので、方程式は満たされていますね。

$$A\vec{x}= \lambda I \vec{x}　(2)$$

式(2)を変形させて式(3)を得ます。

$$\left ( A- \lambda I \right ) \vec{x}= \vec{0}　(3)$$

ここで、固有値を求めるためには固有ベクトルが存在しなければいけませんが、固有ベクトルが存在するためには\(\vec{x}\neq\vec{0} \)という条件が定義としてあるため、式(3)の括弧内は正則行列（行列式（det計算）が0にならない行列）でないことが条件になります。

簡単に言うと、式(4)を満たす\(\lambda\)を求めることが固有値を求めることになります。

$$\det\left ( A- \lambda I \right )= 0　(4)$$

では、ここに問題の行列を代入して考えてみましょう。
式(5)が問題の行列を式(4)に代入し、単位行列に\(\lambda\)をかけ、全て成分表示で表したものです。

\[
\det\left ( \begin{bmatrix}
3 &0 \\
1 &2
\end{bmatrix}
-
\begin{bmatrix}
\lambda &0 \\
0 &\lambda
\end{bmatrix} \right )= 0　(5)
\]

式(5)の括弧内減算を計算すると式(6)になり、

\[
\det\left ( \begin{bmatrix}
3-\lambda &0 \\
1 &2-\lambda
\end{bmatrix}
\right )= 0　(6)
\]

det計算をすると、式(7)から式(8)と変形することができます。
この問題は、本当はここまで展開しなくても解はわかりますが、一応式(8)として2×2行列は2次方程式になるということを示しておきます。
この式(8)は特に行列\(A\)の固有方程式と呼ばれます。

$$\left ( 3-\lambda \right )\left ( 2-\lambda \right )-0= 0　(7)$$

$$\lambda ^{2}-5\lambda +6 =0　(8)$$

ここまで出せば、あとは因数分解なり解の公式なりを使って解を求めると、\(\lambda=2, 3\)と二つの解を得ることができます。

この2, 3の両方が固有値です。ここでは便宜上\(\lambda_{1}=2, \lambda_{2}=3\)とします。

固有ベクトルを計算する

続いて固有ベクトルを求めます。

固有値は固有ベクトルがあるという前提で求めていますので、実数解としての固有値が計算された段階で固有ベクトルも存在します。

計算の方法は先ほど求めた二つの固有値\(\lambda_{1}=2, \lambda_{2}=3\)を式(3)にそれぞれ代入し、\(\vec{x}\)を求めるだけです。

\(\lambda_{1}=2\)の場合で書き、\(\vec{x}\)の成分を\(a, b\)と置くと、

\[
\begin{bmatrix}
1 &0 \\
1 &0
\end{bmatrix}\begin{bmatrix}
a\\
b
\end{bmatrix}=
\begin{bmatrix}
0\\
0
\end{bmatrix}
\]

から、この連立方程式を計算すると\(a=0\)という式を得ます。\(b\)については任意の値をとっても構わないという結果とも言えます。

固有ベクトルの意味は方向が変わらないということなので、それさえ維持されていれば大きさは何でも良いとなります。

しかし便宜上、ある値を出したい時は、ベクトルの大きさを1で正規化するということを良くやります。先ほど得られた\(a=0\)は維持してベクトルの大きさ（平方和）が1になる\(b\)は1です。

以上のことから、\(\lambda_{1}=2\)の場合の固有ベクトルは大きさを1で正規化すると[0, 1]であるというのが解答です。

一方、\(\lambda_{2}=3\)の場合は同様に解くと、\(a=b\)となり、これも大きさを1として正規化すると、[\(1/\sqrt{2}, 1/\sqrt{2}\)]と計算されます。

Pythonによる固有値と固有ベクトルを求めるコード

長々と式を描きましたが、Pythonによる固有値と固有ベクトルを求めるコードを以下に示します。

これだけです！

ここで、eigが固有値、vが固有ベクトルを表します。

ちなみに結果は以下の値がコンソールに表示されます。

上の例題と対応をとってみると明白ですが、同一の値が計算されているとわかると思います（\(1/\sqrt{2}\)は分数ではなく、計算後の値ですが）。

PythonのNumPyに入っている線形代数モジュールのeig関数なら一瞬ですね。

本ページで例題として記載した2×2行列であれば手計算でもまだなんとかなりますが、3×3、100×100だと絶望しますよね。実際の工学の世界では、100万×100万行列を扱ったりもするため、コンピュータの助けが無いと一生行列演算する人にもなりかねませんね。

まとめ

本ページでは線形代数学の分野で扱う固有値と固有ベクトルの概要を線形変換から説明し、簡単な2×2行列の手計算で理解を促した後にPythonコードを紹介しました。

Pythonコードであれば面倒な行列演算も一瞬で片付くスマートさであることが実感できたと思います。