
Pythonはシミュレーション系のライブラリパッケージも充実しています。ここでは最も簡単な解析の1つである減衰の無い1自由度のばね質点振動系の自由振動を扱うことで、Pythonを使ったシミュレーションの基礎を学びます。
こんにちは。wat(@watlablog)です。
どうやらPythonを使うとシミュレーションも簡単にコーディングできるみたいです。ここでは多分最も簡単な減衰の無い1自由度の振動系でシミュレーションを学びます。
1自由度非減衰系とは?
1自由度非減衰系とは、ここでは以下の図に示す、1つの質点と1つのばねで構成され、一端が固定拘束されているモデルのことを指します。
各要素はそれぞれパラメータ値を持ちます。
質点要素には質量\(m\)[kg], ばね要素には剛性係数(ばね定数)\(k\)[N/m]という値を物理的に持っています。
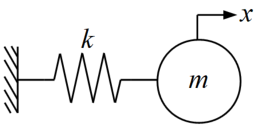
ばね要素だけであれば\(F=kx\)とフックの法則でおなじみで、変位\(x\)が発生すると\(x\)に比例して復元力\(F\)が発生します。
質点要素だけであれば、ニュートンの運動方程式である\(F=ma\)で示され、質量を持つ物体をどんどん速く動かそうと加速度を加えるほどに力が必要とわかります。
上で示したばね要素と質点要素が共に繋がった場合も運動方程式の形式になりますが、以下の式(1)で表現可能です。加速度は\(x\)を使って書いているので微分方程式となります。この式は復元力と慣性力を有するので、振動することが可能です。
右辺は外力項ですが、このページでは外力が働かない自由振動の状態で記述しています。
$$m\ddot{x}+kx=0 (1)$$
この式は変数が1つの線形常微分方程式ですが、変位\(x\)の2階微分\(\ddot{x}\)が入っているので、2階の線形常微分方程式と呼ばれます。
このページではこの2階線形常微分方程式をPythonで解く方法を習得します。
Pythonによる振動シミュレーションのコード
インポートするパッケージ
インポートするパッケージは配列操作のためのNumPyと微分方程式の解法のために積分器を使うのでSciPyからodeintを呼びます。グラフプロットはいつも通りmatplotlibで行います。
|
1 2 3 |
import numpy as np from scipy.integrate import odeint import matplotlib.pyplot as plt |
パラメータの設定
モデルには物理的なパラメータが必要です。質量\(m\)と剛性\(k\)、初期条件state0を設定しています。初期条件は初期変位x0と初期速度v0です。
後半はシミュレーションに必要な時間関係の設定です。
解析をかける初期時間t0と終了時間tf、時間刻みdtを使って時間軸配列tを作成します。このtの時間で解析結果が出力されます。
|
1 2 3 4 5 6 7 8 |
m = 0.5 # 質量[kg] k = 1000 # 剛性[N/m] state0 = [0.0, 0.1] # 初期値[x0, v0] t0 = 0 # 初期時間[s] tf = 1 # 終了時間[s] dt = 0.005 # 時間刻み[s] t = np.arange(t0, tf+dt, dt) # 時間軸配列 |
変数変換で式を変形してodeintを使う
Pythonの常微分方程式を数値的に解くodeintは…というよりExcelVBAでも他の言語でも同じだと思いますが、1階の常微分方程式しか解くことができません。
そのため2階の常微分方程式を1階にする必要があります。
2階の微分方程式を1階にするには、式(2)で変数変換を行います。
\[ \begin{cases}
x_{1}= x \\
x_{2}= \dot{x}
\end{cases} (2)
\]
この変換を行うことで、式(1)は式(3)と書くことができます。
$$m\dot{x_{2}}+kx_{1}= 0 (3)$$
変位\(x\)の2階微分は\(x_{2}\)の1階微分で書くことができるようになったので、\(\dot{x_{2}}\)は式(3)を変形させて式(4)となります。
$$\dot{x_{2}}=-\frac{k}{m}x_{1} (4)$$
以上までをPythonのコードにすると以下のようになります。def文の中には式(4)が書いてあります。
odeint関数にはこのdef文で作った関数、初期値、時間配列の他にargsとしてその他のパラメータをタプル形式で渡します。もしパラメータが1つだけの場合は(a, )のように空欄で指定します。
シミュレーション結果としてsolに入ってくるのは\(x_{1}, x_{2}\)なので変位と速度です。
|
1 2 3 4 5 6 7 8 9 |
# mk system def func(state,t, m, k): x1, x2 = state dx2dt = - (k/m) * x1 return [x2, dx2dt] # odeintを使った解法 # x1, x2の解を求めているので、sol[0]が変位x1, sol[1]が速度x2となる sol = odeint(func, state0, t, args=(m,k)) |
グラフ設定と理論値との比較
今回初めての数値計算ということで、理論値との比較を行います。本モデルは解に振動現象を仮定して、オイラーの公式を使うと以下の式(5)の解を得ます。
$$x= x_{0}cos\omega t+\frac{v_{0}}{\omega }sin\omega t (5)$$
ちなみに速度は式(5)を微分して式(6)として表現可能です。
$$\dot{x}= -x_{0}\omega sin\omega t+v_{0}cos\omega t (6)$$
ここで\(\omega\)は式(7)で示す固有角振動数です。
$$\omega= \sqrt{\frac{k}{m}} (7)$$
理論値とグラフプロットは以下のコードに示します。このコードは速度比較として書いています。変位を比較する場合はplotの部分をsol[:, 0]に変更し、theoryを式(5)に変更して下さい。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 |
omega = np.sqrt(k/m) theory = (-1 * state0[0] * omega * np.sin(omega * t)) +\ (state0[1] * np.cos(omega * t)) # ここからグラフ描画 # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure() ax1 = fig.add_subplot(111) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('Time [s]') ax1.set_ylabel('Velocity [m/s]') # データの範囲と刻み目盛を明示する。 ax1.set_xticks(np.arange(0, 2, 0.2)) ax1.set_yticks(np.arange(-1, 1, 0.1)) ax1.set_xlim(0, 1) ax1.set_ylim(-0.2, 0.2) # データプロット ax1.plot(t, sol[:,1], label='Python odeint [x0=0, v0=0.1]', c='b', marker='o', linestyle='None') ax1.plot(t, theory, label='Theory', c='r') fig.tight_layout() plt.legend(loc='upper left') # グラフを表示する。 plt.show() plt.close() |
実行結果
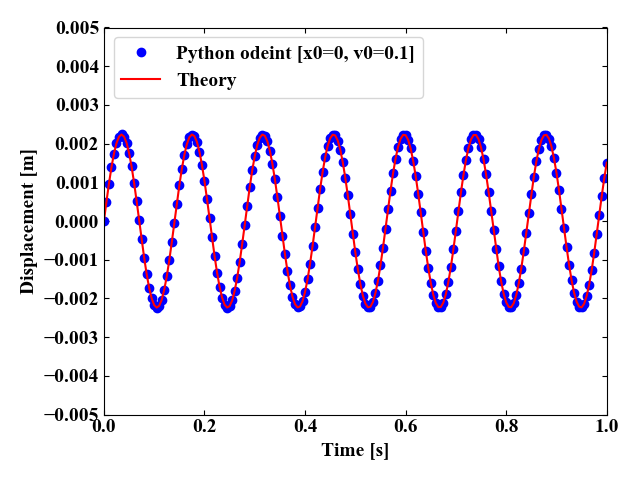
以下が実行結果です。非減衰モデルの単振動なので、自由振動といっても一度振動すると止まらず振動し続けます。
以下は変位\(x\)のPythonによる数値計算結果と理論値を比較した結果です。双方のプロットが重なっていることから、本計算結果は正しいと言うことができそうですね。
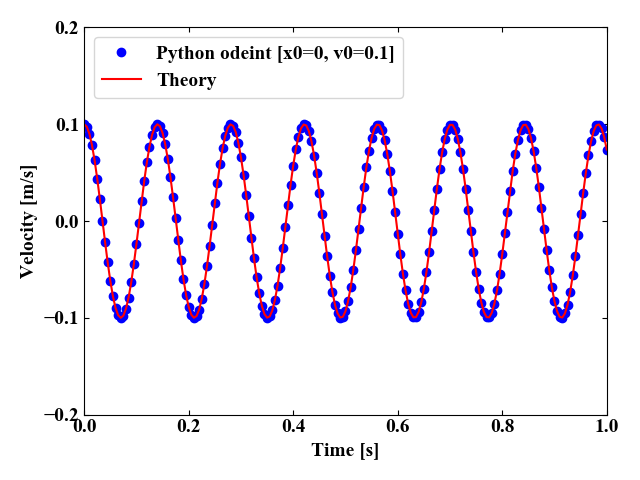
続いて速度です。こちらも理論値と比べて大きく違う所は無いです。このシミュレーションは関数部分と実行部分で実質5行くらいがメインなので、こんなに簡単にコーディングできるのは素晴らしいですね。
まとめ
本ページでは1自由度非減衰系のモデルについて概要を説明しました。
振動モデルは2階の線形常微分方程式ですが、Pythonのodeintを使うために変数変換という手法を用いて1階の線形常微分方程式にして解きました。
解いた結果を理論値と比較し、数値計算結果と重なることを確認しました。
今回は最も簡単なシミュレーションの1つである減衰の無い1自由度の振動モデルを扱いました!odeintの他にもルンゲクッタを使えるodeという関数もあるようですので、そのうち使ってみようと思いました。
Twitterでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています!
全コード
コピペがしやすいように、全コードを以下にまとめました。是非お持ちの環境で実行してみて下さい。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 |
import numpy as np from scipy.integrate import odeint import matplotlib.pyplot as plt # mk system def func(state,t, m, k): x1, x2 = state dx2dt = - (k/m) * x1 return [x2, dx2dt] m = 0.5 # 質量[kg] k = 1000 # 剛性[N/m] state0 = [0.0, 0.1] # 初期値[x0, v0] t0 = 0 # 初期時間[s] tf = 1 # 終了時間[s] dt = 0.005 # 時間刻み[s] t = np.arange(t0, tf+dt, dt) # 時間軸配列 # odeintを使った解法 # x1, x2の解を求めているので、sol[0]が変位x1, sol[1]が速度x2となる sol = odeint(func, state0, t, args=(m,k)) omega = np.sqrt(k/m) theory = (state0[0] * omega * np.cos(omega * t)) +\ ((state0[1]/omega) * np.sin(omega * t)) # ここからグラフ描画 # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure() ax1 = fig.add_subplot(111) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('Time [s]') ax1.set_ylabel('Displacement [m]') # データの範囲と刻み目盛を明示する。 ax1.set_xticks(np.arange(0, 2, 0.2)) ax1.set_yticks(np.arange(-1, 1, 0.001)) ax1.set_xlim(0, 1) ax1.set_ylim(-0.005, 0.005) # データプロット ax1.plot(t, sol[:,0], label='Python odeint [x0=0, v0=0.1]', c='b', marker='o', linestyle='None') ax1.plot(t, theory, label='Theory', c='r') fig.tight_layout() plt.legend(loc='upper left') # グラフを表示する。 plt.show() plt.close() |

 ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!
ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!
コメント