Pythonで画像処理をする時に、平面に画像を貼り付けて動かすことを考えます。その場合、やみくもに座標を模索するのではなく、数学的に関数を使う方がスムーズに動きます。ここでは楕円方程式を使って平面が回転しているような動きを表現してみます。
こんにちは。wat(@watlablog)です。画像処理は数学の関数と組み合わせると良さそうです。ここでは楕円方程式を使って平面をくるくるさせるプログラムを習得します！
平面を回転させる効果を楕円方程式で表現する
平面が回転しているように見える動画
以下のGIF動画が平面が回転して見える効果を狙ったものです。四角形が反時計回りに、3次元的にくるくると回っているように見えると思います。
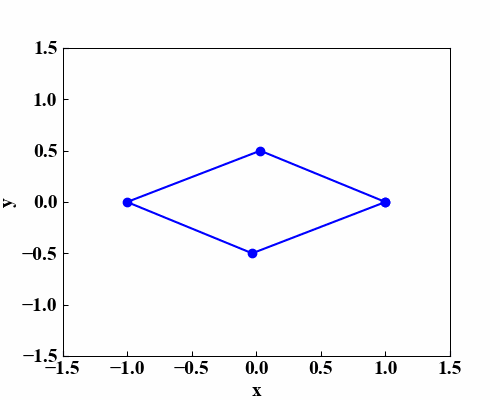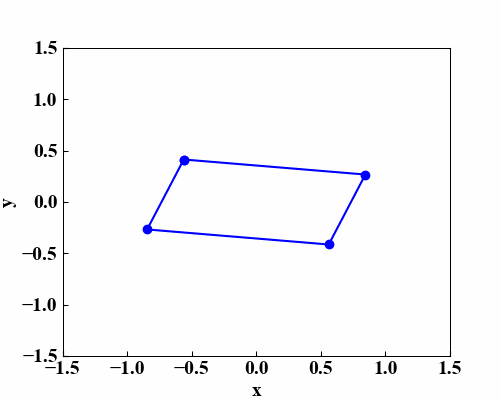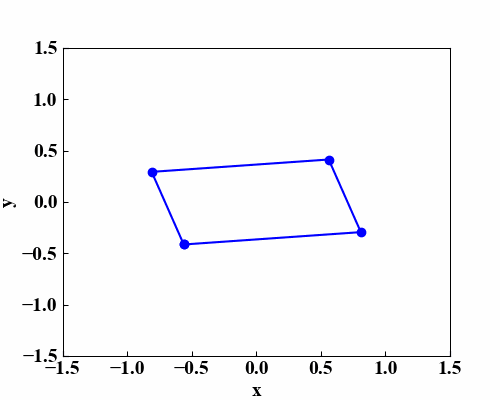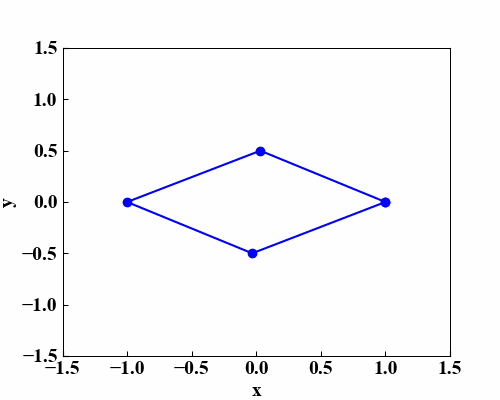
これは「Python/NumPyで楕円方程式を描画する！」で作成した楕円方程式の関数と、「Pythonのmatplotlibアニメーションで楕円の軌跡！」で習得したmatplotlibを使ったアニメーション作成関数を使って作っています。
上記記事では1点だけを使ってアニメーションをさせていましたが、今回は4点使ったアニメーションについて記載します。
Pythonによる平面回転アニメーション作成プログラム
楕円関数に工夫を加える
今回は1点ではなく4点同時に楕円方程式の\(x\)と\(y\)を計算する必要があります。楕円方程式は前回紹介したように以下の式で\(y\)値を求めます。
$$y=\pm b\sqrt{1-\frac{x^{2}}{a^{2}}}$$
この式は±のある式なので、同一\(x\)で二値を取り、符号調整が必要でした。1点だけの時はこの符号調整は簡単だったのですが、4点の時はそれぞれ別々に符号を調整する必要があります。
以下に楕円方程式の関数を示します。ここでcが符号調整のためのスイッチの役割をしていますが、1点の時は初期値が1だったのに対して、今回はiniという変数を使っています。これだけで全点の符号調整を行います。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
def ellipse(x, a, b, g, ini): y = [] # y値をためる c = ini # y軸の符号スイッチ # 第1象限から第4象限までの全てのy値を計算 for i in range(len(g)): y_single = b * np.sqrt(1 - (np.power(x[i], 2) / np.power(a, 2))) if i == 0: pass elif np.sign(g[i - 1]) == np.sign(g[i]): pass else: c = -1 * c y.append(y_single * c) # y値の符号調整 return y |
パラメータ設定
楕円方程式のパラメータやアニメーションフレーム数を設定した後に、\(x\)の振動範囲を決めるtを用意します。
ここで、第1象限と第2象限にある点はπから－πに向かって動くのに対して、第3象限と第4象限にある点は－πからπ方向に動くため、tとt_invを用意しています。
位相phaseは4点の位置関係を示します。この値によって四角形の形が台形になったりひし形になったりします。
|
1 2 3 4 5 6 7 8 |
a = 1.0 # 楕円方程式のa b = 0.5 # 楕円方程式のb N = 30 # フレーム分割数 t = np.linspace(-1 * np.pi, np.pi, N) # －π～πまでの範囲 t_inv = np.linspace(np.pi, -1 * np.pi, N) # π～－πまでの範囲 # 位相配列 phase = [np.pi/2, np.pi/100, -1 * np.pi/2, -1 * np.pi/100] |
勾配を計算する
1点の時と違い、4点の場合はtとt_invを使う2パターンずつ勾配を決める必要がありますので、場合分けにif文を使っています。そのため、\(x, g\)は共に配列になります。
4点分あるのでforループを使っています。
|
1 2 3 4 5 6 7 8 9 |
# 楕円方程式中で振動させるxとy値の符号判断用に勾配を計算する x = [] g = [] for i in range(4): if i <= 1: x.append(a * np.sin(t - phase[i])) else: x.append(a * np.sin(t_inv - phase[i])) g.append(np.gradient(x[i])) |
楕円方程式のy値を計算する
\(y\)も同様にif文で場合分けをしていますが、これは先ほど紹介した符号調整変数cの初期値が1か－1かを分けています。
こちらも4点分あるのでforループを使っています。
|
1 2 3 4 5 6 7 |
# 楕円方程式のy値を計算する y = [] for j in range(4): if j <= 1: y.append(ellipse(x[j], a, b, g[j], 1)) else: y.append(ellipse(x[j], a, b, g[j], -1)) |
アニメーション
続いてアニメーションとグラフプロットのコードを以下に示します。アニメーションは1点ずつ動く様子をフレーム毎にためていく必要があるので、これもforループを使っています。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 |
# 4つのプロットを同時にアニメーションさせるための準備 imgs = [] fig = plt.figure(figsize = (5, 4)) # プロットにためる前にfigureを作っておく x = np.array(x) y = np.array(y) for k in range(len(t)): X = [] Y = [] for l in range(4): X.append(x[l, k]) Y.append(y[l, k]) # グラフ描画 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' plt.xlabel('x') plt.ylabel('y') plt.xticks(np.arange(-2, 2, 0.5)) plt.yticks(np.arange(-2, 2, 0.5)) plt.xlim(-1.5, 1.5) plt.ylim(-1.5, 1.5) img = plt.plot(X, Y, c='b', marker='o', linestyle='None') imgs.append(img) # アニメーションを作ってgifファイルに保存する ani = animation.ArtistAnimation(fig, imgs, interval=10) ani.save('ellipse-course.gif', writer='pillow', fps=30) # プロットを表示させる plt.show() plt.close() |
これらのコードを実行すると、以下のGIF画像が作成されます。上の動画みたいに線を付ける場合はもう1点追加したり特殊なことをしなければいけませんが、この後画像を動かすことを考えたらこの状態の方が扱いやすいので線は描きません。
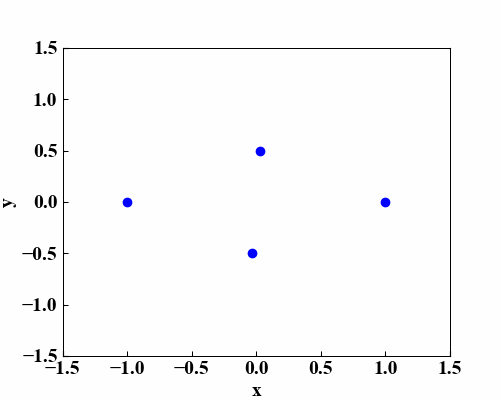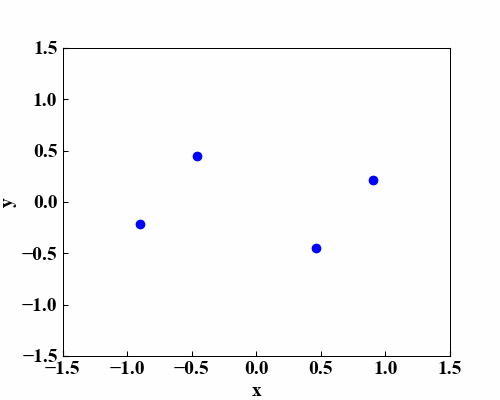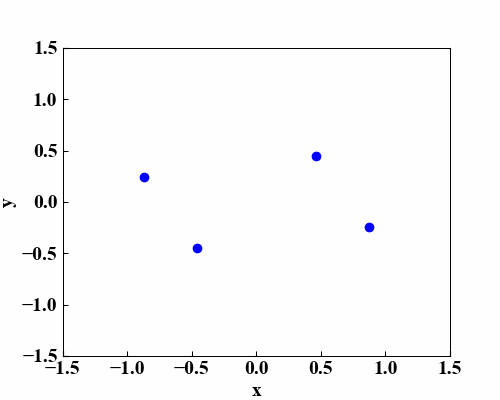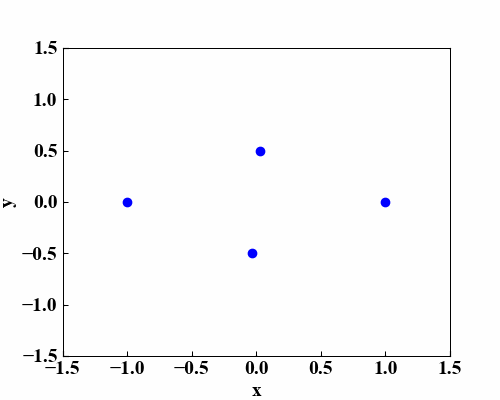
まとめ
楕円方程式とmatplotlibのアニメーションを使って平面が回転しているような効果を狙ったプロットをしてみました。
次回はいよいよ画像にこのコードを適用してみます。
実際は2次元空間内を点が移動しているだけですが、楕円方程式を使うことであたかも3次元空間に平面があるかのような効果を出すことができました！
Twitterでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています！
全コード
コピペがしやすいように、上で分割記載しているコードを1つにまとめてみました。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 |
import numpy as np from matplotlib import pyplot as plt from matplotlib import animation def ellipse(x, a, b, g, ini): y = [] # y値をためる c = ini # y軸の符号スイッチ # 第1象限から第4象限までの全てのy値を計算 for i in range(len(g)): y_single = b * np.sqrt(1 - (np.power(x[i], 2) / np.power(a, 2))) if i == 0: pass elif np.sign(g[i - 1]) == np.sign(g[i]): pass else: c = -1 * c y.append(y_single * c) # y値の符号調整 return y a = 1.0 # 楕円方程式のa b = 0.5 # 楕円方程式のb N = 30 # フレーム分割数 t = np.linspace(-1 * np.pi, np.pi, N) # －π～πまでの範囲 t_inv = np.linspace(np.pi, -1 * np.pi, N) # π～－πまでの範囲 # 位相配列 phase = [np.pi/2, np.pi/100, -1 * np.pi/2, -1 * np.pi/100] # 楕円方程式中で振動させるxとy値の符号判断用に勾配を計算する x = [] g = [] for i in range(4): if i <= 1: x.append(a * np.sin(t - phase[i])) else: x.append(a * np.sin(t_inv - phase[i])) g.append(np.gradient(x[i])) # 楕円方程式のy値を計算する y = [] for j in range(4): if j <= 1: y.append(ellipse(x[j], a, b, g[j], 1)) else: y.append(ellipse(x[j], a, b, g[j], -1)) # 4つのプロットを同時にアニメーションさせるための準備 imgs = [] fig = plt.figure(figsize = (5, 4)) # プロットにためる前にfigureを作っておく x = np.array(x) y = np.array(y) for k in range(len(t)): X = [] Y = [] for l in range(4): X.append(x[l, k]) Y.append(y[l, k]) # グラフ描画 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' plt.xlabel('x') plt.ylabel('y') plt.xticks(np.arange(-2, 2, 0.5)) plt.yticks(np.arange(-2, 2, 0.5)) plt.xlim(-1.5, 1.5) plt.ylim(-1.5, 1.5) img = plt.plot(X, Y, c='b', marker='o', linestyle='None') imgs.append(img) # アニメーションを作ってgifファイルに保存する ani = animation.ArtistAnimation(fig, imgs, interval=10) ani.save('ellipse-course.gif', writer='pillow', fps=30) # プロットを表示させる plt.show() plt.close() |