画像処理でグラフィカルなアニメーションを作ったりする場合、軌跡の座標点に円や楕円方程式を使いたくなる場合があります。楕円は円の拡張なので、ここでは楕円方程式の描画をやってみます。
こんにちは。wat(@watlablog)です。
画像処理関連で色々やりたく、その前段階で楕円を扱いたくなったので、ここでは楕円方程式の描画をやってみます！
楕円方程式をPythonで描画する
楕円方程式
今回は\(y\)軸上に焦点のある楕円方程式を扱います。楕円方程式は以下の式で表すことができます。
$$\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1$$
\(y\)について整理すると、以下の式になります。\(x\)の値によっては2値をとるので、±が付いていますね。
$$y=\pm b\sqrt{1-\frac{x^{2}}{a^{2}}}$$
楕円方程式のパラメータと円の形
ここで\(a\)と\(b\)の値が楕円の潰れ具合を決めるパラメータです。\(a=b\)の時は真円となりますが、等しくない場合は以下の図のように潰れ方が変わります。
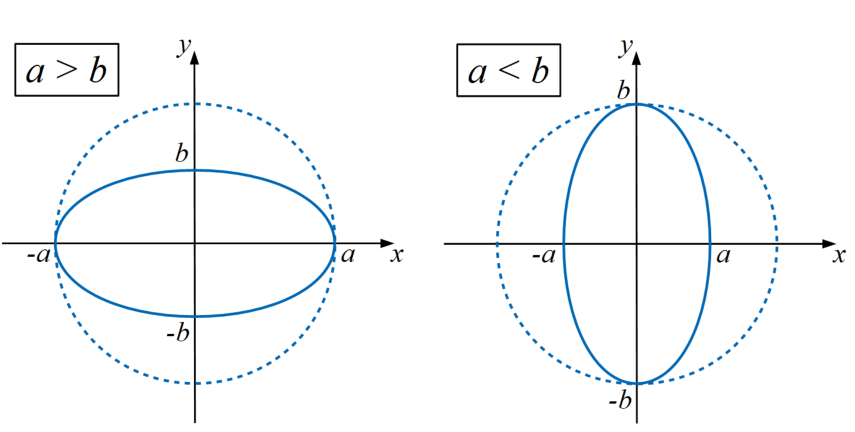
今回はこれをグラフ描画してみます。
Pythonコード
インポートするパッケージ
import文でインポートするパッケージはNumPyとmatplotlibです。
|
1 2 |
import numpy as np from matplotlib import pyplot as plt |
楕円方程式の関数を作る
楕円方程式の関数は、先に紹介した式をdef文で作っておきます。
|
1 2 3 |
def ellipse(x, a, b): y = b * np.sqrt(1 - (np.power(x, 2) / np.power(a, 2))) return y |
軸とパラメータを作る
楕円方程式中の\(a, b\)を定義します。また、円は第1象限から第4象限まで、形こそ相似ですが符号が異なります。今回は後の画像処理で使えるように全範囲の\(x\)の値と\(y\)の値をセットで手に入れたい（さらに順番も円の軌跡を描けるように）ので一工夫しています。
まず\(t\)として±πの範囲の軸を作ります。
次に位相phaseと振幅\(a\)を考慮して\(x\)を\(t\)を使って表現することで、楕円方程式の\(x\)軸を、\(-a\)から\(a\)の範囲で作成します。
np.gradientで勾配\(g\)を作成しているのは、符号の変化を判別する時に使います。
|
1 2 3 4 5 6 |
a = 1.0 # 楕円方程式のa b = 0.5 # 楕円方程式のb t = np.linspace(-1 * np.pi, np.pi, 100) # －π～πまでの範囲 phase = np.pi / 2 # 位相 x = a * np.sin(t - phase) # 1周期分の正弦波を作成 g = np.gradient(x) # xの勾配を計算 |
全象限の値を計算する
勾配の符号が変化したタイミングで\(y\)の値を符号変換（-1をかける）することで、\(x\)が折り返した時にスムーズに円を描く軌跡をとります。
|
1 2 3 4 5 6 7 8 9 10 |
# 第1象限から第4象限までの全てのy値を計算 y = [] for i in range(len(g)): y = np.append(y, ellipse(x[i], a, b)) if i == 0: pass elif np.sign(g[i-1]) == np.sign(g[i]): pass else: y = -1 * y |
グラフの設定
最後にグラフの設定です。正直ここは単純にプロットするだけでも十分ですが、ちょっと見た目にこだわったためグラフ設定が長くなってしまいました。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 |
# ここからグラフ描画 # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure() ax1 = fig.add_subplot(111) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('x') ax1.set_ylabel('y') # データの範囲と刻み目盛を明示する。 ax1.set_xticks(np.arange(-2, 2, 0.5)) ax1.set_yticks(np.arange(-2, 2, 0.5)) ax1.set_xlim(-1, 1) ax1.set_ylim(-1, 1) # データプロットの準備とともに、ラベルと線の太さ、凡例の設置を行う。 ax1.plot(x, y, label='ellipse', lw=1) ax1.set_aspect('equal') fig.tight_layout() # グラフを表示する。 plt.show() plt.close() |
実行結果
上記コードを全て貼り付け実行すると以下の結果が得られます。楕円を描くことができました。
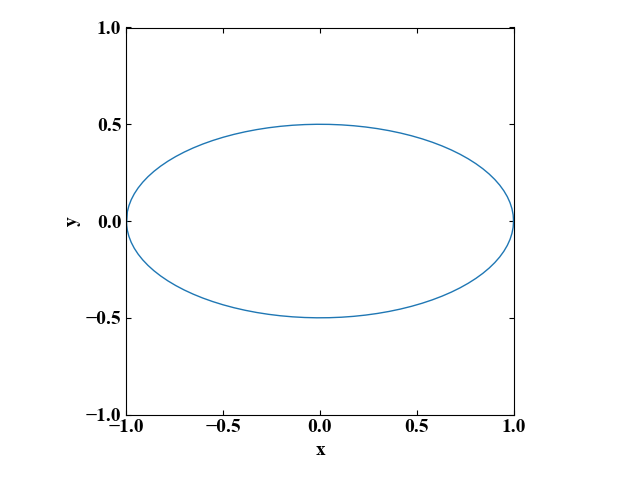
まとめ
本ページでは楕円方程式の紹介と、Pythonによる描画コーディングを紹介しました。
今回はやってみた回です。後で画像処理でグラフィカルにアニメーションを作ることをやりたくて、楕円方程式を描画しました。
ただ単に描画するだけであれば、\(x, y\)が共に正の時の値だけを計算しておいて、符号を入れかえれば良いのですが（位相の考慮もせず）、今回はあえて全象限の座標を計算しました。
後程画像処理のカテゴリで結果を紹介したいと思います。
今回はあえて全ての範囲の楕円方程式の座標を計算しました。その目的は後程。
Twitterでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています！
コメント