
勾配降下法に代表される最適化手法には様々な手法があります。ここではAdaGradの弱点を改善するRMSPropの概要を説明し、PythonのNumpyで実装、他の手法と比較してみます。
こんにちは。wat(@watlablog)です。ここでは機械学習最適化手法の1つ、RMSPropを学習していきます!
RMSPropの概要
RMSPropに至るまでの変遷
この記事を読んでいる方はおそらく勾配降下法がどんなものか、MomentumやAdaGradがどんなものかある程度把握している方と予想します。RMSPropもこれら機械学習で使われる最適化手法の1つです。
まだこれらの手法が曖昧な方は、是非以下の3つの記事を順番に読んでみて下さい。それぞれの最適化手法のメリットとデメリットを知ると、このページで学ぶRMSPropの改善点がより理解できると考えられます。
①「Pythonで1変数と2変数関数の勾配降下法を実装してみた」
②「勾配降下法に慣性項を追加するMomentumをPythonで実装」
③「Python/Numpyで機械学習の最適化!AdaGradを実装」
①の記事は基本中の基本となる勾配降下法(GD)の内容です。非常にシンプルな式で関数の勾配を下っていく有名な手法です。この勾配降下法は機械学習以外の様々な分野で使われていますが、緩やかな勾配にさしかかった途端に学習が遅くなるというデメリットがありました。
②はMomentumという勾配降下法の式に慣性項を追加した手法です。Momentumは前の更新情報を現在の値の更新にも使うので、あたかも運動方程式中の質点のような振る舞いをします。しかし、その学習率は重みにかかわらず一定で、さらにハイパーパラメータが2つ必要で調整が困難というデメリットがありました。
③はAdaGradという手法で、それぞれの重みに適応させた学習率になるように勾配降下法の更新式を変更した画期的な発想を持っていました。しかし学習が進むにつれ更新量がどんどん小さくなっていき、場合によっては学習が全くされない状況となるデメリットを持っていました。
RMSPropはAdaGradの改善を狙った手法で、過去の情報を「忘れる」というコンセプトを持っています(RMSPropはCouseraの講義でヒントン氏が提案した手法で、正式に論文はないとか?)。
RMSPropの更新式とメリット
RMSPropの更新式を式(1)、式(2)に示します。
$$\mathbf{h}_{i+1}=\rho \mathbf{h}_{i}+ (1 - \rho)( \nabla f)^{2} (1)$$
$$\mathbf{x}_{i+1}=\mathbf{x}_{i}-\eta \frac{1}{\sqrt{\mathbf{h}_{i+1}}} (\nabla f) (2)$$
こうしてみると、最終的な更新式である式(2)はAdaGradと全く同じですが、式(1)の\(\mathbf{h}\)の更新式が異なります。
式(1)は\(\rho\)の存在(\(\rho\)は1より小さい値(ヒントン氏は0.9を推奨))により前回の更新量を小さくする方向に働きます。
AdaGradはどんどん更新量が小さくなっていきますが、RMSPropは適度な\(\rho\)を設定することにより更新量が小さくなり過ぎないような改善を狙っています。
RMSPropをその他手法と比較するコード
全コード
先ほど紹介した3記事と同じコードなので詳細な説明は省きますが、このRMSPropをGD、Momentum、AdaGradの下に追記しました。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 |
import numpy as np from matplotlib import pyplot as plt from mpl_toolkits.mplot3d import Axes3D # グラフプロット用基準関数 def f(x, y): z = (1/4) * x ** 2 + y ** 2 return z # 基準関数の微分 def df(x, y): dzdx = (1/2) * x dzdy = 2 * y dz = np.array([dzdx, dzdy]) return dz # 共通のパラメータ max_iteration = 50 # 最大反復回数 eta = 0.1 # 学習率 # GDのパラメータ x0_gd = -10 y0_gd = 10 x_gd = [x0_gd] y_gd = [y0_gd] # Momentumのパラメータ alpha = 0.5 x0_mom = -10 y0_mom = 10 x_mom = [x0_mom] y_mom = [y0_mom] pre_update = np.array([0, 0]) # AdaGradのパラメータ eta_adagrad = 2 x0_adagrad = -10 y0_adagrad = 10 x_adagrad = [x0_adagrad] y_adagrad = [y0_adagrad] h0 = np.array([0, 0]) # RMSpropのパラメータ eta_rms = 2.0 ro = 0.9 x0_rms = -10 y0_rms = 10 x_rms = [x0_rms] y_rms = [y0_rms] h0_rms = np.array([0, 0]) # 最大反復回数まで計算する for i in range(max_iteration): # GDの更新 x0_gd, y0_gd = np.array([x0_gd, y0_gd]) - eta * df(x0_gd, y0_gd) x_gd.append(x0_gd) y_gd.append(y0_gd) # Momentumの更新 update = eta * df(x0_mom, y0_mom) + alpha * pre_update x0_mom, y0_mom = np.array([x0_mom, y0_mom]) - update pre_update = update x_mom.append(x0_mom) y_mom.append(y0_mom) # AdaGradの更新 h0 = h0 + df(x0_adagrad, y0_adagrad) ** 2 x0_adagrad, y0_adagrad = np.array([x0_adagrad, y0_adagrad]) - eta_adagrad\ * (1 / (np.sqrt(h0)+1e-7)) * df(x0_adagrad, y0_adagrad) x_adagrad.append(x0_adagrad) y_adagrad.append(y0_adagrad) # RMSPropの更新 h0_rms = ro * h0_rms + (1 - ro) * df(x0_rms, y0_rms) ** 2 x0_rms, y0_rms = np.array([x0_rms, y0_rms]) - eta_rms \ * (1 / np.sqrt(h0_rms)) * df(x0_rms, y0_rms) x_rms.append(x0_rms) y_rms.append(y0_rms) print(i) # 軌跡描画用計算 x_gd = np.array(x_gd) y_gd = np.array(y_gd) z_gd = f(x_gd, y_gd) x_mom = np.array(x_mom) y_mom = np.array(y_mom) z_mom = f(x_mom, y_mom) x_adagrad = np.array(x_adagrad) y_adagrad = np.array(y_adagrad) z_adagrad = f(x_adagrad, y_adagrad) x_rms = np.array(x_rms) y_rms = np.array(y_rms) z_rms = f(x_rms, y_rms) # 基準関数の表示用 x = np.arange(-10, 11, 2) y = np.arange(-10, 11, 2) X, Y = np.meshgrid(x, y) Z = f(X, Y) # ここからグラフ描画---------------------------------------------------------------- # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # グラフの入れ物を用意する。 fig = plt.figure() ax1 = Axes3D(fig) # 軸のラベルを設定する。 ax1.set_xlabel('x') ax1.set_ylabel('y') ax1.set_zlabel('z') ax1.view_init(elev=60, azim=-30) # データプロットする。 ax1.plot_wireframe(X, Y, Z, label='f(x, y)') ax1.scatter3D(x_gd, y_gd, z_gd, label='GD', color='blue', s=50) ax1.scatter3D(x_mom, y_mom, z_mom, label='Momentum', color='red', s=50) ax1.scatter3D(x_adagrad, y_adagrad, z_adagrad, label='AdaGrad', color='green', s=50) ax1.scatter3D(x_rms, y_rms, z_rms, label='RMSProp', color='yellow', s=50) # グラフを表示する。 plt.legend() plt.show() plt.close() |
実行結果
以下が実行結果です。
…GDやMomentumと比べるとAdaGradやRMSPropは降下方向が違うので、重みそれぞれに適応しているというのがわかりますが、静止画だとAdaGradとRMSPropの違いはいまいちわかりませんね。

しかし動画にすると一目瞭然でした。同じ学習率を設定していますが、AdaGradが慎重に降下している最中にRMSPropがダントツでゴールに到達しました。
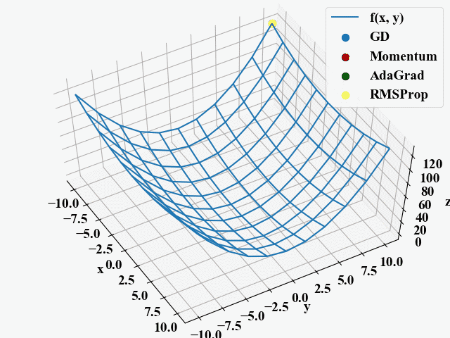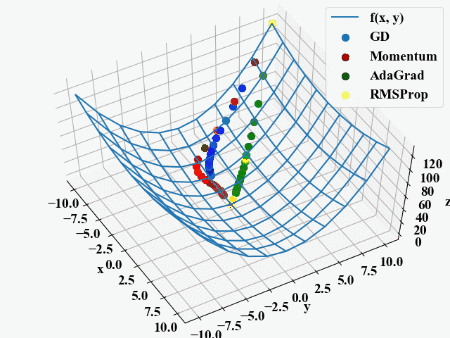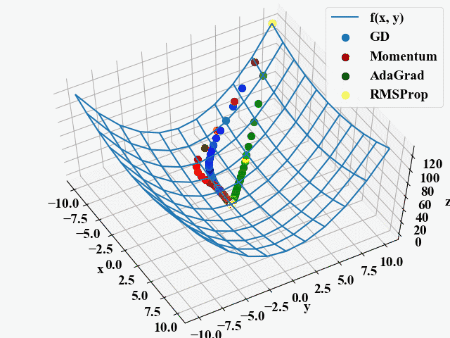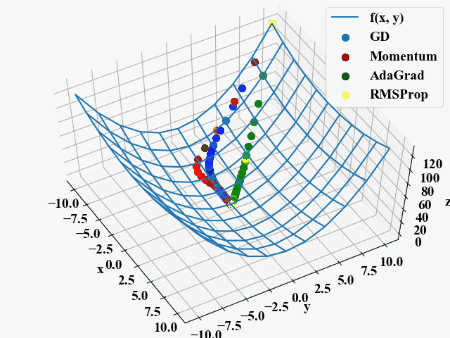
\(\rho\)が入っているだけでこの違い。流石ヒントンさん。
まとめ
本ページでは最適化手法のRMSPropを試してみました。
RMSPropは「忘れる」ということを式の中で表現したユニークな適応的降下法で、Numpyで書いたコードでもAdaGradと比べると改善傾向が見られました。
ちょっとした式変化でこんなに挙動が変わるということに毎回驚かされます!
Twitterでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています!

 ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!
ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!
コメント