
機械学習や数値解析で頻繁に用いられる勾配降下法は最適化問題に解を与える有力手法です。ここではアルゴリズムを理解するために、最も単純な1変数関数と2変数関数における勾配降下法の実装を学習します。
こんにちは。wat(@watlablog)です。今回は最適化問題でよく使われる勾配降下法をPythonで実装し、簡単な問題を解いてみます!
勾配降下法の概要とキーポイント
勾配降下法とは?
勾配降下法(GD:Gradient Descent)とは、勾配情報から任意関数の最小値を求める問題に使われる手法です。
機械学習でモデルの学習中に教師データとの誤差を最小にしたい時や、ものづくりのシミュレーションで強度やコストといった複数のパラメータを設計する際に使われることがよくあります。
勾配降下法の概念は下図のような坂道に置いたピンポン玉で例えることが可能です。
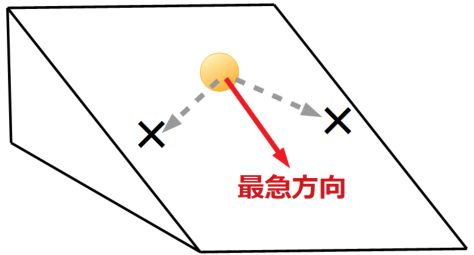
勾配降下法は分野によっては最急降下法(Steepest descent)と呼ばれ、その名の通り最も急な坂道を降りるアルゴリズムをとります。
上図の坂道に置いたピンポン玉は、重力が下方向だとすると×印の付いた方向ではなく、赤矢印で描いた最急方向へ転がります。
この図は僕達人間にとって自明ですが、コンピュータにとっては降りるべき方向を数学的に示してあげる必要があります。
ここでは簡単な数学を使って降りるべき方向を式で表現し、Pythonで実装する所までを扱います。
関数の最小値を反復計算で求める理由
勾配降下法は関数の最小値を計算により求めることを目的としますが、関数を\(f(x)\)とおけば、その最小値と言えば下図のように微分した結果が0(\({f}'(x)=0\))になれば良いということが思いつきます。
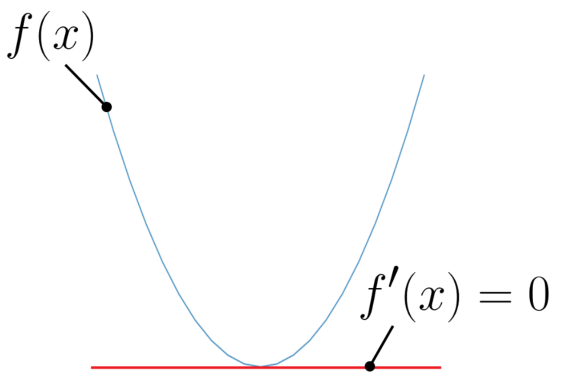
勾配降下法を使わなくても関数の最小値なら求めることができそうだけど?
上の1変数関数であれば微分可能であれば解くことができます。わざわざ反復計算をするアルゴリズムを持ち出す必要はありませんね。
続いて、以下のような2変数関数\(f(x,y)\)はどうでしょうか?
この関数は曲面で表現することができます。
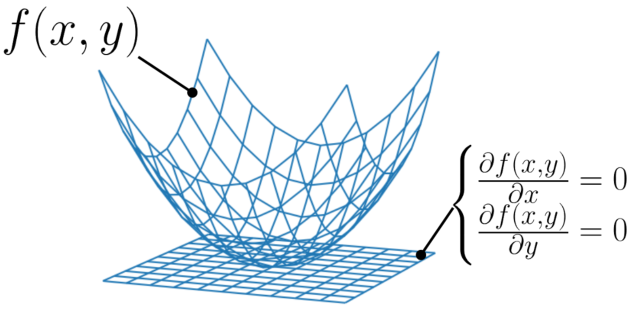
図中にもありますが、2変数関数の場合は関数\(f(x,y)\)を各変数で偏微分し、それぞれが0となる連立方程式を解けば求めることが出来ます。
偏微分とは、微分する変数以外を定数とみなして通常の微分と同じことを行うだけなので、2変数関数は特に理解しやすいでしょう。
そして図示はできませんが、多変数関数でも同じなので最小値を求める方法は一般化されています。
しかし、機械学習、特にディープラーニングで求められる何万、何十万個の変数からなる関数はどうでしょう。
変数の数が多ければ多いほど連立方程式を解くのは困難(コンピュータでも時間がかかる)になってきます。そんな時、手探りで最小値を探していく手法が勾配降下法なのです。
勾配降下法の基礎式
1変数の場合
上の放物線のような1変数関数の場合から勾配降下法の式を見ていきましょう。
1変数の場合の勾配降下法は式(1)で表現されます。
$$x_{i+1}=x_{i}-\eta {f}'(x_{i}) (1)$$
ここで、\(x_{i}\)は現在の値(最初は初期値)を意味し、\(x_{i+1}\)は次の値です。微分した関数に現在の値を入れるということは傾き、すなわち勾配を算出しているということです。
勾配にかかっている\(\eta\)(イータ)は学習率(ゲインとも呼ぶ)で、勾配の情報からどれだけの量で値を更新するかを決めるハイパーパラメータ(エンジニアが事前に決めておくパラメータ)です。
通常\(\eta\)は0.1や0.01といった1より小さな値を使用します。
せっかちな人は\(\eta\)を大きくしがちですが、最小値をうまく探せない可能性があります。逆に心配性な人は\(\eta\)を小さくしがちですが、時間がかかって最小値に辿り着けない場合があります。難しいですね。
2変数関数の場合
次は先ほどの曲面のような2変数関数の場合です。
2変数関数の場合の勾配降下法は式(2)で表現されます。
1変数と同じですが、左辺は次の値が二つあるのでベクトル形で書いています。右辺の括弧内も偏微分したもののベクトルになっています。
この式は現在の値を使って\(x\)と\(y\)をそれぞれどの方向にどれだけ動かせば良いかを意味しています。
多変数関数の場合(一般化)
多変数関数への拡張は2変数関数の式がわかれば容易です。
しかし多くの変数を導入した時、式に書くのが非常に面倒になります。
そのため変数ベクトル\(\mathbf{x}\)(式(3))とハミルトン演算子と呼ばれる\(\nabla\)(ナブラ)記号を用いて勾配を意味する\(\nabla f\)(式(4))を用いると、多変数関数の場合の勾配降下法は式(5)と書くことが可能です。
$$\mathbf{x}=(x, y, z,\cdots ) (3)$$
$$\nabla f=(\frac{\partial f}{\partial x},\frac{\partial f}{\partial y},\frac{\partial f}{\partial z},\cdots ) (4)$$
$$\mathbf{x}_{i+1}=\mathbf{x}_{i}-\eta \nabla f (5)$$
これら一連の式では勾配ベクトルに学習率をかけ、さらに負のベクトルにしています。なぜ負になるのか、なぜこの式で勾配降下法が書けるのかは以下の参考書に書いてあります(P89あたりから)。
Pythonによる勾配降下法コードの実装
1変数関数の勾配降下法コード
全コード
ここからPythonで勾配降下法を実装していきます。特に便利なライブラリというものが見当たらなかったので、基本のnumpyだけを使って実装し、matplotlibで可視化するという段取りです。
基準とする関数は式(6)で、その導関数は式(7)です。今回は最も簡単な放物線の式でコードを試してみます。
$$y=x^{2} (6)$$
$$\frac{\mathrm{d} y}{\mathrm{d} x}=2x (7)$$
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 |
import numpy as np from matplotlib import pyplot as plt # グラフプロット用基準関数 def f(x): y = x ** 2 return y # 基準関数の導関数 def df(x): dy = 2 * x return dy # 勾配降下法に必要なパラメータ eta = 0.1 # 学習率 max_iteration = 1000 # 最大反復回数 x0 = 10 # 初期値 x_pred = [x0] # 描画用軌跡リスト(初期値をプリセット) # 最大反復回数まで計算する for i in range(max_iteration): x0 = x0 - eta * df(x0) # 勾配降下法 x_pred.append(x0) # 軌跡をリストに追加 print(i, x0) x_pred = np.array(x_pred) # 描画用にnumpy配列変換 # 基準関数の表示用 x = np.arange(-10, 11, 1) y = f(x) # ここからグラフ描画------------------------------------------------- # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure() ax1 = fig.add_subplot(111) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('x') ax1.set_ylabel('y') # データプロットの準備。 ax1.plot(x, y, lw=1) ax1.scatter(x_pred, f(x_pred), color='red') # グラフを表示する。 fig.tight_layout() plt.show() plt.close() # ------------------------------------------------------------------- |
上記の説明とコード内のコメントを見比べて頂ければ、何となくやっていることがわかってくると思います。もし不明点がありましたらコメントを頂ければ回答致します。
実行結果
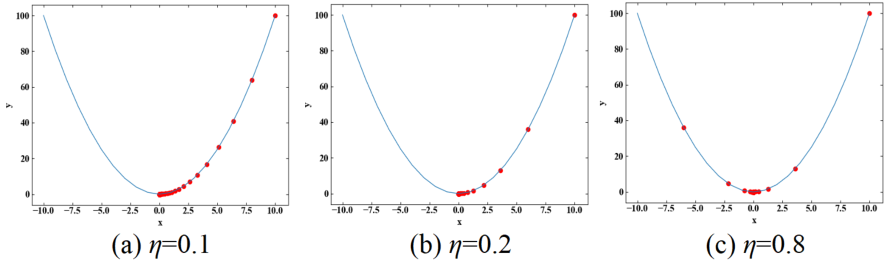
以下が実行結果です。赤い点は軌跡を表現しています。1000回のイテレーションは必要なかったかも知れません。
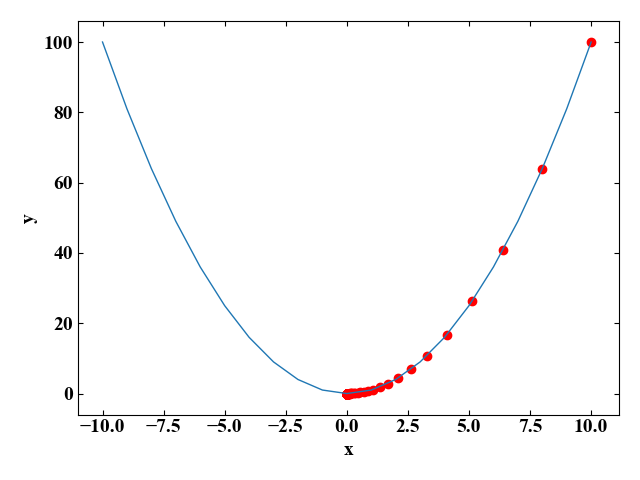
下図は学習率\(\eta\)違いで実行した結果です。\(\eta=0.8\)になると一度最小値を通り過ぎてから戻っていることがわかりました。
2変数関数の勾配降下法
全コード
続いて変数を1つ追加し、2変数関数の場合の勾配降下法コードを以下に示します。お試しする関数は式(8)です。変数が2つあるので、それぞれの変数で偏微分した結果が式(9)となります。
$$z=x^{2}+y^{2} (8)$$
$$\frac{\partial z}{\partial x}=2x, \frac{\partial z}{\partial y}=2y (9)$$
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 |
import numpy as np from matplotlib import pyplot as plt from mpl_toolkits.mplot3d import Axes3D # グラフプロット用基準関数 def f(x, y): z = x ** 2 + y ** 2 return z # 基準関数の微分 def df(x, y): dzdx = 2 * x dzdy = 2 * y dz = np.array([dzdx, dzdy]) return dz # 勾配降下法に必要なパラメータ eta = 0.1 # 学習率 max_iteration = 1000 # 最大反復回数 x0 = -10 # 初期値x0 y0 = 10 # 初期値y0 x_pred = [x0] # 描画用x0軌跡リスト(初期値をプリセット) y_pred = [y0] # 描画用y0軌跡リスト(初期値をプリセット) # 最大反復回数まで計算する for i in range(max_iteration): x0, y0 = np.array([x0, y0]) - eta * df(x0, y0) # 勾配降下法 x_pred.append(x0) # x0の軌跡をリストに追加 y_pred.append(y0) # y0の軌跡をリストに追加 print(i, x0, y0) x_pred = np.array(x_pred) # 描画用にx0をnumpy配列変換 y_pred = np.array(y_pred) # 描画用にx0をnumpy配列変換 z_pred = f(x_pred, y_pred) # 軌跡のz値を計算 # 基準関数の表示用 x = np.arange(-10, 11, 2) y = np.arange(-10, 11, 2) X, Y = np.meshgrid(x, y) Z = f(X, Y) # ここからグラフ描画---------------------------------------------------------------- # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # グラフの入れ物を用意する。 fig = plt.figure() ax1 = Axes3D(fig) # 軸のラベルを設定する。 ax1.set_xlabel('x') ax1.set_ylabel('y') ax1.set_zlabel('z') # データプロットする。 ax1.plot_wireframe(X, Y, Z, label='f(x, y)') ax1.scatter3D(x_pred, y_pred, z_pred, label='gd', color='red', s=50) # グラフを表示する。 plt.show() plt.close() # --------------------------------------------------------------------------------- |
実行結果
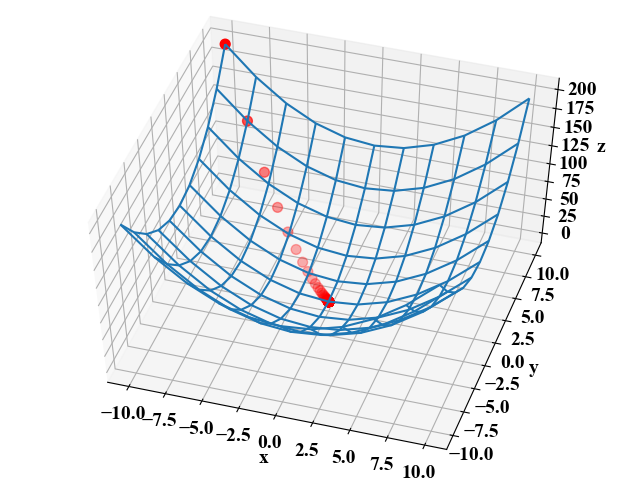
以下が実行結果です。初期値(\(x=-10, y=10\))から理論最小値(\(x=0, y=0\))に降下していく軌跡を見ることが出来ました。
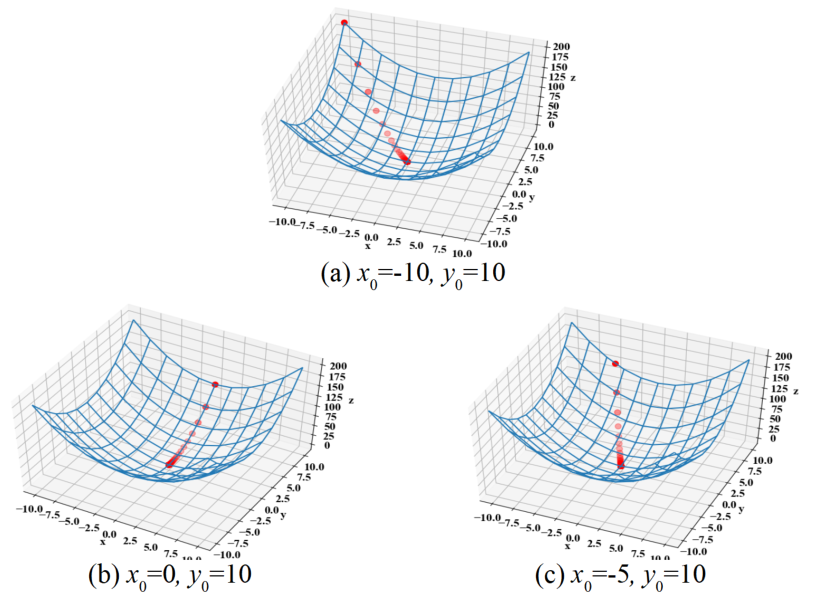
以下の図は初期値を変化させた時の動作結果です。どの場所に初期点を置いても、関数の勾配を使って降りてきていました。まずはこのコードで良さそうです(効率はさておき)。
今回はイテレーション数という反復計算数だけを計算終了条件に設定していましたが、勾配が無くなったら(閾値を設定する)計算を止めるという条件を設定した方が効率的だったかも知れません。
おまけ:2変数関数の勾配降下法②
全コード
せっかくなので、おまけとして降下中に方向を変えるような関数で試してみましょう。式(10)の関数であれば複数の山が出てくるので、斜めに初期点を配置すればそういった目的に対応できそうです。式(10)の偏微分は式(11)なので、これを実装してみます。
$$z=\sin x+\cos y (10)$$
$$\frac{\partial z}{\partial x}=\cos x, \frac{\partial z}{\partial y}=-\sin y (11)$$
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 |
import numpy as np from matplotlib import pyplot as plt from mpl_toolkits.mplot3d import Axes3D # グラフプロット用基準関数 def f(x, y): z = np.sin(x) + np.cos(y) return z # 基準関数の微分 def df(x, y): dzdx = np.cos(x) dzdy = - np.sin(y) dz = np.array([dzdx, dzdy]) return dz # 勾配降下法に必要なパラメータ eta = 0.4 # 学習率 max_iteration = 1000 # 最大反復回数 x0 = 2 # 初期値x0 y0 = -0.1 # 初期値y0 x_pred = [x0] # 描画用x0軌跡リスト(初期値をプリセット) y_pred = [y0] # 描画用y0軌跡リスト(初期値をプリセット) # 最大反復回数まで計算する for i in range(max_iteration): x0, y0 = np.array([x0, y0]) - eta * df(x0, y0) # 勾配降下法 x_pred.append(x0) # x0の軌跡をリストに追加 y_pred.append(y0) # y0の軌跡をリストに追加 print(i, x0, y0) x_pred = np.array(x_pred) # 描画用にx0をnumpy配列変換 y_pred = np.array(y_pred) # 描画用にx0をnumpy配列変換 z_pred = f(x_pred, y_pred) # 軌跡のz値を計算 # 基準関数の表示用 x = np.arange(0, 6, 0.2) y = np.arange(-5, 1, 0.2) X, Y = np.meshgrid(x, y) Z = f(X, Y) # ここからグラフ描画---------------------------------------------------------------- # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # グラフの入れ物を用意する。 fig = plt.figure() ax1 = Axes3D(fig) # 軸のラベルを設定する。 ax1.set_xlabel('x') ax1.set_ylabel('y') ax1.set_zlabel('z') # データプロットする。 ax1.plot_wireframe(X, Y, Z, label='f(x, y)') ax1.scatter3D(x_pred, y_pred, z_pred, label='gd', color='red', s=100) # グラフを表示する。 plt.show() plt.close() # --------------------------------------------------------------------------------- |
実行結果
以下が実行結果です。峰から降下する途中で最急方向を選んでいる様子が確認できました。
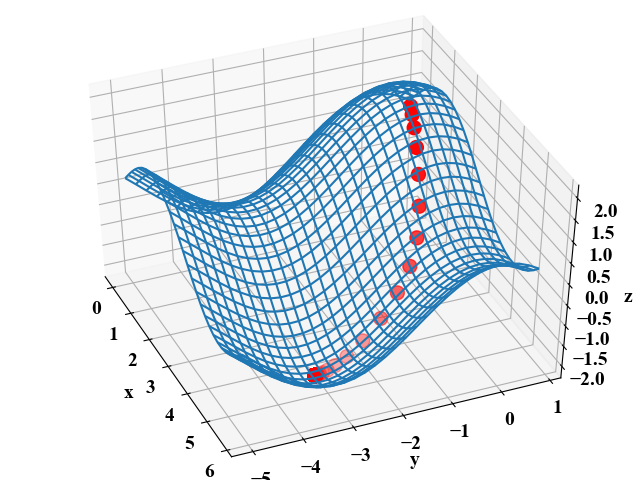
ゴルフみたい。
但し、このような最小値の沢山ある関数は初期値の選び方で勾配降下法の結果が変わります。
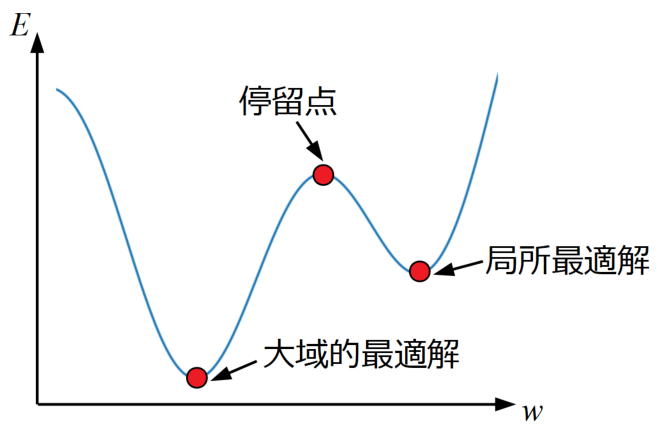
式(10)の関数であれば谷の最小値は全て同じ値ですが、最小値の深さが異なると勾配降下法で得られた解が局所最適解なのか大域的最適解なのかは不明になります。
以下の図のように、勾配が0になる点は複数あるので、この辺が最適化問題の難しい所になりそうですね(ある側面から見ると最小値でも、別の側面から見ると最大値をとる鞍点という点もあるようです)。
まとめ
本記事は勾配降下法(最急降下法)の概要を説明し、Pythonコードによる実装で1変数関数と2変数関数の場合の動作確認を行いました。
勾配降下法は関数の微分形を使って勾配を算出し、勾配の大小に学習率というゲインをかけて少しずつ最小値を探すというアルゴリズムであるということがわかりました。
多変数関数の場合は2変数関数の拡張で良さそうですが、今は偏微分を手動でやっている部分が手間です。
ディープラーニングでは自動微分として各ニューロンの勾配を算出し、チェーンルールを利用して最適化していくというアルゴリズムがあるそうなので、今後はその辺を学習していこうと思います。
勾配降下法は様々な最適化問題で活用できそうです!Twitterでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています!

 ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!
ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!

コメント