Pythonで窓関数が無い場合は？指数窓を自作してみる!

信号処理では良く窓関数を使うことがあります。PythonではNumPyやSciPyで窓関数を簡単に使うことができますが、今回指数窓が見つからなかったので窓関数自体を自作してみました。

窓関数を理解しよう!

窓関数とは？

窓関数とは、波形のある有限区間の範囲意外は0にする関数です。詳細はウィキペディアをご覧下さい。

Wiki：窓関数

信号処理で頻繁に使われるFFT（高速フーリエ変換）は変換する計測データが周期関数であることを仮定しています。

FFTはある有限のデータ長（フレーム）に対して計算を行いますが、実際に計測したデータはフレームの最初と最後が綺麗に繋がりません。そのようなデータを使ってFFTをかけてしまうと、計算によるノイズが周波数波形に乗ってしまうため、通常は窓関数を使って両端のデータが滑らかに0になるようにします。

窓関数のパッケージと自作の必要性

Pythonで信号処理をする場合、窓関数は通常自作する必要は無いと思っています。

SciPyという科学技術計算用パッケージを使えば、Wikiに載っているような窓関数は大抵あります。

それを使って楽に窓関数をかけようとしたのですが、今回のデータ（wav波形切り出し時のピアノ打鍵音）にかけたい窓関数が見つかりませんでした！
ちなみに、データはこちらの図。

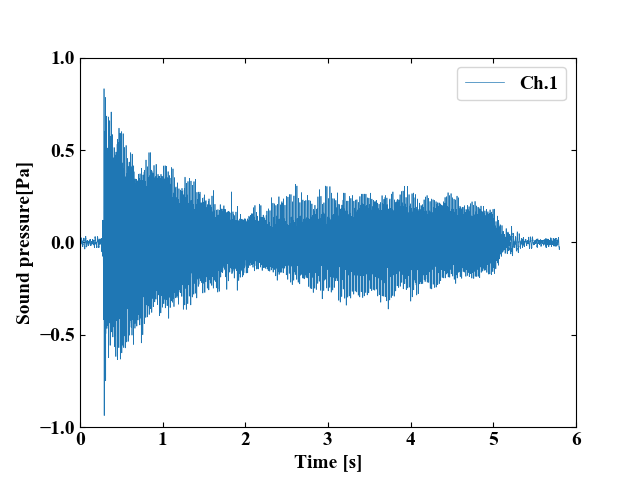
このような時間波形が左右非対称になっているデータは、衝撃に対する応答といった計測をすると得られます。機械工学の世界で扱う自由振動の波形と一緒ですね。

このようなデータをFFT分析する場合、一般的には指数窓をかけると思いますが、SciPyに見つけることができませんでした。そのため、今回は自作しようと思います！

※自作のため、内容に間違いがあるかもしれませんので、扱いにはご注意下さい。

指数窓の関数を作る

指数窓の式

窓関数を自作するにあたっては、式が必要になります。今回は以下の計測器メーカさんの公表している式を使ってみました。

National Instruments:Exponential Window

$$ y_{i}= x_{i}e^{\alpha i} \left ( i= 0,1,…,N-1 \right ) $$

$$ \alpha = \frac{logf}{N-1} $$

最初の式が指数窓をデータ\(x\)にかける部分で、その中で使っている\(\alpha\)は指数窓の減衰を決める係数です。\(f\)はデータフレームの最後の値にかける窓関数の係数最終値で、0でない小さい値を入れます（0だと0割のエラーが発生します）。\(N\)はフレームのデータ数です。

指数窓のコード

上の式を関数としてdef文でコードにすると以下になります。
データdataと係数の最終値\(f\)を引数に、\(N\)をデータ長から計算し、その後に\(\alpha\)を求めています。

\(x\)軸として1から1刻みで始まる配列を作り、最初に指数窓の縦軸係数coe(coefficientの意味）を作ります。最後に\(y\)としてデータに係数をかけ、戻り値として返します。
※ここではデータ確認のためにcoeも戻り値としています。

実行結果

以下の画像が実行結果です。元の波形（青）と窓関数適用後の波形（オレンジ）を比較しています。

\(f=0.3\)としているので、Exp. Windowの波形は最終値が0.3になっています。窓関数としては狙い通りですが、窓関数適用後はかなり元の波形と比べて形が変わっていますね。

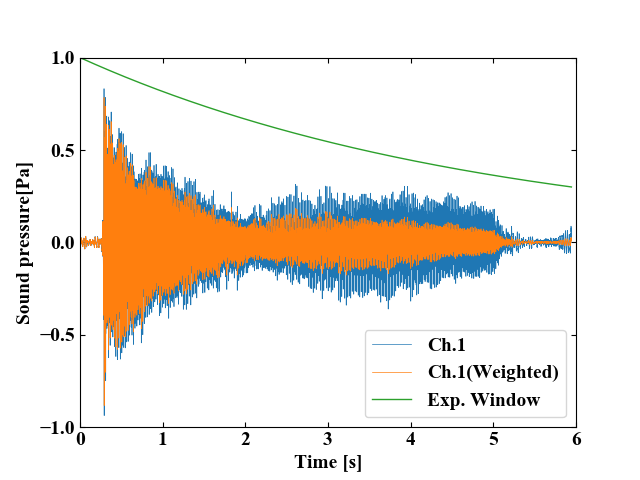
※データ分析の目的にもよりますが、この指数窓はデータの形を大きく変えてしまう可能性があるので注意が必要です（振動における減衰特性に影響を与えるため）。

極端に\(f=0.001\)とした場合はFFT波形は綺麗になるかも知れませんが、以下のように本来持っている時間波形の特徴（2s程度から波形の振幅が大きくなる）を消してしまっています。

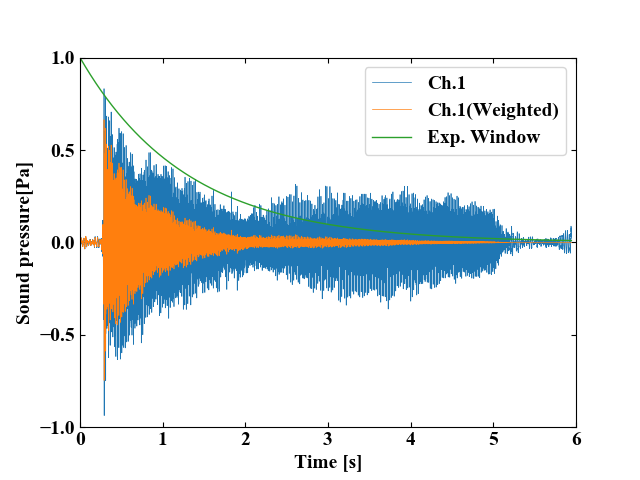
まとめ

PythonはSciPy等のパッケージで窓関数が多種用意されていますが、中には欲しい窓関数が無い場合もあります。

そんな時は自分で関数として作ってしまうことで、自由に窓関数を定義することができ、本記事ではその一連を説明しました。

しかし、窓関数は元のデータの形を大きく変化させてしまう可能性があるので、使用の際は分析の目的を再度確認し、生波形を見ながら適用することが重要です。