
Pythonで手を動かしながら基本情報技術者試験対策を行います。ここではコンピュータ内部の数値表現である2進数を始め、情報技術分野で重要となる8進数と16進数の概要を説明し、各基数変換を自由に計算できるようになる事を目標とします。
こんにちは。wat(@watlablog)です。ここではPythonでコードを書きながら2進数/8進数/16進数に慣れる事を目標とします!
基数とは?
基数(Radix)とは、漢字の通り基準の数という意味で、数値を表す際に各桁で重み付けの基本となっている数の事です。
言葉で説明すると難しそうですが、我々の生活で最も使われている10進数(Decimal number)が10を基数にしている事から考えると容易に理解する事が可能です。
例えば、10進数の1234は基数を使って考えると下図のように分解する事ができます。このように数値を各桁で分解し、基数の0乗、1乗…と桁毎に重みを乗算、最後に足し合わせる事で数が成り立っています。
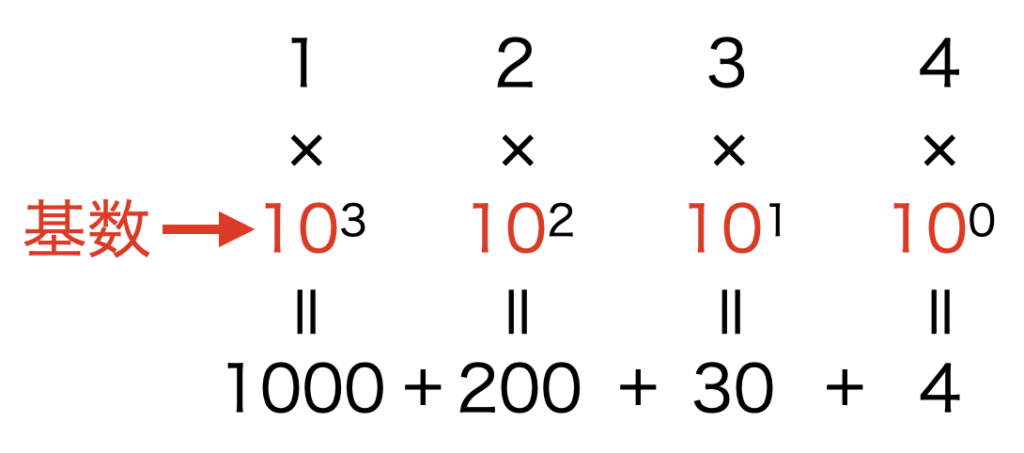
このルールを使って、2を基数にした数を2進数(Binary number)、8を基数にした数を8進数(Octal number)、16を基数にした数を16進数(Hexadecimal number)とそれぞれ呼びます。
2進数の概要と基数変換
コンピュータは2進数が基本
人間は手の指が左右合計10本あった事でたまたま10進数を使っているようですが、コンピュータは2進数を基本としています。
10進数の0→1→2→3という数は、2進数では0→1→10→11となり、0と1のたった二つだけの数を使います。
これはコンピュータが10進数を扱う事が困難で、電圧がかかっている(1)かかかっていない(0)かで数を表現する事に由来しています。
複数の基数が混在している場合、括弧に基数を字下げで書く記法がよく使われます。例えば「\(1111\)」だけだと10進数なのか2進数なのかわかりませんが、「\((1111)_{2}\)」と書く事で2進数と明示する事が可能です。
しかしながら、\((01)_{2}\)のような下付き文字はプレーンテキストでは扱えない事から、コンピュータ分野では2進数の場合は先頭に「0b」や「0B」という文字(プレフィックス)を付ける事が一般的のようです(場合によって使い分けた方が良さそうですね)。
2進数から10進数への基数変換(Pythonコード付き)
基数変換(Radix conversion)とは、ある基数を持つ数を異なる基数を持つ数に変換する事です。ここでは2進数から10進数への変換を例に説明します。
基数のルールを使って2進数「\((1111)_{2}\)」を分解した下図そのものが10進数への基数変換方法の説明図となります。
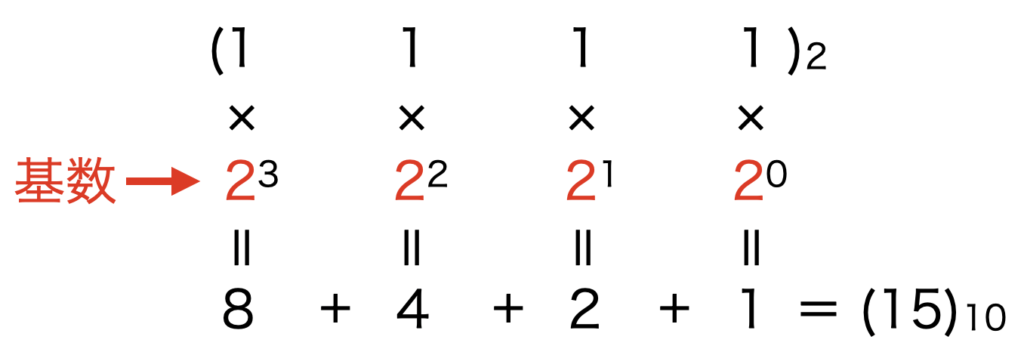
Pythonで書くと以下のアルゴリズムになります。桁数を計算したり一桁ずつ抽出するために文字列変換を活用しています。
基本情報技術者試験対策として、アルゴリズムの理解のためにあえて関数化していますが、Pythonの組み込み関数であるint()の第二引数に基数を指定する事でも10進数に変換する事が可能です。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
# 2進数を10進数に変換する関数 def binary2decimal(binary): binary = str(binary) n = len(binary) digits = [] for i in range(n): digits.append(int(binary[i]) * 2 ** (n-1 - i)) decimal = sum(digits) return decimal # 2進数の定義と関数の実行 binary = 1111011 decimal = binary2decimal(binary) print('0b', binary, '=', decimal) # Pythonの組み込み関数で変換する場合(intの第二引数で基数を指定) print(int(str(binary), 2)) |
結果はこちら。自作関数と組み込み関数で結果が一致する事を確認しました。
|
1 2 |
0b1111011=123 123 |
10進数から2進数への基数変換(Pythonコード付き)
10進数から2進数への基数変換は、10進数をひたすら2で割っていき、余りを求める事で計算する事ができます。
下図は\((123)_{10}\)を2で割っていき、割る数が0になるまで除算、余りを下から並べていく事で2進数に変換した例です。先ほどの「2進数から10進数への変換」を例に検算すると、123に戻る事が確認できるでしょう。
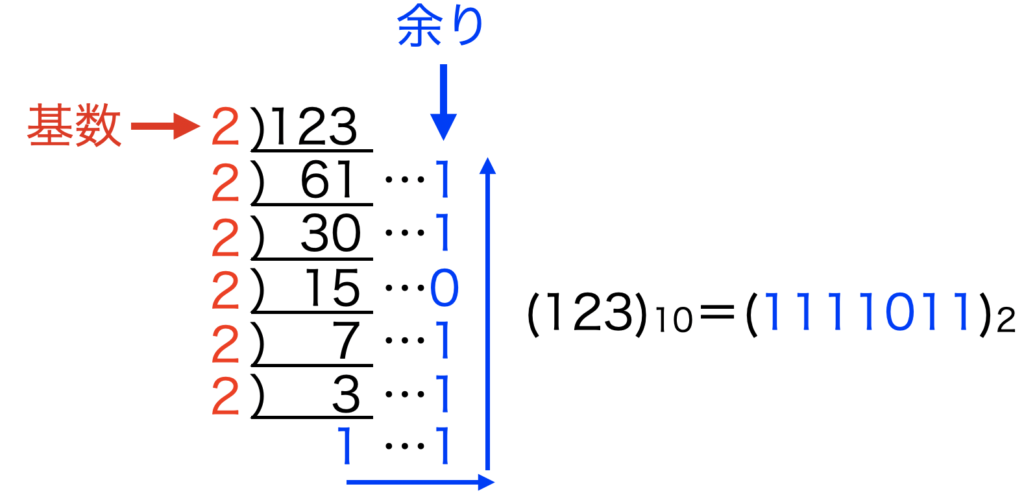
Pythonコードで書くと以下となります。ここでは割られた数(10進数)が0になるまでwhileループで商の整数部を求める処理と商の余りを求める処理を続けるアルゴリズムを採用しています。おまけでPythonの組み込み関数で2進数に変換するbin()も載せています。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
# 10進数整数を2進数に基数変換する関数 def decimal2binary(decimal): binary = [] while decimal != 0: binary.insert(0, decimal % 2) decimal = decimal // 2 # リスト内数値を繋げて一つの数値にする binary = int("".join(map(str, binary))) return binary # 10進数整数の定義と関数の実行 decimal = 123 binary = decimal2binary(decimal) print(decimal, '=', '0b', binary) # Pythonの組み込み関数で変換する場合 print(bin(decimal)) |
ちなみに、while文の1行目(decimal % 2)と2行目(decimal // 2)を逆に書くと先にdecimalの値が書き変わってしまって計算ミスとなります。基本情報技術者試験令和1年秋の問1はこのような順番を理解していないと解けないようになっていたようです。
以下が結果です。bin()では2進数である事を明示する「0b」というプレフィックスが元々頭に付いていますが、自作した関数と基数変換値が一致した事を確認しました。
|
1 2 |
123=0b1111011 0b1111011 |
小数点を扱いたい時は、小数点以下を一つの整数として考えるような処理を加える必要がありますが、今回はその部分まで考慮していません。整数の場合は2で割っていくという操作をしましたが、小数の場合は小数部が0になるまで2倍していく方法をとります(考え方は同じ)。
8進数と16進数の概要と基数変換
8進数と16進数は便利さから活用される
コンピュータは2進数を基礎としていますが、なぜ8進数や16進数も必要になるのでしょうか?
ちなみにプレフィックスは8進数がOctalに由来して「0o」、16進数がHexadecimalに由来して「0x」です。
正直、非ITエンジニアの自分にはあまりしっくり来なかったので、ちょっと参考書を見たりググったりしてみました。
僕が購入した以下の基本情報技術者試験の対策本には「本来は2進数で扱いたいが、桁数が多く間違いやすいから8進数や16進数が使われる」とありました。
また、8進数については、外部記事で以下の記述も見られます。2進数を8進数に基数変換する時は3ビットずつに区切るので、コンピュータの歴史にも由来していそうです。
実は、その昔、コンピュータの処理ビット数は3の倍数が普通でした。たとえば、IBMの70xシリーズや70xxシリーズは36bit機(例:701, 7094) 、DECのPDP-7は18bit機、PDP-8は12bit機(参考)、UNIVAC 1000は24bit機(参考)など。
知ってた?8進数のナゾ
やはり本来は2進数で全て扱いたい所だけど、人間とのインターフェースとして16進数等が出てきたというだけのようです(コンピュータの進化から8進数は今はほとんどないかも)。
たしかに、「何歳なんですか?」と聞いた時に、
0b10100歳になりました。
といわれるより、
0x14歳になりました。
といわれた方が桁数が少ないのでわかりやすいですね。人類なら10進数で話してほしいですが、Twitterを見てるとたまに16進数で会話している人が実際にいてびびります。
ビット
先ほどビット(bit)という単語が出てきましたが、2進数を基本として8進数と16進数を扱う上ではこれらの概念を知る事が便利ですので触れておきます。
binary digitが由来なビットは、2進数の一桁の事を意味します。コンピュータでは数値を格納する入れ物のサイズが決まっていて、通常コンピュータで2進数を扱う時は入れ物のサイズに合わせて数を表現します。
例えば、8ビットの入れ物で\((111)_{2}\)を表す時は、以下のように数値を右詰にして、全体で8ビットになるように左側を0で埋めます。
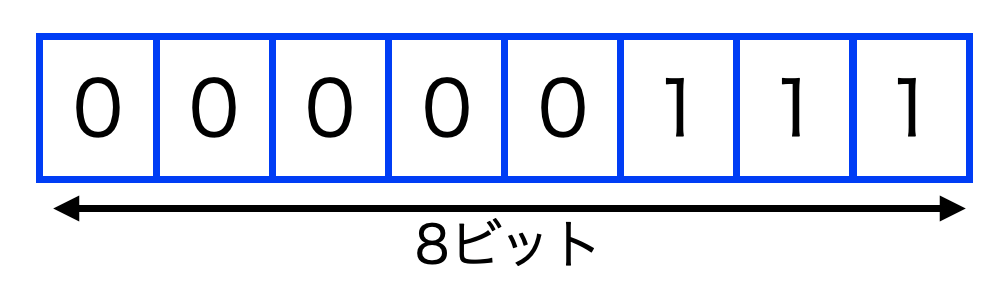
指定したサイズの左側を0で埋めるPythonコードは.formatが便利です。
|
1 2 |
a = str('{:08}'.format(111)) print(a) |
{:0桁数}とフォーマットを指定すると以下の結果を得ます。
|
1 |
00000111 |
2進数から8進数への基数変換(Pythonコード付き)
2進数から8進数への基数変換を考えてみましょう。例題として\((1010)_{2}\)を変換します。
8進数への変換は、2進数を3ビットずつに分けて基数変換します。ここで、\((1010)_{2}\)は数値としては4ビット分の情報しかありませんが、3で割り切れるビット数になるように左側を0で埋めると\((001010)_{2}\)となります。
2進数を変換するので、基数は2です。3ビット毎に分割した後は2を基数とした基数変換を行って数値を並べる事で8進数の数となります。
図解すると以下。図にすると簡単に理解する事ができますね。
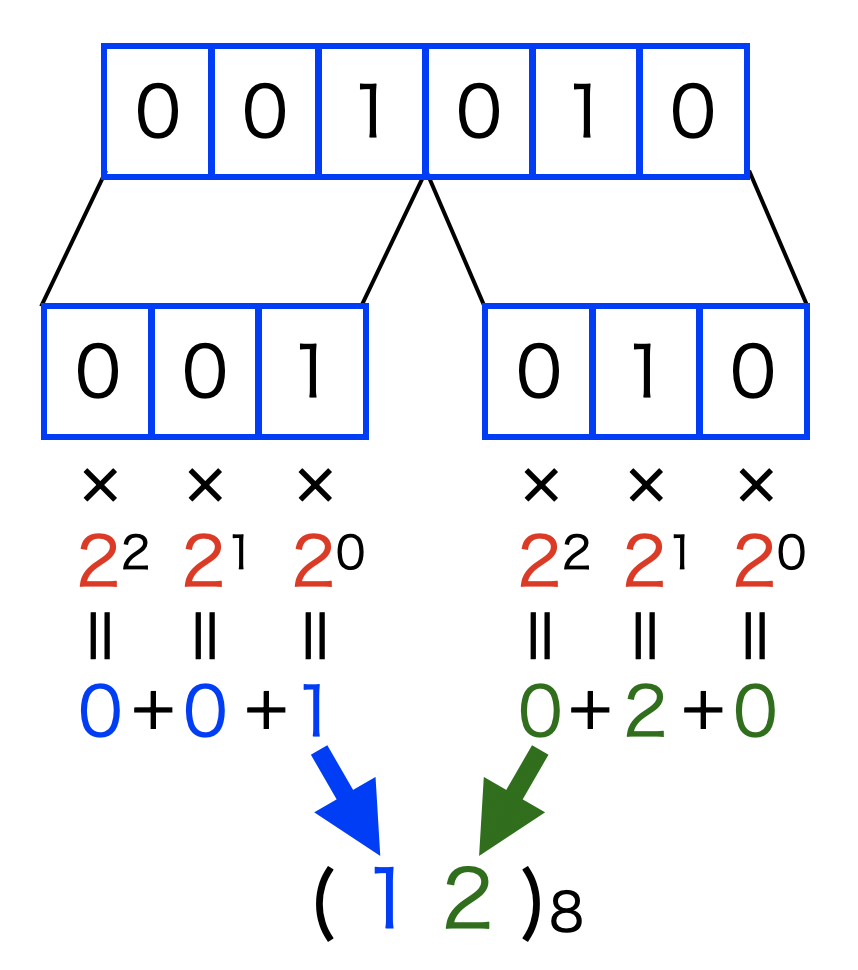
参考までに、Pythonコードを作ってみました。問題集等では予めビット数を固定にした場合のフローチャートが多いようですが、ここではどんな桁数の2進数が来ても3ビットで割り切れるビット数に調整してから8進数変換するようにしてみました(こういうプログラムを考えるのは頭の体操にちょうど良いかも)。
例に則りPython組み込み関数であるoct()による基数変換例も載せています。この辺から1行で完結する組み込み関数のありがたさがわかりますね…。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 |
# 2進数を8進数に基数変換する関数 def binary2octal(binary): # どんな桁数の2進数が来ても、3ビットの倍数サイズにフォーマットする n = len(str(binary)) n_bit = n bit = 3 while n_bit % bit != 0: n_bit += 1 binary = str(('{:0' + str(n_bit) + '}').format(binary)) # 3ビットずつ抽出 octal = [] for i in range(n_bit // bit): extract = binary[i * bit:(i * bit) + bit] # 2進数の桁の重みをかけて加算 digits = [] for j in range(bit): digits.append(int(extract[j]) * 2 ** (bit - 1 - j)) octal.append(sum(digits)) # 8進数としてまとめる octal = int("".join(map(str, octal))) return octal # 2進数の定義と関数の実行 binary = 1010 octal = binary2octal(binary) print('0o', octal) # Pythonの組み込み関数で変換する場合 print(oct(int(str(binary), 2))) |
以下が結果。組み込み関数計算値と一致しました。
|
1 2 |
0o 12 0o12 |
2進数から16進数への基数変換(Pythonコード付き)
2進数から16進数の変換は、4ビットずつ分割するという部分に気をつければ8進数の時と同様の変換方法となります。
そして「10=a」, 「11=b」,「12=c」,「13=d」,「14=e」,「15=f」と10以降を一文字で表す事にも注意が必要です。
これも以下の図解を見れば一目瞭然と思います。
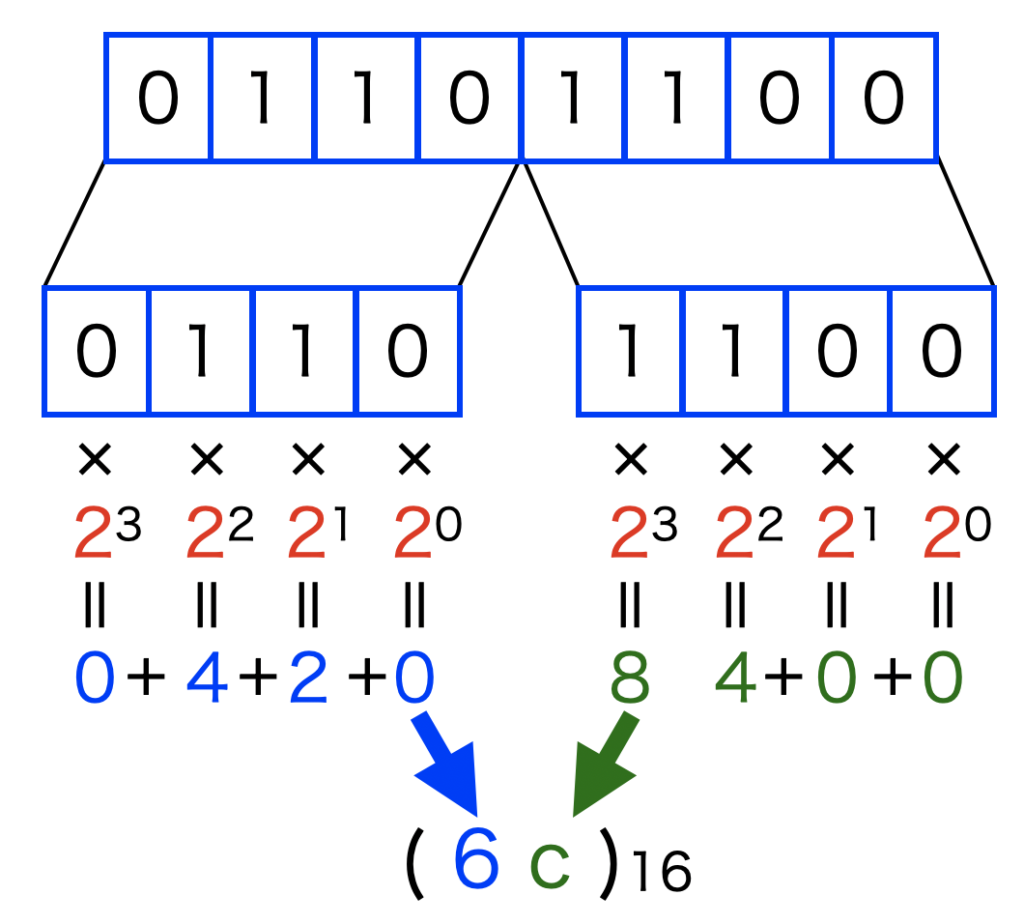
Pythonコードですが、実は先ほどの8進数変換の関数は16進数変換への拡張を考えて書いていたので、bit値を4に変更する事と、文字列変換部分の追加のみで16進数の基数変換コードが実現可能です。
Python組み込み関数による答え合わせはhex()で行っています。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 |
# 2進数を16進数に基数変換する関数 def binary2hexadecimal(binary): # どんな桁数の2進数が来ても、4ビットの倍数サイズにフォーマットする n = len(str(binary)) n_bit = n bit = 4 while n_bit % bit != 0: n_bit += 1 binary = str(('{:0' + str(n_bit) + '}').format(binary)) # 4ビットずつ抽出 hexadecimal = [] for i in range(n_bit // bit): extract = binary[i * bit:(i * bit) + bit] # 2進数の桁の重みをかけて加算 digits = [] for j in range(bit): digits.append(int(extract[j]) * 2 ** (bit - 1 - j)) # 16進数の文字列部分を照合 hex_num = sum(digits) if hex_num < 10: string = str(hex_num) else: string = 'abcdef'[hex_num - 10] hexadecimal.append(string) # 16進数としてまとめる hexadecimal = "".join(map(str, hexadecimal)) return hexadecimal # 2進数の定義と関数の実行 binary = 1101100 hexadecimal = binary2hexadecimal(binary) print('0x', hexadecimal) # Pythonの組み込み関数で変換する場合 print(hex(int(str(binary), 2))) |
以下が結果。問題ないですね。
|
1 2 |
0x 6c 0x6c |
8進数から2進数への基数変換(Pythonコード付き)
2進数から8進数への逆算(上図の矢印を逆に考える)を行う事で、8進数から2進数の変換が可能です。
Pythonコードはこちら。指定した8進数であるoctalを1文字ずつ2進数へ基数変換し、3ビットの入れ物に入れて結合するというアルゴリズムを書いてみました。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
# 8進数を2進数に基数変換する関数 def octal2binary(octal): bit = 3 n = len(str(octal)) binary_list = [] for i in range(n): extract = int(str(octal)[i]) binary = [] # 抽出した数を2進数へ基数変換 while extract != 0: binary.insert(0, extract % 2) extract = extract // 2 binary_list.append(('{:0' + str(bit) + '}').format(int("".join(map(str, binary))))) binary_final = int("".join(map(str, binary_list))) return binary_final # 8進数の定義と関数の実行 octal = 12 binary = octal2binary(octal) print('0b', binary) # Pythonの組み込み関数で変換する場合 print(bin(int(str(octal), 8))) |
結果はこちら。Python組み込み関数との答え合わせも問題ありません。ここではあえてintで出力する方式にしていますが、3ビットの倍数サイズである文字列そのまま返す方式でも良いかも。ただ今回はアルゴリズム学習で自作関数作りましたが、実務では組み込み関数を使うと思うのでどっちでも良いか。
|
1 2 |
0b 1010 0b1010 |
16進数から2進数への基数変換(Pythonコード付き)
8進数と同様の方法に、文字列変換を加えるだけで16進数を2進数に変換するコードができます。抽出した16進数が文字列かどうか判定するのにin演算子を使い、文字列の位置検索に.find()を使っている所くらいが特徴です。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
# 16進数を2進数に基数変換する関数 def hexadecimal2binary(hexadecimal): bit = 4 chord = 'abcdef' n = len(str(hexadecimal)) binary_list = [] for i in range(n): # 16進数の文字列部分を照合 if str(hexadecimal)[i] in chord: extract = 10 + chord.find(str(hexadecimal)[i]) else: extract = int(str(hexadecimal)[i]) # 抽出した数を2進数へ基数変換 binary = [] while extract != 0: binary.insert(0, extract % 2) extract = extract // 2 binary_list.append(('{:0' + str(bit) + '}').format(int("".join(map(str, binary))))) binary_final = int("".join(map(str, binary_list))) return binary_final # 16進数の定義と関数の実行 hexadecimal = '6c' binary = hexadecimal2binary(hexadecimal) print('0b', binary) # Pythonの組み込み関数で変換する場合 print(bin(int(str(hexadecimal), 16))) |
結果はこちら。組み込み関数の変換値と一致しました。
|
1 2 |
0b 1101100 0b1101100 |
まとめ
この記事ではコンピュータの基礎である2進数、8進数、16進数と基数の考え方を整理し、各基数変換の方法を紹介しました。
都度Pythonによるフルスクラッチを考える事で、基数変換の方法を理解する事ができました。
Pythonは良いか悪いかわかりませんが、プログラミングに関するハードルがかなり低い言語です。そのため考えたアルゴリズムを試す、とりあえず動かす、というアルゴリズムの学習にはコスパ抜群なのではないかと思います(但し、業務活用にはその他言語と同様に型とかメモリとか考慮する必要があると思います)。
今回は基本情報技術者試験の参考書を読みながら、理解を得るためにフルスクラッチをしてみましたが、今後もアルゴリズム系はブログでアウトプットしつつ理解を深めたいと思います(用語系とかはまとめないと思います)。
基数変換完全に理解した!(「チュートリアル終わった」の意)
Twitterでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています!

 ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!
ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!
