
iOSデバイスで高速フーリエ変換を実装する方法を紹介します。この記事では、まずはじめに一般的な高速フーリエ変換(FFT)であるCooley-Tukey法をSwiftで検証し、その後Accelerateというライブラリによる実装方法も併せて紹介します。
こんにちは。wat(@watlablog)です。この記事ではSwiftによる高速フーリエ変換について色々まとめてみます!
この記事の目標
Cooley-Tukey法によるFFTコードを自分で書いてみる
ここしばらく筆者はiPhoneアプリ制作をしてみたいと思い、基礎文法のチェックや録音の仕方、音声再生方法や画面遷移の方法を個別の記事で取り上げました。信号処理アプリを作る目標を立てており、この分野ではかかせない周波数分析機能に着手するのがこの記事の内容です。
WATLABブログでは以下の記事で前回離散フーリエ変換(DFT)をPythonやSwiftで実装してみました。
・Pythonで検証しながらSwiftで離散フーリエ変換を実装する
そして次に高速フーリエ変換(FFT)のアルゴリズムをPythonで学びました。
・Pythonで高速フーリエ変換をCooley-Tukey法で書く
慣れもあるかもしれませんが、Pythonはこのようなコードを書くのが本当に楽です。先ほどの記事で基本的なFFT関数の作り方を学んだので、この記事ではまず同様にCooley-Tukey法をSwiftに移植してみます。
AccelerateでFFTを使ってみる
ただ、Pythonで実感したのは自分で実装したFFT関数よりもNumPy等の外部ライブラリを使った方が圧倒的に高速だということでした。基本的なアルゴリズムを学ぶために自分でコードを書いてみるのは非常に良いことですが、実用には既存のライブラリを使った方が良いと思います。
そのためこの記事では一度Cooley-Tukey法を書いてみた後に、SwiftのAccelerateというライブラリを使ってFFTを使う方法も学びます。
動作環境
この記事のコードは以下の開発環境で動作を確認しました。
| Mac | OS | macOS Ventura 13.2.1 |
|---|---|---|
| CPU | 1.4[GHz] | |
| メモリ | 8[GB] | |
| Xcode | Version | 14.3(14E222b) |
| Swift | Version | 5.8(swiftlang-5.8.0.124.2 clang-1403.0.22.11.100) |
| iPhone SE2 | OS | iOS 16.3.1 |
SwiftでCooley-Tukey法によるFFTをフルスクラッチするコード
事前準備
まずは自作のFFTコードから書いてみますが、動作検証のためにいくつか事前準備を行います。
データ点数を指定して配列を作成する関数
FFTのアルゴリズムを効果的に使用するためにはデータ点数が2の冪乗でないとなりません。Swiftでメソッドがあるかどうか探せなかったので、まずはデータ点数を自由に指定するために以下のlinspace関数を作りました。Pythonのnp.linspace()を真似たのですが、これでFFTコードの検証がしやすくなります。
|
1 2 3 4 5 6 |
func linspace(start: Float, stop: Float, num: Int) -> [Float] { // データ点数を指定して配列を作成する関数 let increment = (stop - start) / Float(num - 1) return (0..<num).map { Float($0) * increment + start } } |
サンプル波形を生成する関数
上記データ点数を指定するlinspace関数を使って、サイン波を作るwavePoints関数も用意しておきます。サイン波は周波数や時間長を変更できます。また、コードの検証としては直流成分も確認したいため、dcで0[Hz]の時の振幅を定義できるようにしています。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
func wavePoints(N: Int, length: Float) -> (xArray: [Float], yArray: [Float]){ // プロットするデータを演算する関数 // データ点数Nと時間長lengthからx軸を作成 let xArray = linspace(start: 0.0, stop: length, num: N) // 正弦波を作成。A:振幅、f:周波数[Hz]、dc:直流成分 let A: Float = 1 let f: Float = 100 let dc: Float = 1 let yArray = xArray.map{ A * sin(2 * .pi * f * $0) + dc } return (xArray, yArray) } |
複素数構造体を定義
Swiftには標準で複素数型がありません。そのためstructを使ってComplex構造体を定義します。詳細は離散フーリエ変換の記事で書いた通りです。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
struct Complex { // 複素数型の構造体を定義 // re:実部、im:虚部 var re: Float var im: Float // Complex + Complexの場合の演算処理 static func +(lhs: Complex, rhs: Complex) -> Complex { return Complex(re: lhs.re + rhs.re, im: lhs.im + rhs.im) } // Complex * Complexの場合の演算処理 static func *(lhs: Complex, rhs: Complex) -> Complex { return Complex(re: lhs.re * rhs.re - lhs.im * rhs.im, im: lhs.re * rhs.im + lhs.im * rhs.re) } // Complex * Floatの場合の演算処理 static func *(lhs: Complex, rhs: Float) -> Complex { return Complex(re: lhs.re * rhs, im: lhs.im * rhs) } } |
FFT関数(Cooley-Tukey法)
こちらがSwiftで書いたCooley-Tukey法によるFFT関数です。先ほど紹介したPythonによるFFTの記事と同じ書き方をしているので、Pythonユーザーは是非両コードを見比べてみてください。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 |
func fft(_ x: [Float]) -> [Complex] { // FFT Cooley-Tukey法 // 標本点数 let N = x.count // Nが1なら、そのままxを返す if N == 1 { return [Complex(re: x[0], im: 0)] } // ビット反転順序に基づいて、偶数インデックスと奇数インデックスの部分配列を得る var evenArray: [Float] = [] var oddArray: [Float] = [] for i in 0..<N { if i % 2 == 0 { evenArray.append(x[i]) } else { oddArray.append(x[i]) } } let even = fft(evenArray) let odd = fft(oddArray) // DFTの結果を格納するための複素数配列 var T: [Complex] = [] for k in 0..<N { let theta = -2.0 * Float.pi * Float(k) / Float(N) T.append(Complex(re: cos(theta), im: sin(theta))) } // 偶数部分と奇数部分のDFTを組み合わせる(バタフライ演算) var F: [Complex] = [] for k in 0..<N { if k < N / 2 { F.append(even[k] + T[k] * odd[k]) } else { F.append(even[k - N / 2] + T[k] * odd[k - N / 2]) } } return F } |
全コード(コピペ動作OK)
UI部分を含めた全コードを以下に示します。freqLimitはなくても動作しますが、グラフに表示させる周波数を絞ることを目的としています。グラフへの表示は以下の記事で紹介したChartを使っています。
・SwiftUI:iOS16から追加されたChartsでグラフを作成
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 |
import SwiftUI import Charts struct PointsData: Identifiable { // 点群データの構造体 var xValue: Float var yValue: Float var id = UUID() } struct ContentView: View { // データを定義 @State private var data: [PointsData] = [] @State private var x: [Float] = [] @State private var y: [Float] = [] func linspace(start: Float, stop: Float, num: Int) -> [Float] { // データ点数を指定して配列を作成する関数 let increment = (stop - start) / Float(num - 1) return (0..<num).map { Float($0) * increment + start } } func wavePoints(N: Int, length: Float) -> (xArray: [Float], yArray: [Float]){ // プロットするデータを演算する関数 // データ点数Nと時間長lengthからx軸を作成 let xArray = linspace(start: 0.0, stop: length, num: N) // 正弦波を作成。A:振幅、f:周波数[Hz]、dc:直流成分 let A: Float = 1 let f: Float = 100 let dc: Float = 1 let yArray = xArray.map{ A * sin(2 * .pi * f * $0) + dc } return (xArray, yArray) } struct Complex { // 複素数型の構造体を定義 // re:実部、im:虚部 var re: Float var im: Float // Complex + Complexの場合の演算処理 static func +(lhs: Complex, rhs: Complex) -> Complex { return Complex(re: lhs.re + rhs.re, im: lhs.im + rhs.im) } // Complex * Complexの場合の演算処理 static func *(lhs: Complex, rhs: Complex) -> Complex { return Complex(re: lhs.re * rhs.re - lhs.im * rhs.im, im: lhs.re * rhs.im + lhs.im * rhs.re) } // Complex * Floatの場合の演算処理 static func *(lhs: Complex, rhs: Float) -> Complex { return Complex(re: lhs.re * rhs, im: lhs.im * rhs) } } func fft(_ x: [Float]) -> [Complex] { // FFT Cooley-Tukey法 // 標本点数 let N = x.count // Nが1なら、そのままxを返す if N == 1 { return [Complex(re: x[0], im: 0)] } // ビット反転順序に基づいて、偶数インデックスと奇数インデックスの部分配列を得る var evenArray: [Float] = [] var oddArray: [Float] = [] for i in 0..<N { if i % 2 == 0 { evenArray.append(x[i]) } else { oddArray.append(x[i]) } } let even = fft(evenArray) let odd = fft(oddArray) // DFTの結果を格納するための複素数配列 var T: [Complex] = [] for k in 0..<N { let theta = -2.0 * Float.pi * Float(k) / Float(N) T.append(Complex(re: cos(theta), im: sin(theta))) } // 偶数部分と奇数部分のDFTを組み合わせる(バタフライ演算) var F: [Complex] = [] for k in 0..<N { if k < N / 2 { F.append(even[k] + T[k] * odd[k]) } else { F.append(even[k - N / 2] + T[k] * odd[k - N / 2]) } } return F } var body: some View { // UI VStack{ Chart { // データ構造からx, y値を取得してプロット ForEach(data) { shape in LineMark( x: .value("x", shape.xValue), y: .value("y", shape.yValue) ) } } .padding(.all, 10) Button("Button"){ // ボタンイベント // 関数を実行してx, y演算結果を取得 let result = wavePoints(N: 8192, length: 10) let x = result.xArray let y = result.yArray // FFTを計算 let fftResult = fft(y) // FFTの結果から振幅を計算 var amp: [Float] = [] for i in 0..<fftResult.count { let re = fftResult[i].re let im = fftResult[i].im let magnitude = sqrt(re * re + im * im) if i == 0 { // 直流成分 amp.append(magnitude / Float(fftResult.count)) } else { // 変動成分 amp.append(2 * magnitude / Float(fftResult.count)) } } // 周波数軸を計算 let dt = x[1] - x[0] // 時間刻み var freq: [Float] = [] for k in 0..<x.count { freq.append(Float(k) / (Float(x.count) * dt)) } // 周波数の上限を指定 let freqLimit: Float = 300.0 let limitIndex = Int(freqLimit * Float(fftResult.count) * dt) let filteredFreq = freq[..<limitIndex] let filteredAmp = amp[..<limitIndex] // プロットデータの全削除 data.removeAll() // プロットデータの追加 for i in 0..<filteredFreq.count { data.append(.init(xValue: filteredFreq[i], yValue: filteredAmp[i])) } } } } } struct ContentView_Previews: PreviewProvider { static var previews: some View { // プレビュー ContentView() } } |
実行結果
下図が実行結果の例です。Buttonをタップすると波形が表示されます。これはwavePointsで生成された時間波形をfft関数で高速フーリエ変換した結果です。指定した通りのピークがでました。
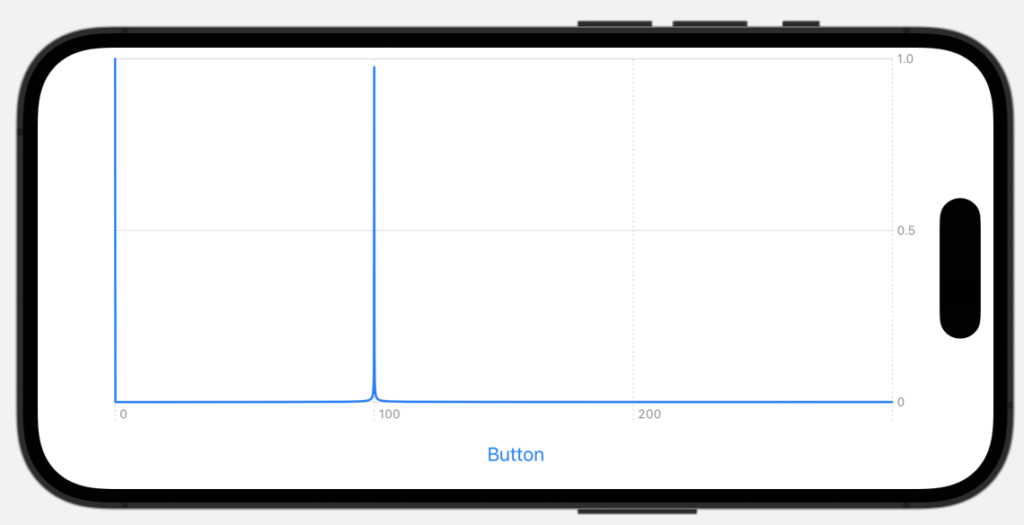
freqLimitを外したコード、もしくはfreqLimitの上限を最大まで持っていった場合は下図になります。fft関数で計算された値は鏡像ピークまで入っている結果です。
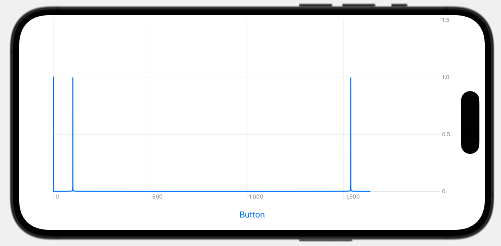
SwiftのAccelerate/vDSPでFFTをするコード
全コード
それではAccelerateというライブラリのvDSPを使ってみます。上記のコードをvDSPを使って書いたコードを以下に示します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 |
import SwiftUI import Charts import Accelerate struct PointsData: Identifiable { // 点群データの構造体 var xValue: Float var yValue: Float var id = UUID() } struct ContentView: View { // データを定義 @State private var data: [PointsData] = [] @State private var x: [Float] = [] @State private var y: [Float] = [] @State private var showingAlert = false func linspace(start: Float, stop: Float, num: Int) -> [Float] { // データ点数を指定して配列を作成する関数 let increment = (stop - start) / Float(num - 1) return (0..<num).map { Float($0) * increment + start } } func wavePoints(N: Int, length: Float) -> (xArray: [Float], yArray: [Float]){ // プロットするデータを演算する関数 // データ点数Nと時間長lengthからx軸を作成 let xArray = linspace(start: 0.0, stop: length, num: N) // 正弦波を作成。A:振幅、f:周波数[Hz]、dc:直流成分 let A: Float = 1 let f: Float = 100 let dc: Float = 1 let yArray = xArray.map{ A * sin(2 * .pi * f * $0) + dc } return (xArray, yArray) } struct Complex { // 複素数型の構造体を定義 // re:実部、im:虚部 var re: Float var im: Float // Complex + Complexの場合の演算処理 static func +(lhs: Complex, rhs: Complex) -> Complex { return Complex(re: lhs.re + rhs.re, im: lhs.im + rhs.im) } // Complex * Complexの場合の演算処理 static func *(lhs: Complex, rhs: Complex) -> Complex { return Complex(re: lhs.re * rhs.re - lhs.im * rhs.im, im: lhs.re * rhs.im + lhs.im * rhs.re) } // Complex * Floatの場合の演算処理 static func *(lhs: Complex, rhs: Float) -> Complex { return Complex(re: lhs.re * rhs, im: lhs.im * rhs) } } func isPowerOfTwo(_ n: Int) -> Bool { // 入力が2のべき乗であるかどうかを判断する関数 return (n != 0) && ((n & (n - 1)) == 0) } func fft(_ x: [Float]) -> [Complex] { // 入力データの長さが2のべき乗であることを確認 let log2n = vDSP_Length(log2(Double(x.count)).rounded(.up)) let n = 1 << log2n // 入力データを複素数形式に変換 var real = x var imaginary = [Float](repeating: 0.0, count: n) var splitComplexInput = DSPSplitComplex(realp: &real, imagp: &imaginary) // FFTの設定を行います。 let fftSetup = vDSP_create_fftsetup(log2n, FFTRadix(kFFTRadix2))! // FFTを適用します。 vDSP_fft_zip(fftSetup, &splitComplexInput, 1, log2n, FFTDirection(kFFTDirection_Forward)) // 複素数の出力結果を作成します。 var output = [Complex]() for i in 0..<n { output.append(Complex(re: splitComplexInput.realp[i], im: splitComplexInput.imagp[i])) } // FFT設定を解放します。 vDSP_destroy_fftsetup(fftSetup) return output } var body: some View { // UI VStack{ Chart { // データ構造からx, y値を取得してプロット ForEach(data) { shape in LineMark( x: .value("x", shape.xValue), y: .value("y", shape.yValue) ) } } .padding(.all, 10) Button("Button"){ // ボタンイベント // 関数を実行してx, y演算結果を取得 let result = wavePoints(N: 8192, length: 10) let x = result.xArray let y = result.yArray // データ点数が2のべき乗であることを確認 guard isPowerOfTwo(x.count) else { // データ点数が2のべき乗でない場合、アラートを表示 showingAlert = true return } // FFTを計算 let fftResult = fft(y) // FFTの結果から振幅を計算 var amp: [Float] = [] for i in 0..<fftResult.count { let re = fftResult[i].re let im = fftResult[i].im let magnitude = sqrt(re * re + im * im) if i == 0 { // 直流成分 amp.append(magnitude / Float(fftResult.count)) } else { // 変動成分 amp.append(2 * magnitude / Float(fftResult.count)) } } // 周波数軸を計算 let dt = x[1] - x[0] // 時間刻み var freq: [Float] = [] for k in 0..<x.count { freq.append(Float(k) / (Float(x.count) * dt)) } // 周波数の上限を指定 let freqLimit: Float = 300.0 let limitIndex = Int(freqLimit * Float(fftResult.count) * dt) let filteredFreq = freq[..<limitIndex] let filteredAmp = amp[..<limitIndex] // プロットデータの全削除 data.removeAll() // プロットデータの追加 for i in 0..<filteredFreq.count { data.append(.init(xValue: filteredFreq[i], yValue: filteredAmp[i])) } } .alert(isPresented: $showingAlert) { Alert(title: Text("Error"), message: Text("データ点数が2の冪乗数ではありません。"), dismissButton: .default(Text("了解"))) } } } } struct ContentView_Previews: PreviewProvider { static var previews: some View { // プレビュー ContentView() } } |
先ほどもデータ数が2の冪乗数でない時の処理はしていませんが、vDSPは自動的にゼロパディングによる自由なデータ数の処理が自動的に有効になっています。しかし振幅計算時に振幅補正係数を自分で書かないといけません。今回はSwiftになれていない筆者は少し面倒だったので、2の冪乗数でないデータが渡された場合に.alert()で警告文を出し計算しないという手段をとりました。
実行結果
こちらが実行結果です。
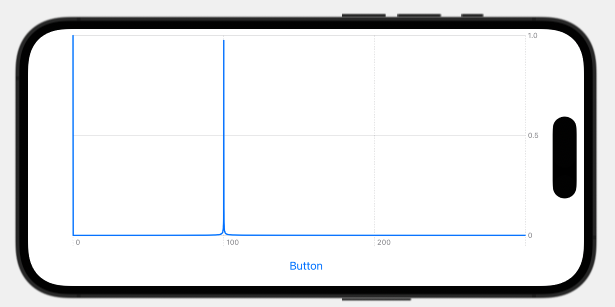
データ点数(let result = wavePoints(N: 8191, length: 10))とNを2の冪乗数でない数を指定すると、以下の図に示すメッセージを出しています。
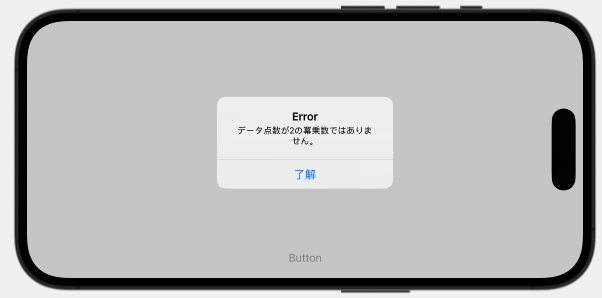
まとめ
今回はここまで!
Swiftを使ってフーリエ変換するコードを、まずはCooley-Tukey法をフルスクラッチすることで実装してみました。一度Pythonで検証していたといっても、やはりSwiftだと慣れていないので時間がかかりますね。
そして次にAccelerateというライブラリをimportし、vDSPメソッドでFFTを使ってみました。ライブラリを使うことで少し速度UPしたように感じました。
次回は録音再生アプリにFFTを実装する部分を書いてみたいと思います。
SwiftでもFFTをかけることができるようになりました!
Twitterでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています!

 ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!
ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!