ベイズの定理から最尤推定法を導出してPythonで可視化してみる

データ同化の重要な考え方である変分法の基礎、最尤推定法を学んでみます。この手法は条件付確率を示すベイズの定理を理解する必要があるため、今回も図解付きの式導出とPythonによる体験を交えて説明します。

こんにちは。wat(@watlablog)です。データ同化の基礎の続きで、最尤推定をやります！基礎なのでベイズの定理から学んでいった過程を記事にまとめました！

線形最小分散推定との違い

当ブログでは過去に「Pythonで学ぶデータ同化の基礎！線形最小分散推定をやってみる」で、1次元の変数を使ったデータ同化の基礎である線形最小分散推定を学びました。

線形最小分散推定は背景値と観測値を使って、なるべく誤差分散を小さくするように式展開を行い推定式を得ました。
まだ前回記事を読んでいない方で、線形最小分散推定をよく知らない人は是非一旦上記リンク先の記事を読んでみて下さい。

基礎知識

ベイズの定理

条件付き確率

最尤推定法は評価関数を設定して最小値を探す問題になりますが、その評価関数はベイズの定理を根拠として導出します。

何やら名前からして高度な定理を予想させますが、ベイズの定理とは単純に条件付き確率について述べているに過ぎません。ここでは簡単にベイズの定理を図解と式を用いて説明してみます。

ベイズの定理を式(1)に示します。ここで、 $p (x | y)$ が条件付き確率を示し、「 $y$ が起こった上で $x$ が起こる確率」という意味があります(同時確率ではありません)。

\begin{matrix} (1) & p (x | y) = \frac{p (y | x) p (x)}{p (y)} \end{matrix}

式(1)は左辺に書いてある「 $y$ が起こってから $x$ が起こる確率」を右辺の同じく条件付き確率「 $x$ が起こってから $y$ が起こる確率」で説明している所が特徴です。

条件付き確率の一方を原因、他方を結果と考えると、通常は原因があってから結果がわかるのに対し、式(1)は結果を使って原因の確率を分析する事ができる解釈ができ、この性質をデータ同化の分野では使います。

ホンマかいな？

※ベイズの定理の解釈には諸説あるそうです。

ベイズの定理の簡単な証明

定理だけ見るとよくわかりませんが、同時確率の考え方を使う事で簡単にベイズの定理の式導出が可能です。

おそらく最初に学校で習う条件付き確率は式(2)でしょう。

\begin{matrix} (2) & p (x | y) = \frac{p (x, y)}{p (y)} \end{matrix}

これは下図のように図解すると明解で、 $y$ が起こってから $x$ が起こるのだから、 $y$ の確率 $p (y)$ の中で（分母）、 $x$ と $y$ が同時に起こる確率 $p (x, y)$ （分子）という意味になっています。

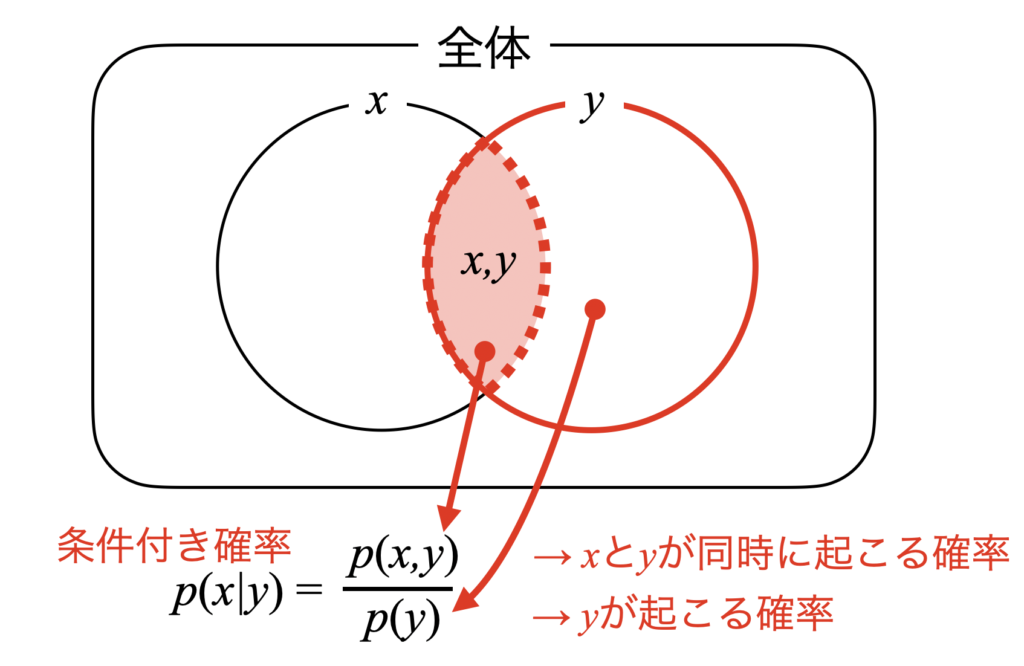
そしてこの関係は $x$ と $y$ を入れ替えても式(3)と成立します。

\begin{matrix} (3) & p (y | x) = \frac{p (x, y)}{p (x)} \end{matrix}

式(3)を図解するとこちらです。やっている事は変わらず、 $x$ が起こってから $y$ が起こるのだから、 $x$ の確率 $p (x)$ の中で（分母）、 $x$ と $y$ が同時に起こる確率 $p (x, y)$ （分子）という、当たり前の事を言っていますね。

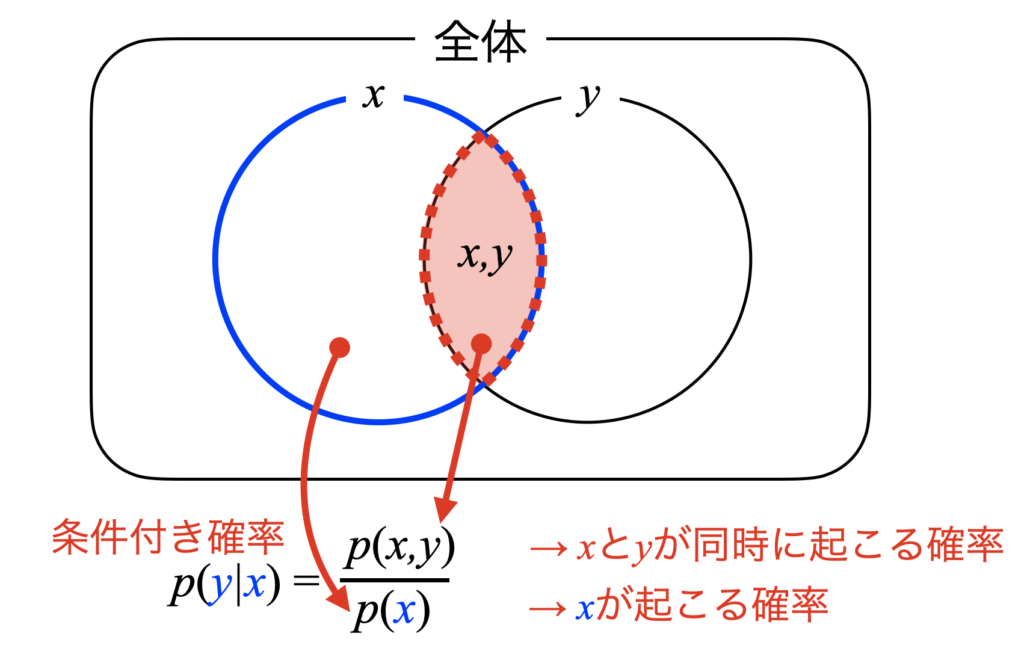
式(3)を式(4)と同時確率の式に変形し、

\begin{matrix} (4) & \begin{array}{rcl} p (y | x) & = & \frac{p (x, y)}{p (x)} \\ p (x, y) & = & p (y | x) p (x) \end{array} \end{matrix}

式(4)を式(2)の同時確率部分へ代入すると、式(1)のベイズの定理が導出されます。

以下の式は再掲。

\begin{matrix} (1) & p (x | y) = \frac{p (y | x) p (x)}{p (y)} \end{matrix}

条件付き確率の式変形でベイズの定理の式は求められるという事ですが、結果（観測）から原因の確率（分布関数）を導出する事が可能という考え方が画期的で様々な科学計算で使用されています。

ガウス分布の確率密度関数

確率密度間数の式

今回は前回の線形最小分散推定と同様にデータがガウス分布（正規分布）に従う事を仮定します。

この後の式展開でガウス分布の確率密度関数を使うため、基礎知識としてここにメモしておきましょう。

ガウス分布の確率密度関数は式(5)と、平均 $μ$ と分散 $σ^{2}$ を用いて描く事ができます。

\begin{matrix} (5) & p (x) = \frac{1}{\sqrt{2 π σ^{2}}} \exp [- \frac{(x - μ)^{2}}{2 σ^{2}}] \end{matrix}

Pythonでガウス分布の確率密度関数を描くコード

Pythonコードで実際に確率密度関数を描いて体感してみます。

以下のコードは10万点のサンプルデータをガウス分布に従うように生成して、平均と分散から確率密度関数を計算する関数gaussianを実行、生データのヒストグラムと確率密度関数を比較プロットするものです。

import numpy as np
from matplotlib import pyplot as plt

# ガウス分布を計算する関数
def gaussian(var, x_mean, x):
    p = 1 / (np.sqrt(2 * np.pi * var)) * np.exp( - ((x - x_mean) ** 2) / (2 * var))
    return p

# 10万点のサンプルデータを作成
n = np.arange(1, 100001, 1)
data = np.random.normal(loc=10, scale=15, size=len(n))

# データから平均と分散を計算してガウス分布の確率密度関数を作成
x = np.arange(-60, 61, 1)
mu = np.mean(data)                       # 平均
var = np.std(data) ** 2                  # 分散
p = gaussian(var=var, x_mean=mu, x=x)    # ガウス分布の確率密度関数を計算する
print('平均=', mu)
print('分散=', var)

# ここからグラフ描画-------------------------------------------------
# フォントの種類とサイズを設定する。
plt.rcParams['font.size'] = 14
plt.rcParams['font.family'] = 'Times New Roman'

# 目盛を内側にする。
plt.rcParams['xtick.direction'] = 'in'
plt.rcParams['ytick.direction'] = 'in'

# グラフの上下左右に目盛線を付ける。
fig = plt.figure()
ax1 = fig.add_subplot(211)
ax1.yaxis.set_ticks_position('both')
ax1.xaxis.set_ticks_position('both')
ax2 = fig.add_subplot(212)
ax2.yaxis.set_ticks_position('both')
ax2.xaxis.set_ticks_position('both')

# 軸のラベルを設定する。
ax1.set_xlabel('x')
ax1.set_ylabel('count')
ax2.set_xlabel('x')
ax2.set_ylabel('p')

# データプロット
ax1.hist(data, bins=50, range=(-60, 60), histtype='step', color='blue', label='Histogram')
ax2.plot(x, p, color='blue', label='Probability density distribution')

# グラフを表示する。
ax1.legend()
ax2.legend()
fig.tight_layout()
plt.show()
plt.close()
# -------------------------------------------------------------------

import numpy as np

from matplotlib import pyplot as plt

# ガウス分布を計算する関数

def gaussian(var, x_mean, x):

p = 1 / (np.sqrt(2 * np.pi * var)) * np.exp( - ((x - x_mean) ** 2) / (2 * var))

return p

# 10万点のサンプルデータを作成

n = np.arange(1, 100001, 1)

data = np.random.normal(loc=10, scale=15, size=len(n))

# データから平均と分散を計算してガウス分布の確率密度関数を作成

x = np.arange(-60, 61, 1)

mu = np.mean(data) # 平均

var = np.std(data) ** 2 # 分散

p = gaussian(var=var, x_mean=mu, x=x) # ガウス分布の確率密度関数を計算する

print('平均=', mu)

print('分散=', var)

# ここからグラフ描画-------------------------------------------------

# フォントの種類とサイズを設定する。

plt.rcParams['font.size'] = 14

plt.rcParams['font.family'] = 'Times New Roman'

# 目盛を内側にする。

plt.rcParams['xtick.direction'] = 'in'

plt.rcParams['ytick.direction'] = 'in'

# グラフの上下左右に目盛線を付ける。

fig = plt.figure()

ax1 = fig.add_subplot(211)

ax1.yaxis.set_ticks_position('both')

ax1.xaxis.set_ticks_position('both')

ax2 = fig.add_subplot(212)

ax2.yaxis.set_ticks_position('both')

ax2.xaxis.set_ticks_position('both')

# 軸のラベルを設定する。

ax1.set_xlabel('x')

ax1.set_ylabel('count')

ax2.set_xlabel('x')

ax2.set_ylabel('p')

# データプロット

ax1.hist(data, bins=50, range=(-60, 60), histtype='step', color='blue', label='Histogram')

ax2.plot(x, p, color='blue', label='Probability density distribution')

# グラフを表示する。

ax1.legend()

ax2.legend()

fig.tight_layout()

plt.show()

plt.close()

# -------------------------------------------------------------------

結果は下図です。ヒストグラムと確率密度関数を描く事が出来ました。

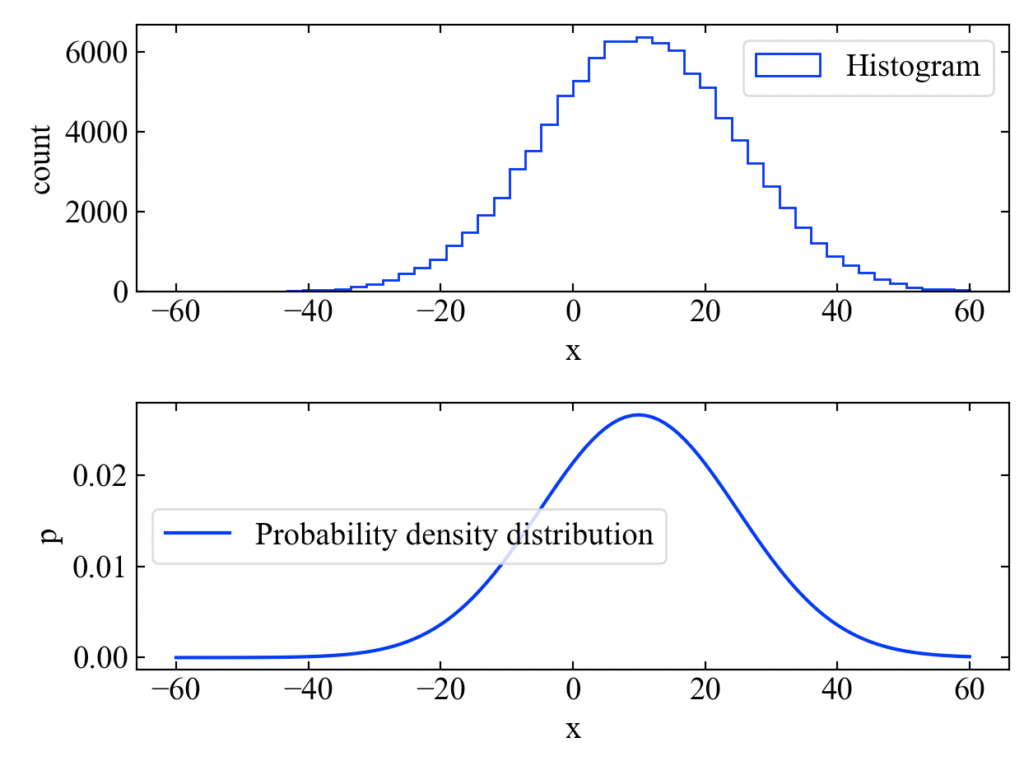
基礎知識はここらへんで十分です。それでは最尤推定法について学んでいきましょう！

最尤推定法の式導出

ここから最尤推定法の考え方、式展開を説明していきます。

条件付き確率(観測値入手)とその仮定

データ同化の技術は、観測値 $x_{o}$ が手に入った時に、背景情報を更新してより信頼性の高い推定をする所がキーになります。

そのため、ここでは観測値を入手したという条件付き確率を設定します。

そして最小分散推定を行なった時と同様に、以下の仮定を置きます。

観測値と背景値はガウス分布に従う。
観測値と背景値は共に不偏推定量である。
→期待値は母集団の平均値になる。
観測値と背景値は共に独立している。

このような仮定のもと、観測値 $x_{o}$ が手に入った時の物理量 $x$ の条件付き確率は式(1)のベイズの定理から式(6)と書く事が可能です。

\begin{matrix} (6) & p (x | x_{o}) = \frac{p (x_{o} | x) p (x)}{p (x_{o})} \end{matrix}

ここで、式(6)の意味を下図で少し見てみます。まず、左辺の条件付き確率は観測値 $x_{o}$ が手に入った後の確率分布を意味するので事後確率と呼びます。さらに、 $p (x)$ は観測も何も無い時の物理量 $x$ に対する確率分布を意味し、これを事前確率と呼びます。

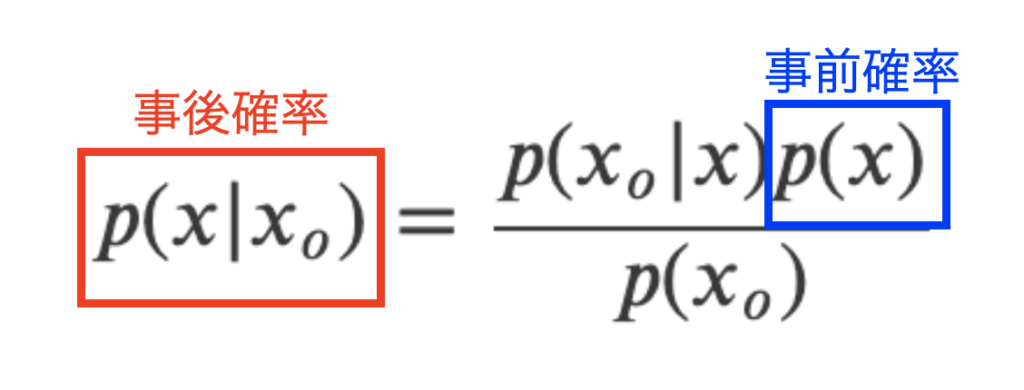
尤度関数の考え方

式(6)において既に観測値 $x_{o}$ は手に入っているため $p (x_{o})$ は定数と見なす事が出来ます。

最終的に最尤推定で求めたい量は、 $p (x | x_{o})$ の確率を最大とする位置 $x$ であるため、 $p (x_{o})$ を定数と見なす事で分子である $p (x_{o} | x) p (x)$ を最大化すれば良いという意味になります。

そのため、尤もらしさを表す尤度関数 $L$ は式(7)と書きます。
※ $L$ はLikelifoodから来ています。

\begin{matrix} (7) & L (x | x_{o}) = p (x_{o} | x) p (x) \end{matrix}

評価関数を導出する

式(7)で最大化したい関数を導出できたので、後は対応する確率密度分布 $p (x)$ と $p (x_{o} | x)$ をそれぞれ設定して積をとれば良い事になります。

$p (x)$ の確率密度関数

まずは $p (x)$ ですが、この確率密度分布は事前確率と呼ばれるもので、通常は観測値が無い中でシミュレーションモデル等による予測値（背景値）を意味します。

データはガウス分布を仮定しているため、背景値 $x_{b}$ とその分散 $σ_{b}^{2}$ を使って式(8)と表現する事が可能です。ここでは未知である真値を $x$ と置いています。仮定で不偏推定量を設定しているので、 $x_{b}$ の期待値が真値 $x$ と等しくなります。

\begin{matrix} (8) & p (x) = \frac{1}{\sqrt{2 π σ_{b}^{2}}} \exp [- \frac{(x - x_{b})^{2}}{2 σ_{b}^{2}}] \end{matrix}

$p (x_{o} | x)$ の確率密度関数

続いて $p (x_{o} | x)$ は式(9)で表現します。この式は観測値 $x_{o}$ も不偏推定量を仮定しているため、真値 $x$ が仮に得られたとした場合の観測値 $x_{o}$ の条件付き確率 $p (x_{o} | x)$ は、観測値 $x_{o}$ の平均値が未知である真値 $x$ と一致するように式を立てた…という意味合いと考えられます。

\begin{matrix} (9) & p (x_{o} | x) = \frac{1}{\sqrt{2 π σ_{o}^{2}}} \exp [- \frac{(x - x_{o})^{2}}{2 σ_{o}^{2}}] \end{matrix}

この式(9)の物理的意義に関する理解はまだ曖昧なので、もしかしたら変な事を言っているかも知れません。今は「本当はわからないけど、 $x$ が得られた場合に観測値 $x_{o}$ がわかる確率はこう設定します」というモデル化的な式なのでは？という理解です。

二つの確率密度関数の積を計算する

得られた式(8)と式(9)を式(7)に代入する事で、式(10)と尤度関数をそれぞれのデータと分散を使ってガウス分布の形で表現する事ができました。

ずいぶん複雑な関数同士の積を計算したと思いますが、単純にルートが取れる形になっている事と、 $\exp (x_{1}) \exp (x_{2}) = \exp (x_{1} + x_{2})$ である事から、途中式が必要無いくらいの簡単な計算で求める事が出来ます。

\begin{matrix} (10) & \begin{array}{rcl} L (x | x_{o}) & = & p (x_{o} | x) p (x) \\ = & (\frac{1}{\sqrt{2 π σ_{b}^{2}}} \exp [- \frac{(x - x_{b})^{2}}{2 σ_{b}^{2}}]) (\frac{1}{\sqrt{2 π σ_{o}^{2}}} \exp [- \frac{(x - x_{o})^{2}}{2 σ_{o}^{2}}]) \\ = & \frac{1}{2 π σ_{o} σ_{b}} \exp [- (\frac{(x - x_{b})^{2}}{2 σ_{b}^{2}} + \frac{(x - x_{o})^{2}}{2 σ_{o}^{2}})] \end{array} \end{matrix}

ここで以下の赤線で囲った部分は $\exp$ の中身になるので、確率密度関数を最大にするためにはこの部分を最小にすれば良いとなります。

※補足：ここで今回は尤度関数を置きましたが、ベイズの定理に則って $p (x | x_{o}) =$ の形で式展開をした方が王道かも知れません。その場合は $\exp$ の手前の係数に確率密度が来るだけですが、結論は変わりません（個人的には尤度関数の説明の方がしっくりと来たのでこの説明にしてみましたが（言い訳）…数学的にはちょっとおかしい事を言っているかも？）。

そのため式(11)と評価関数を置き、この式の最小化問題を考えます。ここで、あくまで真値がわかるわけではなく、最小化問題を解いた結果は観測値 $x_{o}$ と背景値 $x_{b}$ から推定される解析値である事を明示するために、 $x = x_{a}$ としておきます。

\begin{matrix} (11) & J (x_{a}) = \frac{(x_{a} - x_{b})^{2}}{2 σ_{b}^{2}} + \frac{(x_{a} - x_{o})^{2}}{2 σ_{o}^{2}} \end{matrix}

評価関数の微分から解析値を求める

評価関数 $J (x_{a})$ の最小値を求めるため、式(12)のように、式(11)を $x_{a}$ で微分して0と置きます。
式を展開していく事で観測値と背景値から求められた解析値 $x_{a}$ を求める事が出来ます。式展開は合成関数の微分と、合成抵抗を計算する時に使うような和分の積とかしか使っていないので高校数学の範疇だと思います。

\begin{array}{rcl} \frac{d J (x_{a})}{d x_{a}} = \frac{1}{σ_{b}^{2}} (x_{a} - x_{b}) + \frac{1}{σ_{o}^{2}} (x_{a} - x_{o}) & = & 0 \\ \frac{1}{σ_{b}^{2}} x_{a} - \frac{1}{σ_{b}^{2}} x_{b} + \frac{1}{σ_{o}^{2}} x_{a} - \frac{1}{σ_{o}^{2}} x_{o} & = & 0 \\ (\frac{1}{σ_{b}^{2}} + \frac{1}{σ_{o}^{2}}) x_{a} & = & \frac{1}{σ_{b}^{2}} x_{b} + \frac{1}{σ_{o}^{2}} x_{o} \\ (\frac{σ_{b}^{2} + σ_{o}^{2}}{σ_{b}^{2} σ_{o}^{2}}) x_{a} & = & \frac{1}{σ_{b}^{2}} x_{b} + \frac{1}{σ_{o}^{2}} x_{o} \\ (12) & x_{a} & = & \frac{σ_{o}^{2}}{σ_{b}^{2} + σ_{o}^{2}} x_{b} + \frac{σ_{b}^{2}}{σ_{b}^{2} + σ_{o}^{2}} x_{o} \end{array}

この結果は「Pythonで学ぶデータ同化の基礎！線形最小分散推定をやってみる」で求めた式(15)の解析値と等しくなります（…スゴイ）。

つまり式(13)とイノベーションを使った解析インクリメントの形にも変形する事ができるという事で、線形最小分散推定で得られる解析値の式と一致しました。これらの式はガウス分布を仮定する限り一致するという事です。

\begin{array}{rcl} x_{a} & = & \frac{σ_{o}^{2}}{σ_{b}^{2} + σ_{o}^{2}} x_{b} + \frac{σ_{b}^{2}}{σ_{b}^{2} + σ_{o}^{2}} x_{o} \\ (13) & = & x_{b} + \frac{σ_{b}^{2}}{σ_{o}^{2} + σ_{b}^{2}} (x_{o} - x_{b}) \end{array}

イノベーションと解析インクリメントは下図。背景値に対して値を更新する、という意味がデータ同化の本質となるので、この形が好まれるようです。

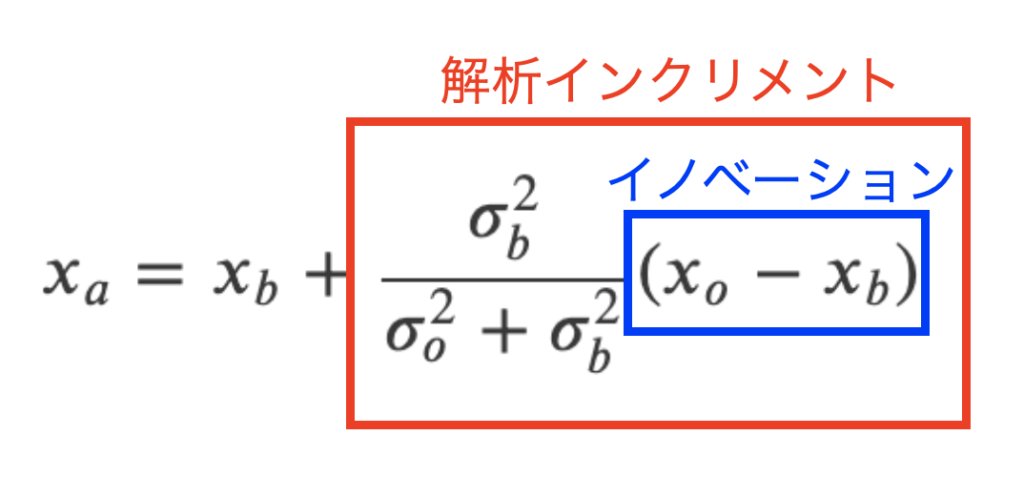
解析値の誤差分散は線形分散推定と同様に式(14)となります。

\begin{matrix} (14) & σ_{a}^{2} = \frac{σ_{b}^{2} σ_{o}^{2}}{σ_{b}^{2} + σ_{o}^{2}} \end{matrix}

解析値の確率密度分布

式(5)のガウス分布の確率密度関数に、式(14)の解析値、解析値の誤差分散を代入する事で、解析値の確率密度関数式(15)を得ます。

\begin{matrix} (15) & p (x_{a}) = \frac{1}{\sqrt{2 π σ_{a}^{2}}} \exp [- \frac{(x - x_{a})^{2}}{2 σ_{a}^{2}}] \end{matrix}

それではいよいよPythonで最尤推定法の効果を見てみましょう！ただ、式(13)は前の記事と同じなので、式(15)の確率密度分布で書いてみる事とします。

Pythonで最尤推定法を体感するコード

動作環境

コードを実行した時のこちらの動作環境を参考に記載します。

Windows

Windows	OS	Windows10 64bit
	CPU	2.4[GHz]
	メモリ	4[GB]

Mac

Mac	OS	macOS Catalina 10.15.7
	CPU	1.4[GHz]
	メモリ	8[GB]

Python環境

Pythonの外部ライブラリはNumpyとmatplotlibのみを使用しています。

Python	Python 3.7.7
PyCharm (IDE)	PyCharm CE 2020.1
Numpy	1.19.0
matplotlib	3.2.2

全コード

以下のコードは「Pythonで学ぶデータ同化の基礎！線形最小分散推定をやってみる」と同様に、擬似的にモデル予測値と観測値を生成して、本ページで求めた解析値を使って確率密度関数をプロットするものです。

コピペしてすぐに動作できるよう全コードを残しています。

import numpy as np
from matplotlib import pyplot as plt

# 解析値と誤差分散を計算する関数
def linear_min_variance_estimation(x_o, x_b):
    var_o = np.std(x_o) ** 2                                # 観測誤差分散
    var_b = np.std(x_b) ** 2                                # 背景誤差分散

    x_a = x_b + (var_b / (var_o + var_b)) * (x_o - x_b)     # 解析値
    var_a = (var_b * var_o) / (var_b + var_o)               # 解析誤差分散

    return x_a, var_a

# ガウス分布を計算する関数
def gaussian(var, x_mean, x):
    p = 1 / (np.sqrt(2 * np.pi * var)) * np.exp( - ((x - x_mean) ** 2) / (2 * var))
    return p

# 観測値と背景値を10万点のサンプルデータで作成
n = np.arange(1, 100001, 1)
x_o = np.random.normal(loc=10, scale=15, size=len(n))
x_b = np.random.normal(loc=-10, scale=10, size=len(n))

# 解析値と解析誤差分散を求める関数
x_a, var_a = linear_min_variance_estimation(x_o, x_b)

# データと誤差分散からガウス分布を作成
x = np.arange(-60, 61, 1)
var_b = np.std(x_b) ** 2
var_o = np.std(x_o) ** 2
p_o = gaussian(var=var_o, x_mean=np.mean(x_o), x=x)
p_b = gaussian(var=var_b, x_mean=np.mean(x_b), x=x)
p_a = gaussian(var=var_a, x_mean=np.mean(x_a), x=x)

# ここからグラフ描画-------------------------------------------------
# フォントの種類とサイズを設定する。
plt.rcParams['font.size'] = 14
plt.rcParams['font.family'] = 'Times New Roman'

# 目盛を内側にする。
plt.rcParams['xtick.direction'] = 'in'
plt.rcParams['ytick.direction'] = 'in'

# グラフの上下左右に目盛線を付ける。
fig = plt.figure()
ax1 = fig.add_subplot(111)
ax1.yaxis.set_ticks_position('both')
ax1.xaxis.set_ticks_position('both')

# 軸のラベルを設定する。
ax1.set_xlabel('x')
ax1.set_ylabel('p')

# データプロット
ax1.plot(x, p_o, label='Observed', color='blue')
ax1.plot(x, p_b, label='Model estimation', color='green')
ax1.plot(x, p_a, label='MLE', color='red')

# グラフを表示する。
ax1.legend()
fig.tight_layout()
plt.show()
plt.close()
# -------------------------------------------------------------------

import numpy as np

from matplotlib import pyplot as plt

# 解析値と誤差分散を計算する関数

def linear_min_variance_estimation(x_o, x_b):

var_o = np.std(x_o) ** 2 # 観測誤差分散

var_b = np.std(x_b) ** 2 # 背景誤差分散

x_a = x_b + (var_b / (var_o + var_b)) * (x_o - x_b) # 解析値

var_a = (var_b * var_o) / (var_b + var_o) # 解析誤差分散

return x_a, var_a

# ガウス分布を計算する関数

def gaussian(var, x_mean, x):

p = 1 / (np.sqrt(2 * np.pi * var)) * np.exp( - ((x - x_mean) ** 2) / (2 * var))

return p

# 観測値と背景値を10万点のサンプルデータで作成

n = np.arange(1, 100001, 1)

x_o = np.random.normal(loc=10, scale=15, size=len(n))

x_b = np.random.normal(loc=-10, scale=10, size=len(n))

# 解析値と解析誤差分散を求める関数

x_a, var_a = linear_min_variance_estimation(x_o, x_b)

# データと誤差分散からガウス分布を作成

x = np.arange(-60, 61, 1)

var_b = np.std(x_b) ** 2

var_o = np.std(x_o) ** 2

p_o = gaussian(var=var_o, x_mean=np.mean(x_o), x=x)

p_b = gaussian(var=var_b, x_mean=np.mean(x_b), x=x)

p_a = gaussian(var=var_a, x_mean=np.mean(x_a), x=x)

# ここからグラフ描画-------------------------------------------------

# フォントの種類とサイズを設定する。

plt.rcParams['font.size'] = 14

plt.rcParams['font.family'] = 'Times New Roman'

# 目盛を内側にする。

plt.rcParams['xtick.direction'] = 'in'

plt.rcParams['ytick.direction'] = 'in'

# グラフの上下左右に目盛線を付ける。

fig = plt.figure()

ax1 = fig.add_subplot(111)

ax1.yaxis.set_ticks_position('both')

ax1.xaxis.set_ticks_position('both')

# 軸のラベルを設定する。

ax1.set_xlabel('x')

ax1.set_ylabel('p')

# データプロット

ax1.plot(x, p_o, label='Observed', color='blue')

ax1.plot(x, p_b, label='Model estimation', color='green')

ax1.plot(x, p_a, label='MLE', color='red')

# グラフを表示する。

ax1.legend()

fig.tight_layout()

plt.show()

plt.close()

# -------------------------------------------------------------------

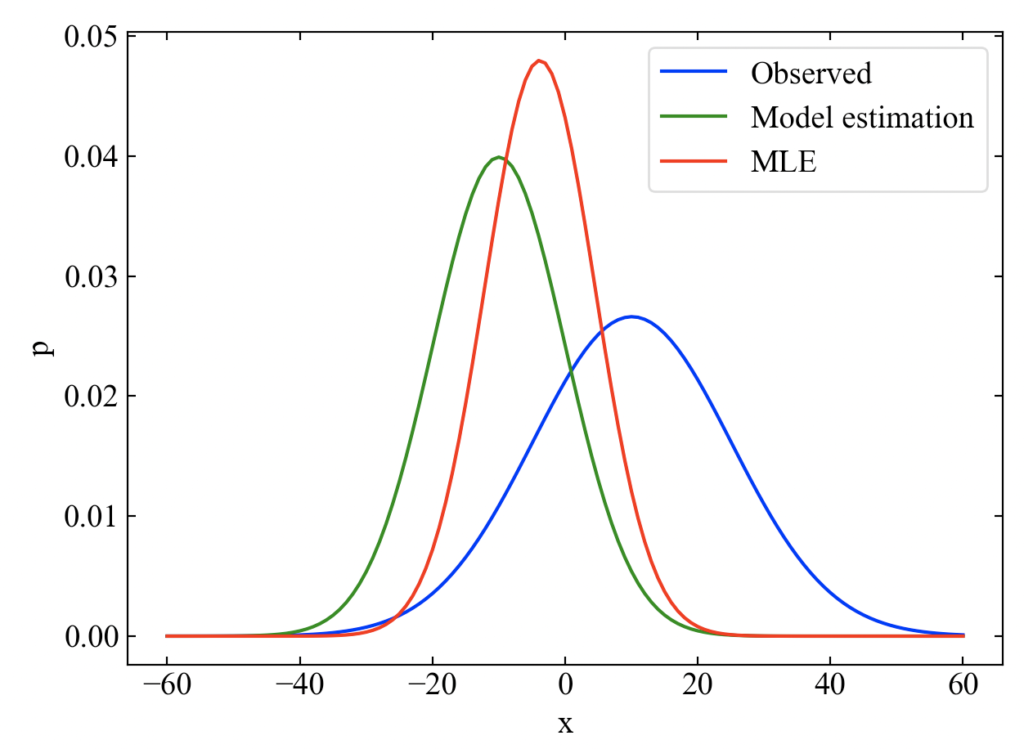
以下が結果です。全て確率密度関数で表現しています。MLEとは、Maximum Likelifood Estimation（最尤推定）を意味しています。最小分散推定と同じように推定結果の分散はモデル予測値と観測値の両方よりも小さくなっています（同じ式になっているので当たり前ですが…）。

まとめ

本記事では最尤推定法の基礎の基礎を理解するために、ベイズの定理の証明から入り、ガウス分布（正規分布）の式の紹介、最尤推定式導出までの式展開を行いました。

僕自身数学は得意ではないので、1つの教科書ではすっ飛ばしているような部分もできるだけ途中式を書くようにしてみました。

しかし学習開始間も無いため厳密な数学的表現からすると間違った書き方になっている物と推測するためご注意下さい（本記事の内容を何かに使う場合はご自分で参考書等を理解してください）。

とはいえ、最終的にはPythonによる最尤推定結果の確率密度関数プロットまでを確認する事が出来ました。

最尤推定法は変分法の基礎となっています。本記事では1次元のデータに対して基礎的な事を学んだに過ぎませんが、今後はデータ同化の技術を多次元に拡張する事ができるよう精進したいと思います。

最尤推定法と線形最小分散推定の式導出結果が一致する事を確認しました！結果が同じでも考え方が異なるというのは面白いです！
Twitterでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています！

線形最小分散推定との違い

基礎知識

ベイズの定理

条件付き確率

ベイズの定理の簡単な証明

ガウス分布の確率密度関数

確率密度間数の式

Pythonでガウス分布の確率密度関数を描くコード

最尤推定法の式導出

条件付き確率(観測値入手)とその仮定

尤度関数の考え方

評価関数を導出する

$p (x)$ の確率密度関数

$p (x_{o} | x)$ の確率密度関数

二つの確率密度関数の積を計算する

評価関数の微分から解析値を求める

解析値の確率密度分布

Pythonで最尤推定法を体感するコード

動作環境

Windows

Mac

Python環境

全コード

まとめ

コメントを残すコメントをキャンセル

最近の投稿

アーカイブ

カテゴリー

線形最小分散推定との違い

基礎知識

ベイズの定理

条件付き確率

ベイズの定理の簡単な証明

ガウス分布の確率密度関数

確率密度間数の式

Pythonでガウス分布の確率密度関数を描くコード

最尤推定法の式導出

条件付き確率(観測値入手)とその仮定

尤度関数の考え方

評価関数を導出する

p(x)の確率密度関数

p(xo|x)の確率密度関数

二つの確率密度関数の積を計算する

評価関数の微分から解析値を求める

解析値の確率密度分布

Pythonで最尤推定法を体感するコード

動作環境

Windows

Mac

Python環境

全コード

まとめ

SNSでもご購読できます。

コメントを残す コメントをキャンセル

最近の投稿

アーカイブ

カテゴリー

$p (x)$ の確率密度関数

$p (x_{o} | x)$ の確率密度関数

コメントを残すコメントをキャンセル