1. ホーム /
  2. AI /
  3. AI実装検定S級対策！「画像処理100本ノック」学習記録・カンペ
好評発売中！いきなりプログラミングPython ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました！
  • 2020.12.21

AI実装検定S級対策！「画像処理100本ノック」学習記録・カンペ

  • このエントリーをはてなブックマークに追加

第1回AI実装検定S級を受験しますが、例題が無いので出題範囲になっている「画像処理100本ノック」を学習して記録をつけます。といっても、まだまだ理解には遠くおよばず、ほんとにメモレベル！

こんにちは。wat(@watlablog)です。AI実装検定S級の勉強を始めたので、ここに学習結果を記録していきます！

AI実装検定S級の公式出題範囲は「画像処理100本ノック」と「ディープラーニング∞本ノック」の二つですが、ここでは画像処理100本ノックを学習します。

画像処理100本ノックはimori_imori(yoyoyo-yo)さんのGitHubコンテンツです。

著作権の観点から、このページでは自分で実践してみた記録のみを残していきます。ここでは各画像処理の特徴のみをメモしていきコードは転載しません。
以下に公式リンクを載せますので、コードの全貌や詳細はそちらをご覧下さい。

画像処理100本ノック：https://github.com/yoyoyo-yo/Gasyori100knock

目次（項目クリックでジャンプできます）

Q1-Q10

Q1：チャネルの入れ替え

まずは画像の色チャネル（チャンネル（Channel）とも呼ぶ？)を交換する方法です。問題はRGBの色配列で読み込んだ画像をBGRの色配列に変換せよとのこと。

OpenCVを使うと、img = cv2.cvtColor(img, cv2.COLOR_RGB2BGR)と書けますが、

numpyの配列だと、img[...,[2,1,0]]で書けて、以下のように色変換が可能です。
今回は画像処理分野で有名なカラフルゴリラ画像を.pngで用意しました。

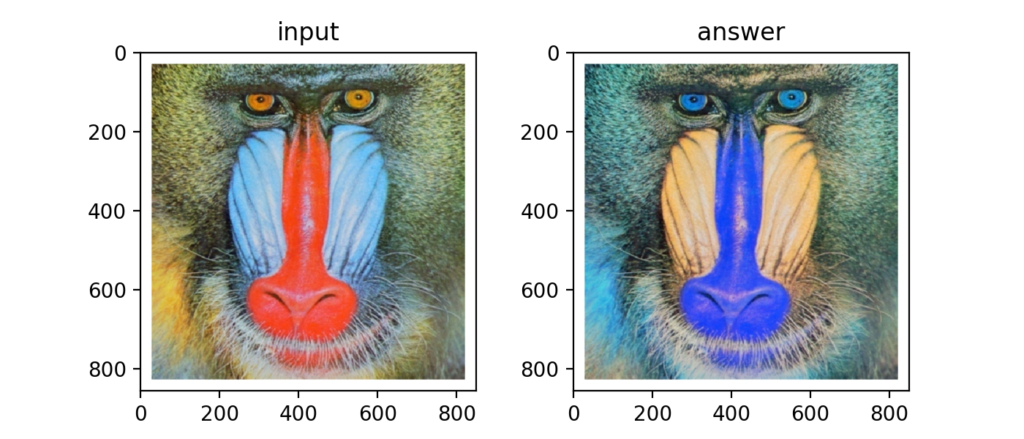
チャネル入れ替え

GitHubに載っているimg[..., ::-1]という書き方だと透明度を指定するアルファチャンネルを持つ.png画像ではうまくいきませんでした（下画像のようになってしまう）。

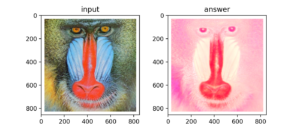
Q1失敗事例

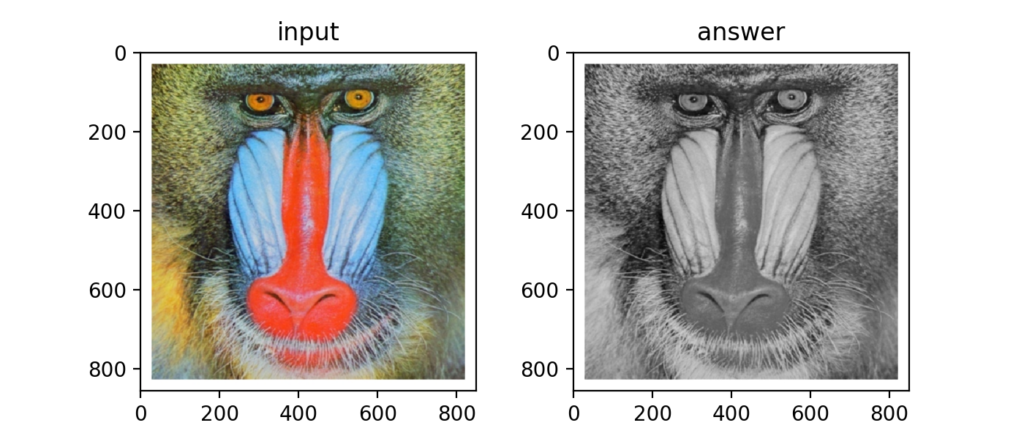
Q2：グレースケール変換

OpenCVではcv2.cvtColor(img, cv2.COLOR_RGB2GRAY)と書けば簡単にグレースケール変換が出来ていましたが…。

なんとグレースケール変換はRGBの平均値ではありませんでした（勘違いしていた）。img[..., 0] * 0.2126 + img[..., 1] * 0.7152 + img[..., 2] * 0.0722とR(0)G(1)B(2)に係数をかけて加算し、0-255にクリッピングするそうです。

グレースケール画像

np.clip(画像, 0, 255)でクリッピングできるのは初見。便利。

Q3：二値化

OpenCVによる二値化は「Python/OpenCVで画像の二値化をする方法」で扱いましたが、numpyだけで書く場合は、np.minimum(img // th, 1) * 255となります。

np.minimumや切り捨て演算子「//」を使ってエレガントに書かれていていますね。

二値化

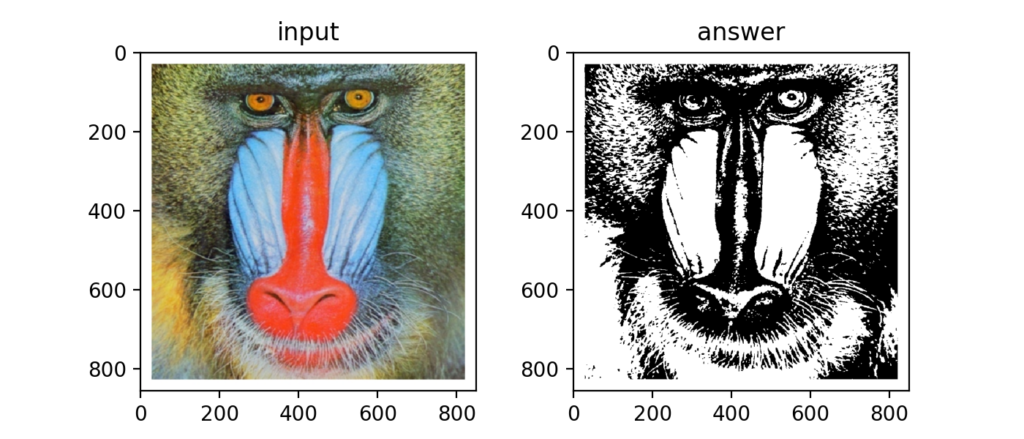
OpenCVを使う場合もそうでない場合も、グレースケール画像を使うのは共通です。

Q4：大津の二値化

大津の二値化は自動で閾値を決定することが可能な二値化アルゴリズムです。
OpenCVではcv2.threshold(img, 0,255,cv2.THRESH_BINARY+cv2.THRESH_OTSU)となります。

やっている事は画像の輝度値をヒストグラムでみた時に、クラス0、クラス1と二つのクラスを仮定して、バランス良く分離できる閾値を決定するという事です。

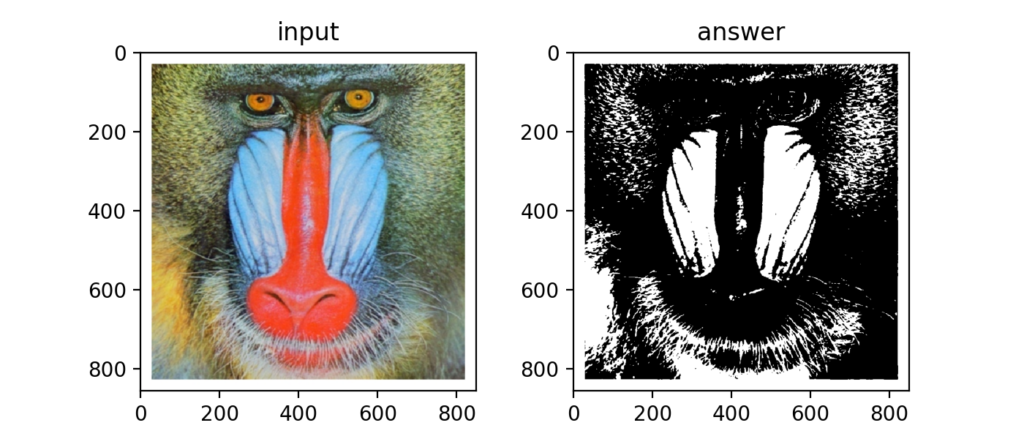
大津の二値化

自動で閾値を決定する流れは教師無し学習のクラスタリングに相当するのでは？と思いました。

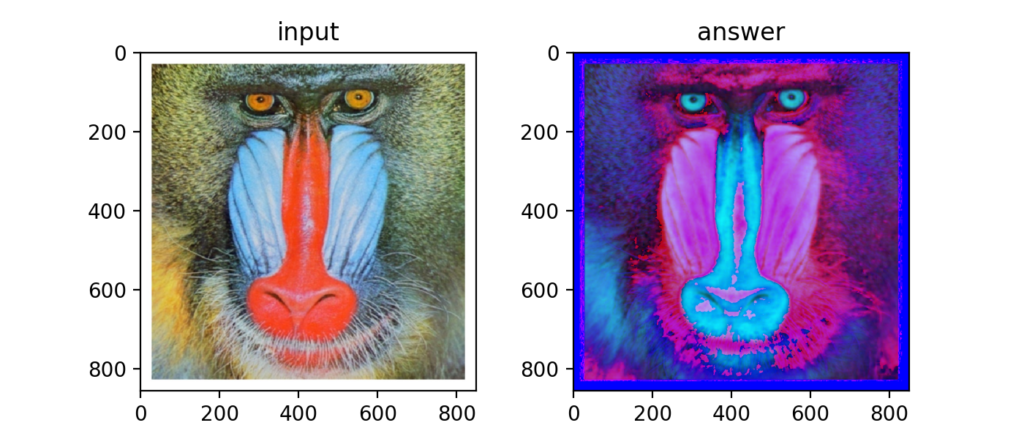
Q5：HSV変換

HSVとは、Hue(色相), Saturation(彩度), Value(明度)の事で、RGBと同じく色を指定する方法の一つです。

OpenCVを使えばcv2.cvtColor(img, cv2.COLOR_RGB2HSV)で簡単にRGB画像をHSV画像に変換する事ができますが、自力で実装する場合は以下の式（Wikiにも載っている）による変換が必要です。

\[
H=
\left\{\begin{matrix}
{\rm undefined} &({\rm if} Min = Max) \\
60 \frac{G-R}{Max-Min}+60 &({\rm if} Min = B) \\
60 \frac{B-G}{Max-Min}+180 &({\rm if} Min = R) \\
60 \frac{R-B}{Max-Min}+300 &({\rm if} Min = G)
\end{matrix}\right.\\
S=Max - Min\\
V=Max
\]

HSV変換

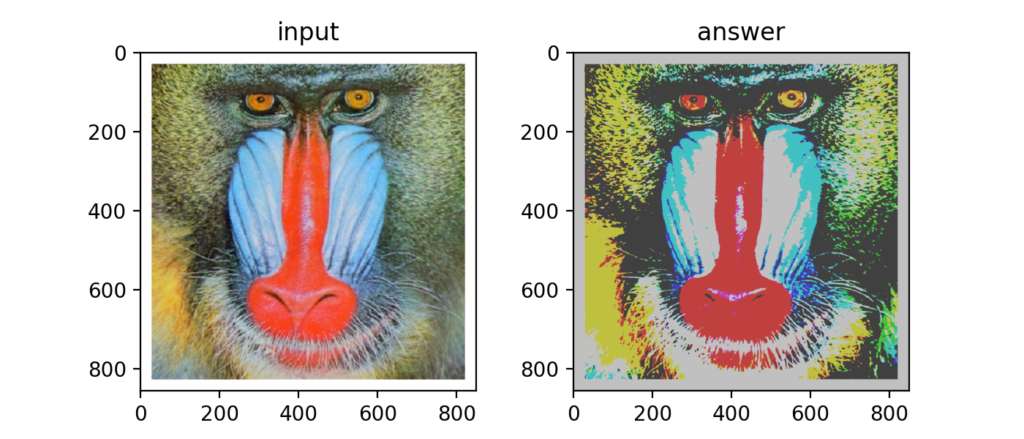
Q6：減色処理

減色処理とは、例えばRGBそれぞれ256色ある画像を4色ずつや8色ずつにするといった操作の事で、GitHubで公開されているコードでやっている事は均等に分割（量子化する）均等量子化という処理を行っています。

以下の図はRGBを各4色にまで減色したもの。

減色処理

Q7：平均プーリング

画像内に四角形の領域を考え、その領域内の全輝度値を平均した値で埋め直す事を平均プーリングと呼びます。

この平均プーリングは当ブログでも過去に似たような動作をPythonプログラムで書いた事があります（以下リンク）。

「Python/OpenCVで画像内の領域を縦横に走査する方法」

但し、GitHubに載っている例題はより効率的に書いてあり参考になりました。
平均プーリングを実行すると、以下のように元画像がぼやけたような変化をします。

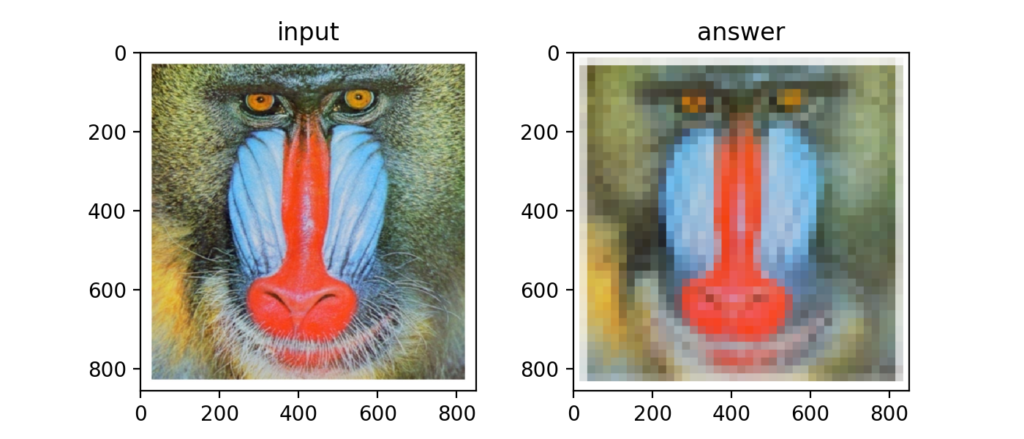
平均プーリング

この平均プーリングはディープラーニングで、特にCNNのアルゴリズムで重要な処理となっています。

Q8：最大プーリング

上記平均プーリングを、平均値ではなく最大値で行うと、それは最大プーリングになります。

最大プーリング

Q9：ガウシアンフィルタ

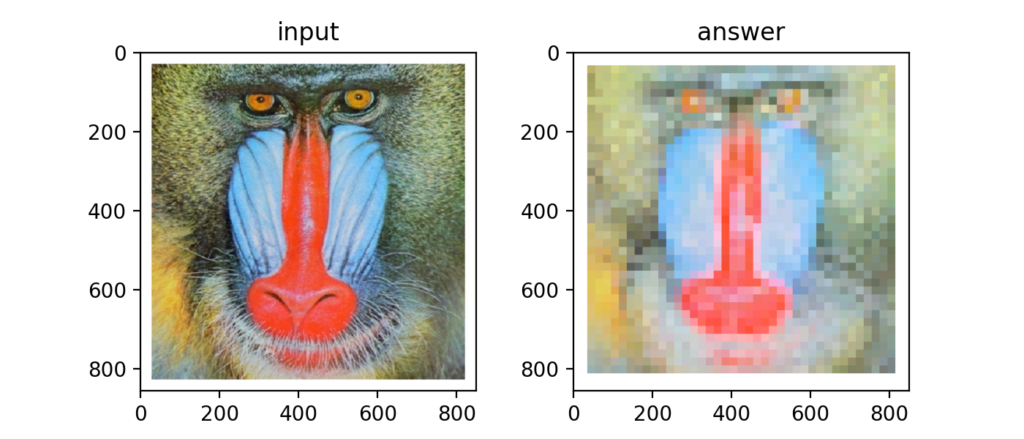
画素の周辺をガウス分布で平滑化し、ノイズを除去するフィルタをガウシアンフィルタと呼びます。

以下のカーネルと呼ばれる重みで、ガウス分布で計算します。

\[
k(x,y)=\frac{1}{2 \pi \sigma^{2}}e^{-\frac{x^{2}+y^{2}}{2 \sigma{2}}}
\]

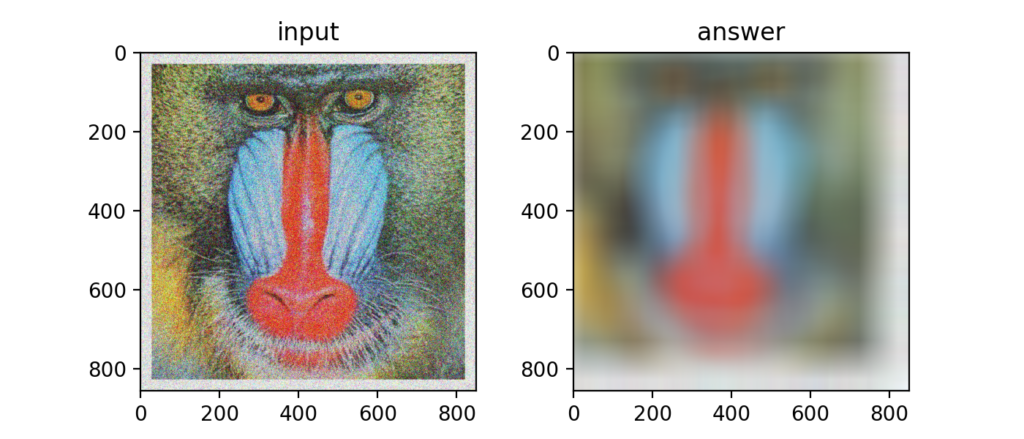
ガウシアンフィルタ

これはやりすぎ。

Q10：メディアンフィルタ

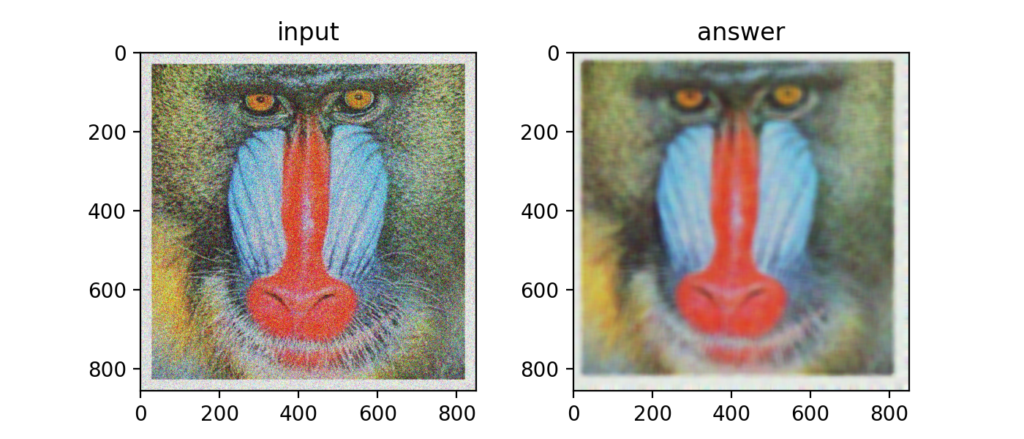
平均値、最大値の他に中央値（メディアン）を使うフィルタをメディアンフィルタと呼びます。

ある領域の中央値をあてがうという事でノイズの軽減につながります。

メディアンフィルタ

Q11-Q20

Advertisements

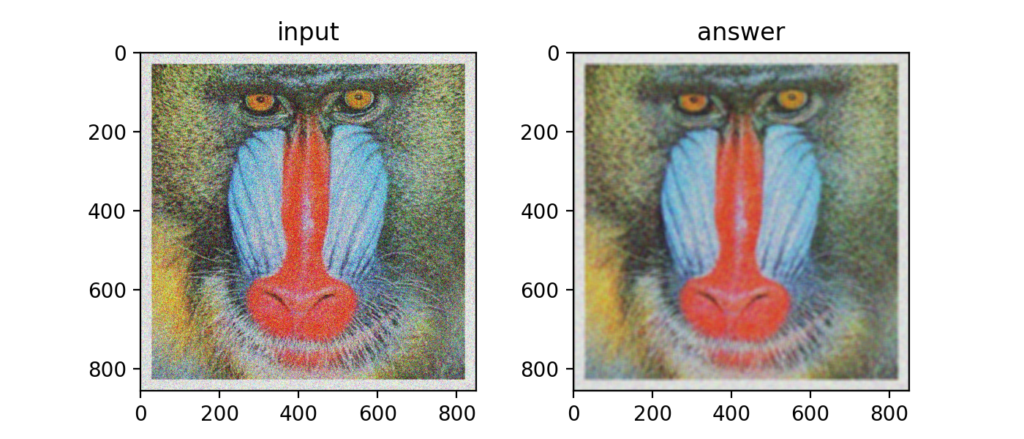
Q11：平滑化フィルタ

フィルタ内の画素の平均を使う平滑化フィルタを使ってもノイズを軽減する事ができます。

平滑化フィルタ

Q12：モーションフィルタ

対角方向の平均化を行うフィルタにモーションフィルタという物もあるとの事。

3×3のサイズであればカーネルは以下の式になります。

\[
K=\begin{bmatrix}
\frac{1}{3} & 0&0 \\
0&\frac{1}{3} & 0\\
0& 0&\frac{1}{3}
\end{bmatrix}
\]

モーションフィルタ

…正直僕にはあまり平滑化フィルタとの違いがわからない。

Q13：Max-Minフィルタ

フィルタ内の最大値と最小値の差を求めるMax-Minフィルタを使うと、下図のようにエッジ検出に使う事ができます。

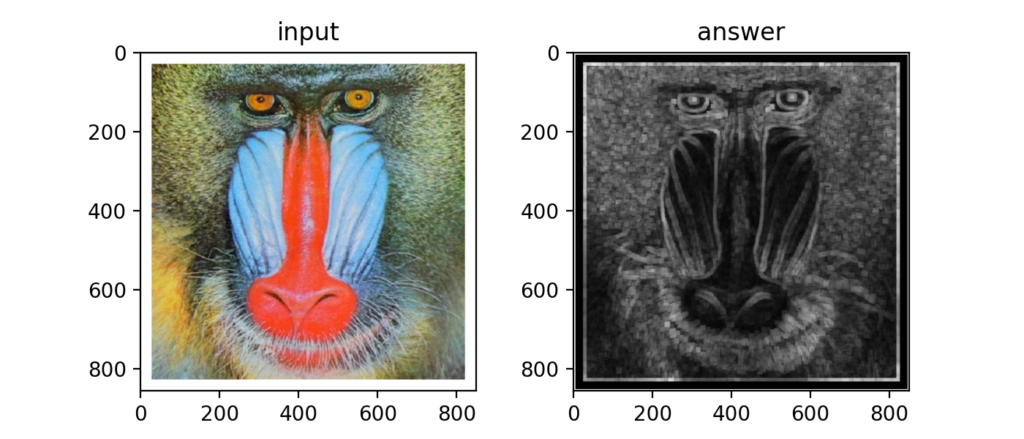
Max-Minフィルタ

Q14：微分フィルタ

カーネルを縦方向\(K_{v}\)と横方向\(K_{h}\)を設定すると、微分フィルタと呼ばれるフィルタになります。

\[
K_{v}=\begin{bmatrix}
0 & -1&0 \\
0&1 & 0\\
0& 0&0
\end{bmatrix},
K_{h}=\begin{bmatrix}
0 & 0&0 \\
-1&1 & 0\\
0& 0&0
\end{bmatrix}
\]

微分は傾きを求める事で有名ですが、急峻な変化を抽出する事ができるため、これもエッジ検出に使われます。

下図がその結果、元画像と縦と横の微分画像を並べてみました…が、ちょっとよくわかりません。

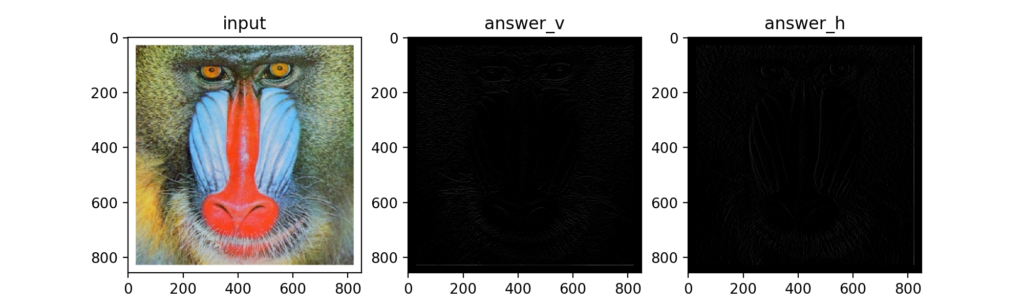
微分フィルタ1

微分フィルタ後の画像の輝度値をちょっといじってみると、確かにエッジを検出できているみたいです。

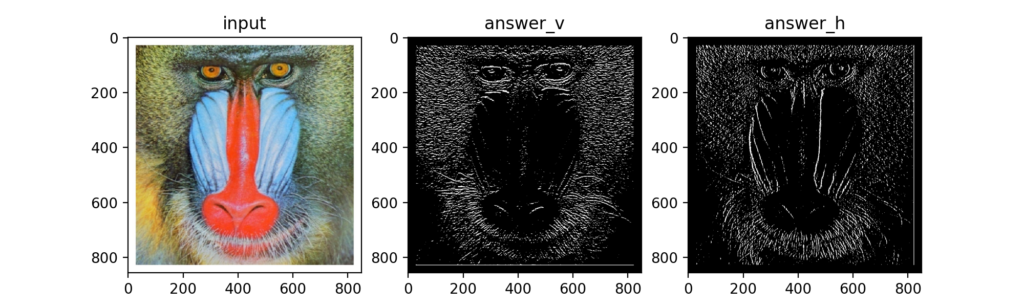
微分フィルタ2

Q15：Prewittフィルタ

微分フィルタを拡張し、以下のカーネルにするとPrewittフィルタになります。こちらもエッジ検出目的。

\[
K_{v}=\begin{bmatrix}
1&1&1 \\
0&0&0\\
-1&-1&-1
\end{bmatrix},
K_{h}=\begin{bmatrix}
1&0&-1 \\
1&0&-1\\
1&0&-1
\end{bmatrix}
\]

特に輝度値をいじらなくてもエッジを視認できました。先ほどの微分フィルタよりは感度が良いようです。

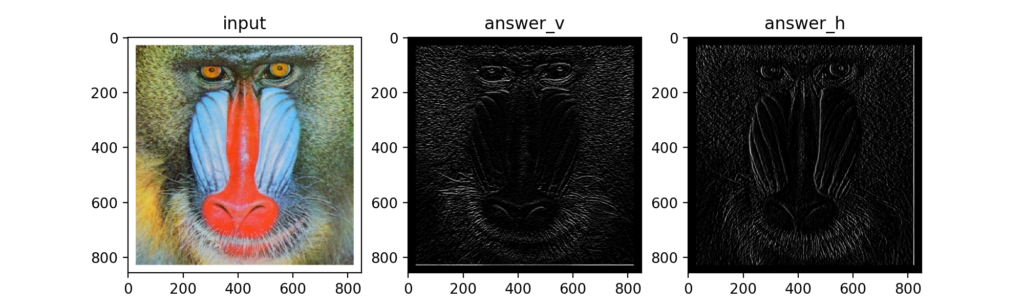
Prewittフィルタ

Q16：Sobelフィルタ

Prewittフィルタのカーネル中心部に重みを付けるとSobelフィルタになります。これはよく聞くので結構有名かも？

\[
K_{v}=\begin{bmatrix}
1&2&1 \\
0&0&0\\
-1&-2&-1
\end{bmatrix},
K_{h}=\begin{bmatrix}
1&0&-1 \\
2&0&-2\\
1&0&-1
\end{bmatrix}
\]

下図のようにエッジを検出できました。

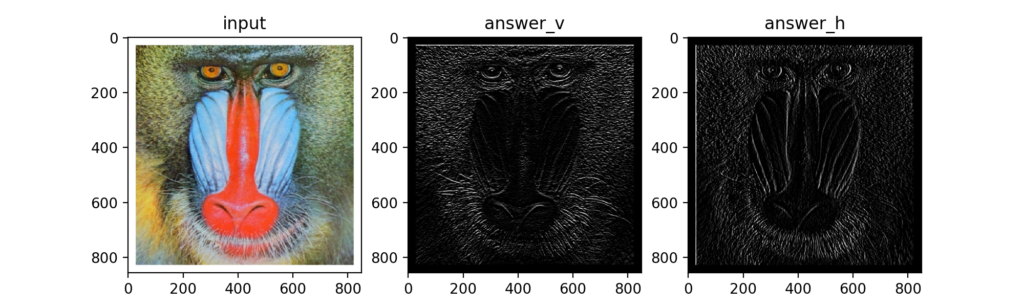
Q17：Laplacianフィルタ

2階微分のカーネルを設定するとLaplacianフィルタとなり、こちらもエッジを検出するために使われます。

\[
K=\begin{bmatrix}
0&1&0 \\
1&-4&1\\
0&1&0
\end{bmatrix}
\]

微分フィルタと同じくデフォルト設定ではエッジがよくわかりませんが…、

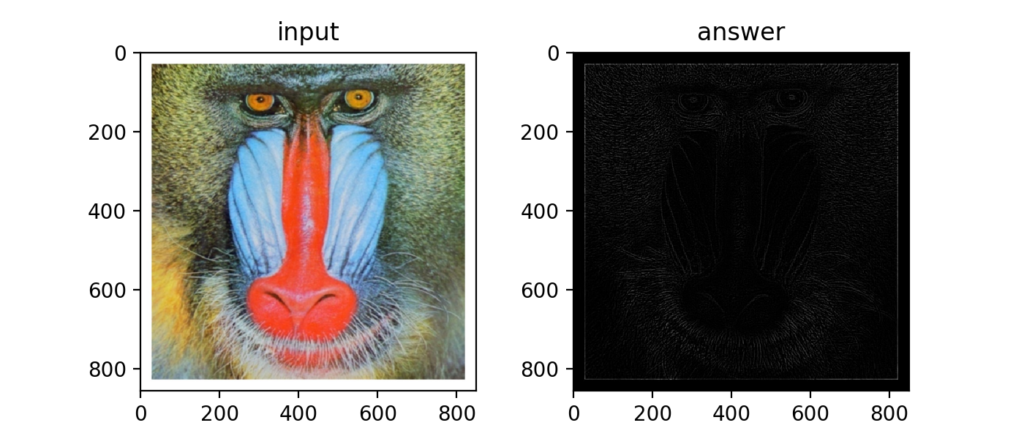
Laplacianフィルタ1

輝度値を調整すると以下のようになります。カーネル1つで良いのが便利…なのでしょうか？

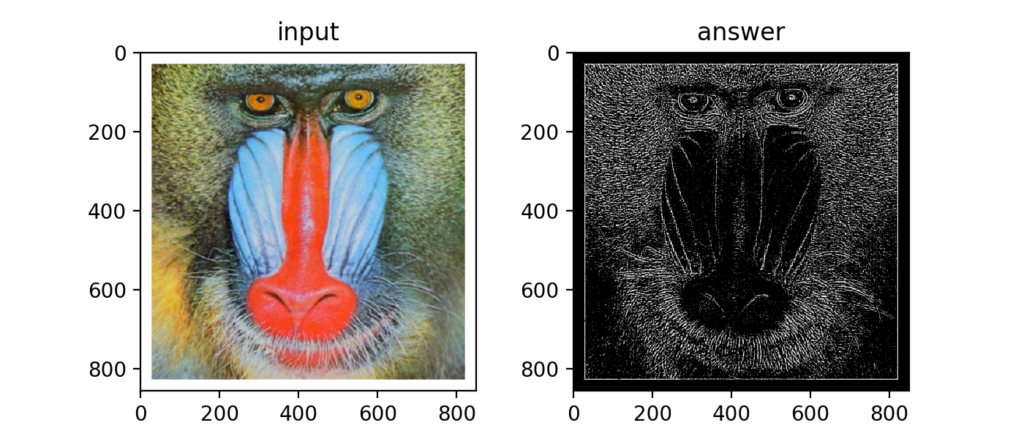
Laplacianフィルタ2

Q18：Embossフィルタ

以下のカーネルを使うとEmbossフィルタと呼ばれる輪郭を浮き出ささせるフィルタになります。

\[
K=\begin{bmatrix}
-2&-1&0 \\
-1&1&1\\
0&1&2
\end{bmatrix}
\]

下図が結果。これははっきり効果がわかりますね。

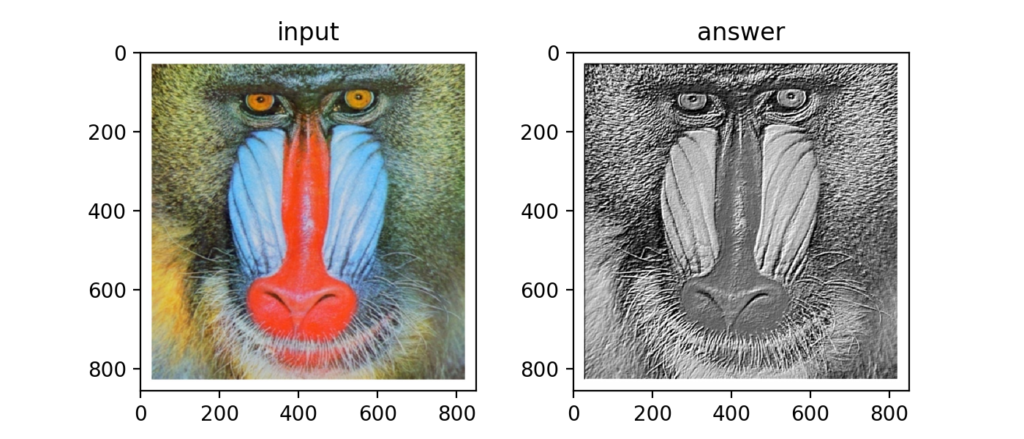
Embossフィルタ

Q19：LoGフィルタ

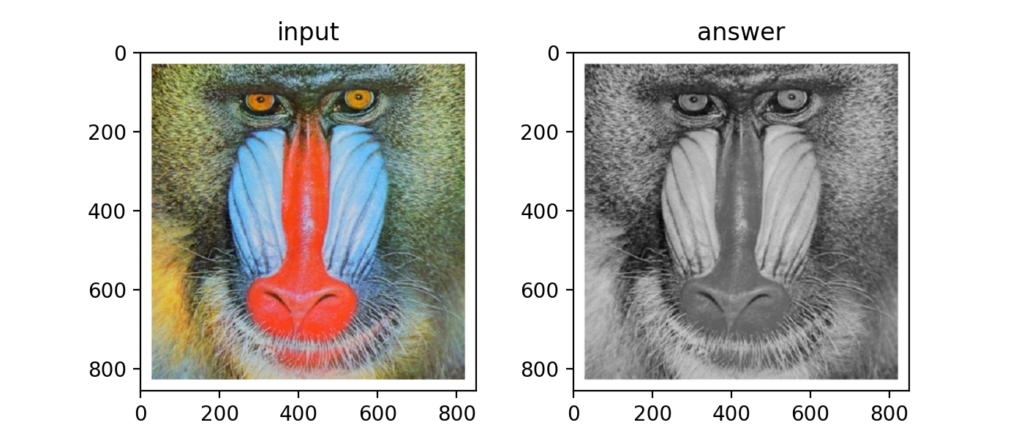
LoG（Laplacian of Gaussian）フィルタとは、Gaussianフィルタを行ってノイズ除去を行った後にLaplacianフィルタで輪郭を検出するものです。式は以下です。

\[
LoG = \nabla^{2}G=(\frac{\partial^2 }{\partial x^2}+\frac{\partial^2 }{\partial y^2})G=\frac{x^{2}+y^{2}-2\sigma^{2}}{2\pi\sigma^{6}}e^{-\frac{x^{2}+y^{2}}{2 \sigma^{2}}}
\]

LoGフィルタ

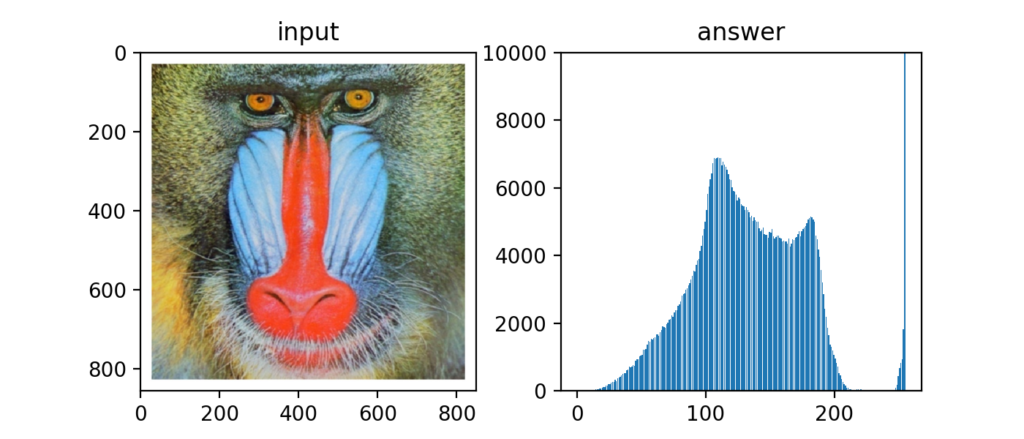
Q20：ヒストグラム表示

画像のヒストグラムもmatplotlibなら簡単に計算する事ができます。

Q21-Q30

Q21：ヒストグラム正規化

画像のヒストグラムの偏りを調整するためにはヒストグラム正規化を行います。

例えば、以下の結果は輝度値がほぼ0-255の範囲に分布している元画像を、100-255の分布に正規化した結果です。これはわかりやすいですね。

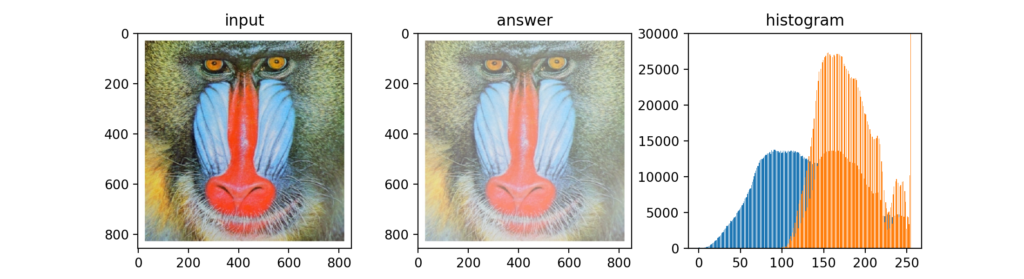
ヒストグラム正規化

c-dの範囲の画像をa-bの範囲に正規化するために以下の式を使います。

\[
x_{out}=\left\{\begin{matrix}
a&[x_{in}< c] \\
\frac{b-a}{d-c}(x_{in}-c)&[c\leq x_{in}<d]\\
b&[other]
\end{matrix}\right.
\]

Q22：ヒストグラム調整（平均と標準偏差）

上記はヒストグラム範囲の調整でしたが、ヒストグラムの平均と標準偏差の調整は以下の式で行います。この式は元画像の輝度値平均\(m\)と標準偏差\(s\)を、\(m_{0}\)と\(s_{0}\)に変換する事が出来ます。

\[
x_{out}=\frac{s_{0}}{s}(x_{in}-m)+m_{0}
\]

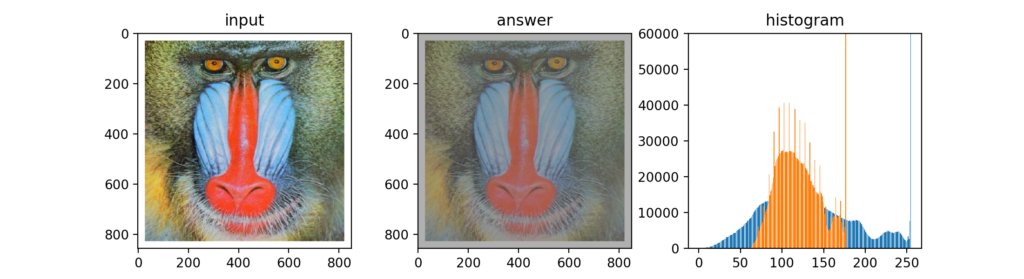
ヒストグラム調整

Q23：ヒストグラム平坦化

ヒストグラム平坦化（Histogram Equalization）を行う事でヒストグラムの均衡にする事が出来ます。この操作は平均や標準偏差といった数値を使わない事が特徴との事。

画素値総数\(S\)、画素値最大値\(Z_{max}\)、iの度数\(h(i)\)とすると、次式で計算されます。

\[
{Z}'=\frac{Z_{max}}{S}\sum_{i=0}^{z}h(i)
\]

薄い画像（ヒストグラムが高い輝度値に分布）に対して平坦化を行った結果がこちら。いい感じの色合いになりました。

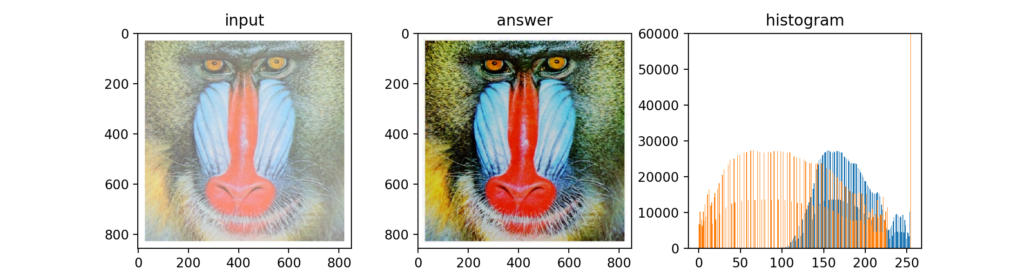
ヒストグラム平坦化

Q24：ガンマ補正

ガンマ補正（Gamma correction）とは、撮影時等に本来の色から非線形的に輝度値が変化してしまった場合の補正に使われます。非線形で発生する変化を次式で補正します（詳細はGitHubをご覧下さい）。

\[
x_{out}=(\frac{1}{c}x_{in})^\frac{1}{\gamma}
\]

\(c\)と\(\gamma\)を調整して使います。

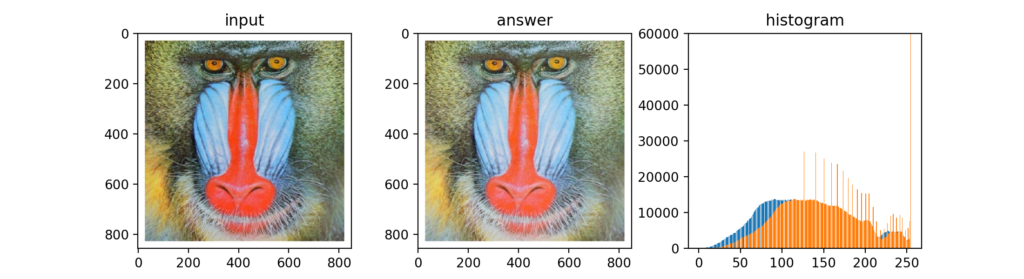
Q25：最近傍補間による拡大

画像の拡大方法として最近傍補間（Nereset Neighbor interpolation）あります。拡大する時に周りの画素値を最も近い画素値を使って埋めるという方法で、あまり綺麗にはなりませんが、次式のようなシンプルな考え方をします。

\[
{I}'(x, y)=I(round(\frac{x}{ax}), round(\frac{y}{ay}))
\]

以下は画像サイズを1.5倍にしてみた結果です（グラフの縦横数値をご覧下さい）。このくらいだったら解像度の悪さは全く気にならないレベルですね。

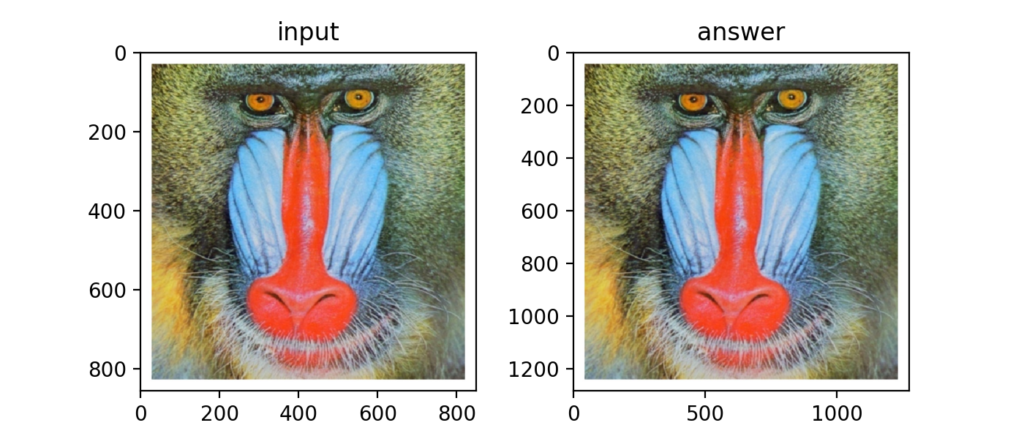
最近傍補間

Q26：Bi-Linear補間による拡大

Bi-Linear補間を使うと周辺4要素の情報を使って補間する事ができます。先ほどの最近傍補間よりも滑らかな拡大が可能。

\[ {I}'(x, y)=(1-dx)(1-dy)I(x,y)+dx(1-dy)I(x+1, y)+(1-dx)dyI(x, y+1)+dxdyI(x+1, y+1) \]

ちょっと滑らかに…わからないか。

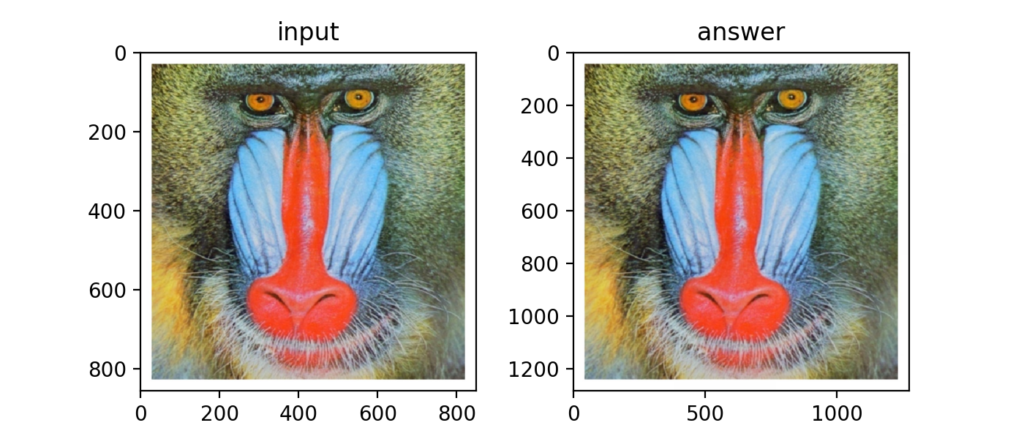
Bi-Linear補間

Q27：Bi-Cubic補間による拡大

Bi-Cubic補間はBi-Linear補間の拡張で周辺16要素の情報を使って画像を拡大するためさらに滑らかになります（式は省略）。

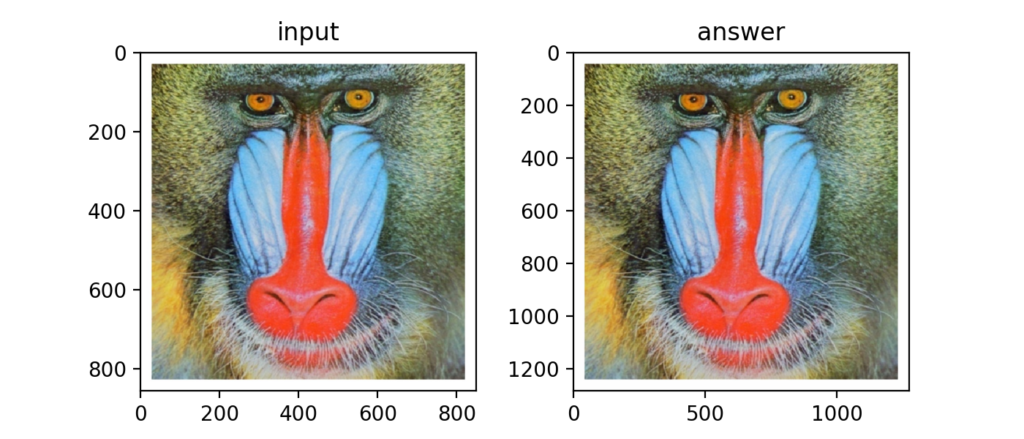
Bi-Cubic補間

Q28：アフィン変換(平行移動）

アフィン変換は画像の変形を行う変換です。次式が平行移動に関するアフィン変換の式です。2D平面のベクトル操作と同じですね。

\[
\begin{bmatrix}
{x}'\\
{y}'\\
1\end{bmatrix}=
\begin{bmatrix}
a &b &tx \\
c &d &ty \\
0 &0 &1
\end{bmatrix}
\begin{bmatrix}
x\\
y\\
1
\end{bmatrix}
\]

画像が平行移動した事を確認。

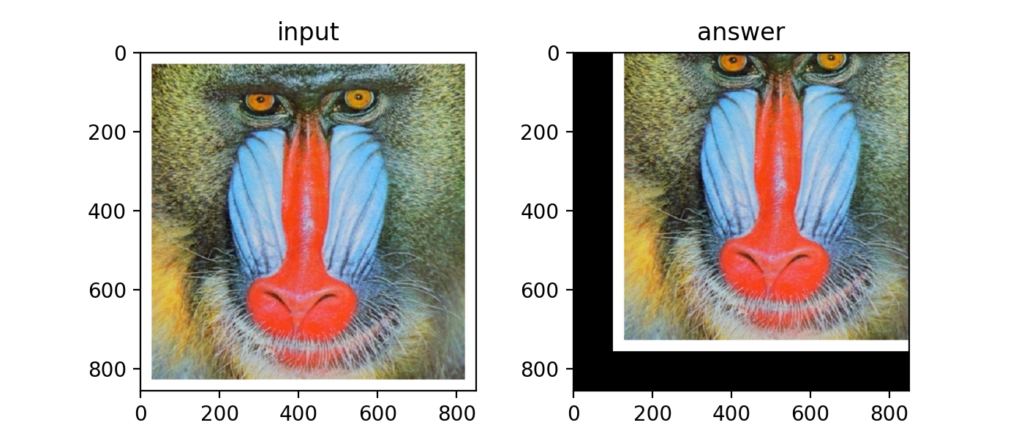
アフィン変換（平行移動）

Q29：アフィン変換(拡大縮小）

先ほどの式のabcdをそれぞれ倍率としていじることで拡大縮小が可能です。

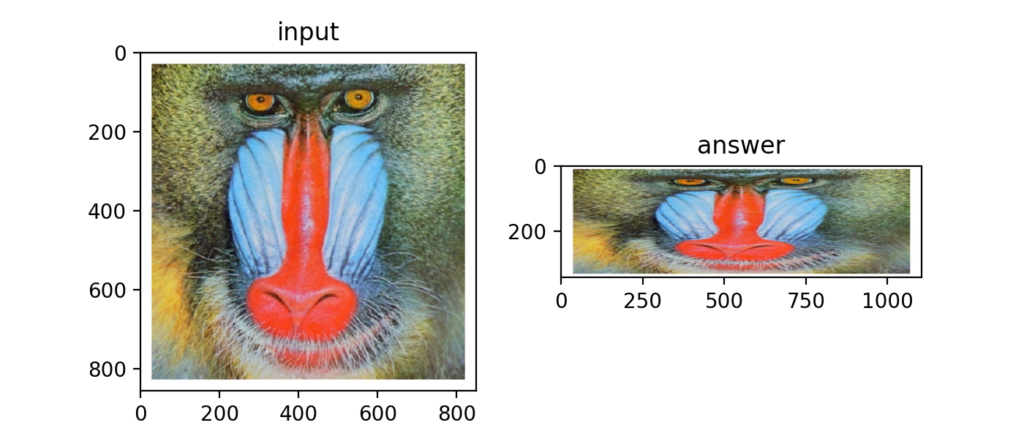
アフィン変換（拡大縮小）

Q30：アフィン変換(回転移動）

次式は回転のアフィン変換。これもベクトル操作でおなじみですね。これは僕も仕事でよく使います。

\[
\begin{bmatrix}
{x}'\\
{y}'\\
1\end{bmatrix}=
\begin{bmatrix}
\cos \theta &-\sin \theta &tx \\
\sin \theta &\cos \theta &ty \\
0 &0 &1
\end{bmatrix}
\begin{bmatrix}
x\\
y\\
1
\end{bmatrix}
\]

アフィン変換（回転移動）

Q31-Q40

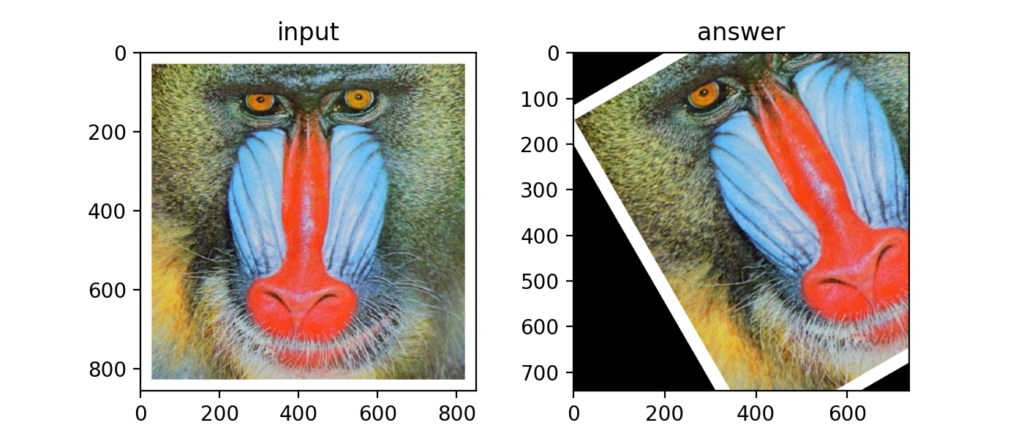
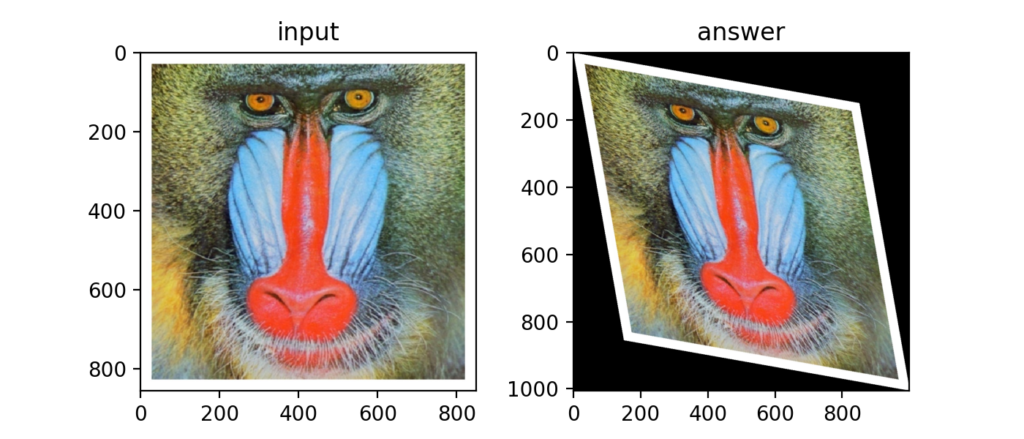
Q31：アフィン変換(スキュー)

以下のようなねじり変形の事をスキューと呼びます。
式はXのせん断方向、Yのせん断方向をそれぞれ使います。

\[
\begin{bmatrix}
{x}'\\
{y}'\\
1\end{bmatrix}=
\begin{bmatrix}
1 &\frac{dx}{h} &tx \\
0 &1 &ty \\
0 &0 &1
\end{bmatrix}
\begin{bmatrix}
x\\
y\\
1
\end{bmatrix},
\begin{bmatrix}
{x}'\\
{y}'\\
1\end{bmatrix}=
\begin{bmatrix}
1 &0 &tx \\
\frac{dy}{w} &1 &ty \\
0 &0 &1
\end{bmatrix}
\begin{bmatrix}
x\\
y\\
1
\end{bmatrix}
\]

アフィン変換（スキュー）

Q32：フーリエ変換

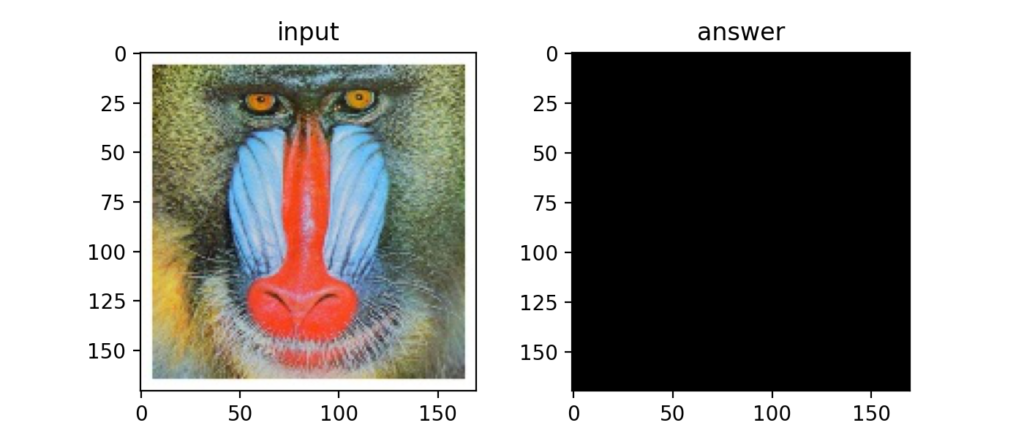
画像に対して2次元のフーリエ変換（次式）をかけると、2次元のスペクトルを得る事が出来ます。

\[ G(k,l)=\frac{1}{HW}\sum_{y=0}^{H-1}\sum_{x=0}^{W-1}I(x,y)e^{-2\pi j(\frac{kx}{W}+\frac{ly}{H})}\]

結果は以下。うーん、非常に小さい値は入っているが真っ黒ですね。

2次元フーリエ変換

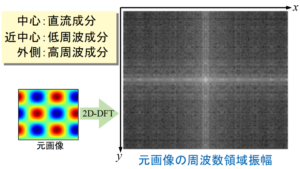
「Pythonで2Dフーリエ変換!画像フィルタリングをする方法」ではnumpyのfft.fft2を使って2Dのフーリエ変換をしましたが、以下のような絵になりました。今回の場合とどこが違うかを調べるのは結構時間がかかりそうですね。実用上はライブラリを使うのが便利ですが、どんな式を使っているかを学べたのはよかったです。

ちなみに逆変換は次式との事。

\[ I(x,y)=\frac{1}{HW}\sum_{l=0}^{H-1}\sum_{k=0}^{W-1}G(k,l)e^{2\pi j(\frac{kx}{W}+\frac{ly}{H})}\]

Q33：フーリエ変換(ローパスフィルタ)

画像に対してスペクトルを求めるフーリエ変換と、スペクトルを画像に戻すフーリエ逆変換を使うと画像データに対するフィルタリングが可能になります。

以下はローパスフィルタの例。高周波成分が除去されたので、若干ぼやけたような画像になりました。

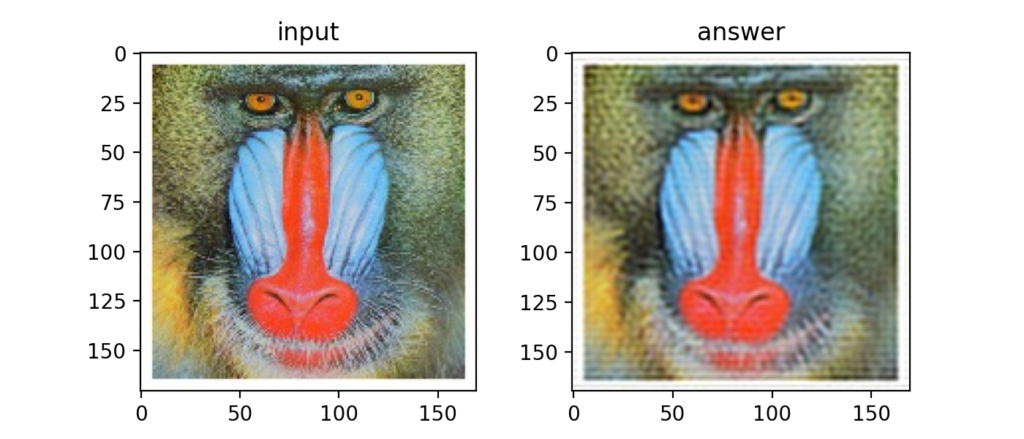
フーリエ変換（ローパスフィルタ）

Q34：フーリエ変換(ハイパスフィルタ)

次はハイパスフィルタの例。今度は急激な輝度変化をしている所だけを抽出しています。

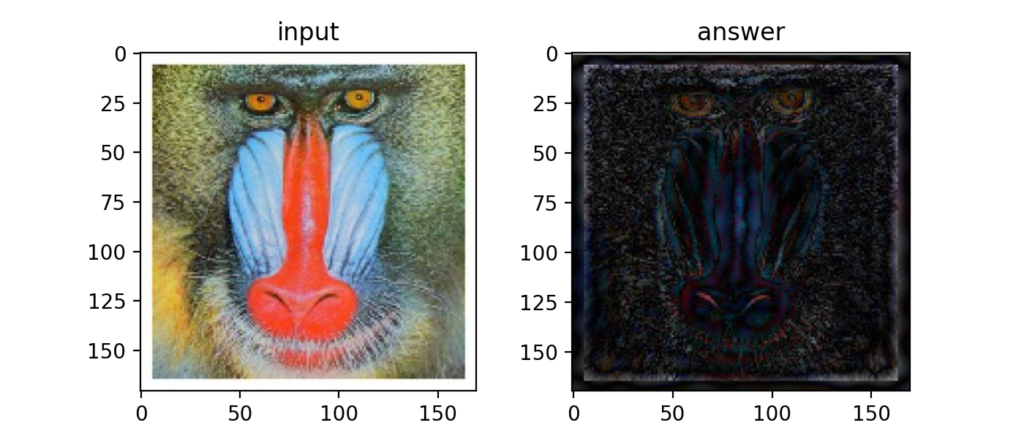
フーリエ変換（ハイパスフィルタ）

これは先ほど紹介した記事内の画像ですが、2次元のフーリエ変換を使ったフィルタリングは以下のイメージです。

DFTのフィルタリング

Q35：フーリエ変換(バンドパスフィルタ)

ローパスとハイパスが出来るという事は、もちろんバンドパスフィルタも可能。

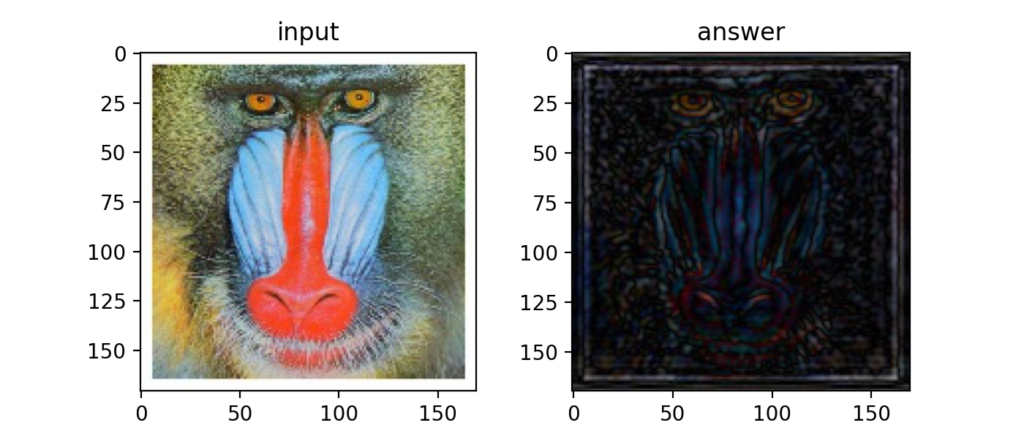
フーリエ変換（バンドパスフィルタ）

Q36：離散コサイン変換

離散コサイン変換（DCT：Discrete Cosine Transformation)とは画像を縦横N分割にしてJPEGの圧縮等に使われる。

ここ（外部サイト様：DCT(離散コサイン変換)によるデータ圧縮）DCTを行う事で画像そのものより軽量なDCT係数を取得し、画像として表示させるためにはDCT係数をIDCT（逆離散コサイン変換）で復元する…という感覚でしょうか？難しい。

一応写経してみたけど、できてるっぽい。

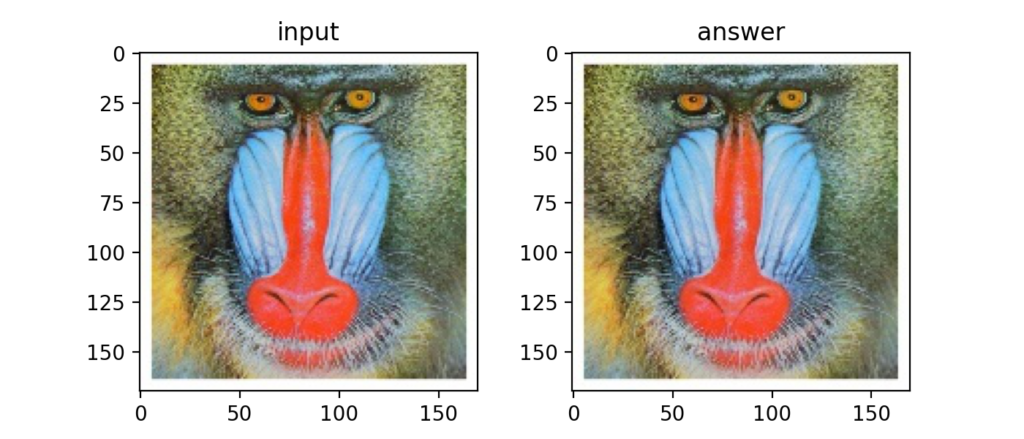
離散コサイン変換と逆離散コサイン逆変換

Q37：PSNR

PSNR(Peak Signal to Noise Ratio)は信号対ノイズ比。画像の劣化を評価する指標として使われるとの事。

\[ PSNR=10\log_{10}\frac{v_{max}^{2}}{MSE}\\ MSE=\frac{1}{HW}\sum_{y=0}^{H-1}\sum_{x=0}^{W-1}\left \{ (I_{1}(x,y)-I_{2}(x,y)) \right \}^{2}\\ Bitrate=8\frac{K^{2}}{8^{2}} \]

Q38：DCT+量子化

DCT係数を予め決定されたある区分毎に大まかに丸め込む事で量子化を行う事でデータ量を削減する事が出来る。

この区分、つまり量子化テーブルはjpeg団体という組織の仕様書で決められているとの事（そんな団体あったんか）。

Q39：YCbCr表色系のJPEG圧縮

Jpeg画像はYCbCrで色を保存しているとの事。
この分野は知らない事だらけなのですが、こちらのサイト様（外部サイト：JPEG の YCbCr について）がわかりやすかったです。

RGBとYCbCrの相互変換式は以下。

\[ Y=0.299R+0.5870G+0.114B\\ Cb=-0.1687R-0.3313G+0.5B+128\\ Cr=0.5R-0.4187G-0.0813B+128 \]
\[ R=Y+1.402(Cr-128)\\ G=Y-0.3441(Cb-128)-0.7139(Cr-128)\\ B=Y+1.7718(Cb-128) \]
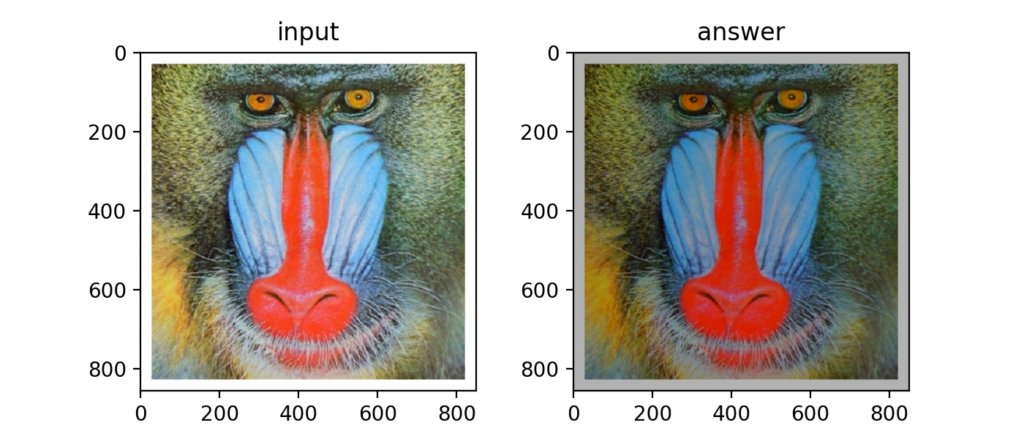
RGB→YCbCr変換

Q40：YCbCr+DCT+量子化

上記までの手法を組み合わせると、
①RGBをYCbCrに変換する。
②YCbCrをDCTする。
③DCTしたものを量子化テーブルで量子化する。
④量子化したものをIDCTする。
⑤IDCTしたYCbCrをRGBに変換する。
…という事ができ、画像の容量が削減される効果があるとの事。

Q41-Q50

Q41：Cannyエッジ検出 ①：エッジ強度と角度

Cannyエッジ検出というエッジ検出処理を行うために、Gaussian filterとSobel filterを使ってエッジ強度とエッジ角度を求めた結果が下図。

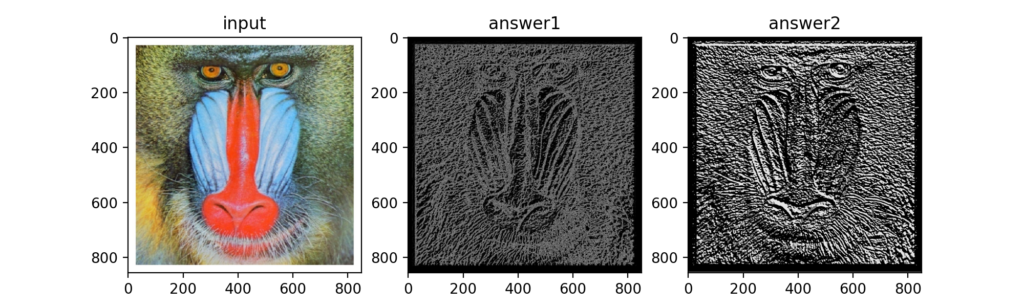
Cannyエッジ検出：エッジ強度とエッジ角度

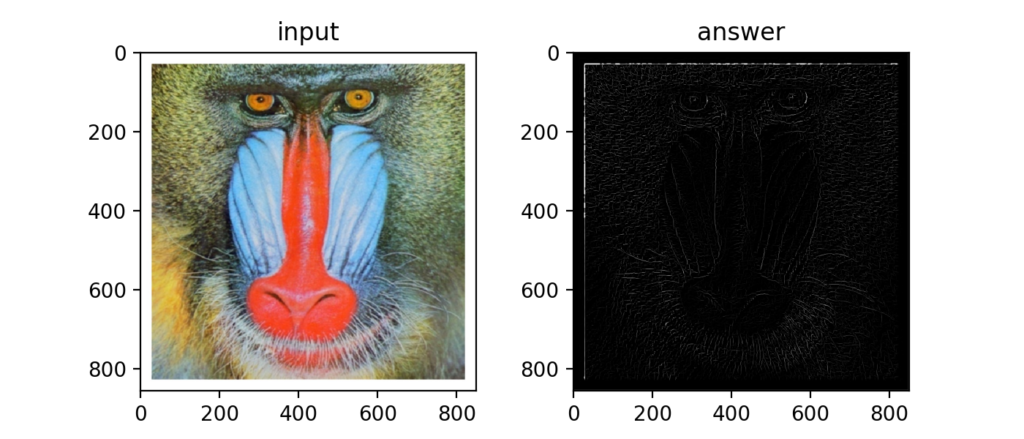
Q42：Cannyエッジ検出 ②：細線化

最大値で無い値を抑制するというNon-Maximum Suppression(NMS)を使うと以下のように線が細くなります。

Cannyエッジ検出：細線化

Non-Maximum Suppressionは何も画像処理に限ったアルゴリズムではないようです。

外部サイト様：「Non-Maximum Suppressionを世界一わかりやすく解説する」

Q43：Cannyエッジ検出 ③：ヒステリシス閾値処理

最後にLowとHighの二つの閾値を使って二値化するのがヒステリシス閾値処理。ここまでがCannyエッジ検出の内容。

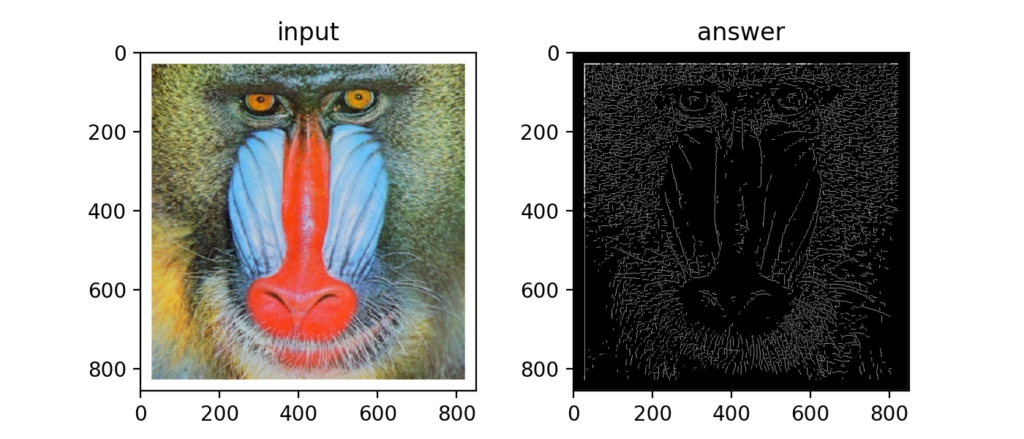
Cannyエッジ検出：ヒステリシス閾値処理

Q44：Hough変換①

Hough変換は直線を検出するために行います。手順はまずエッジ検出（ここでは先ほどのCannyエッジ検出の結果を使用）を行い、その結果についてHough変換(次式)を行います。検出されたエッジ部分の直交座標を極座標に変換しているとのこと。

\[ \rho = x \cos(t) + y \sin (t) \]

さらにこの後ボーディング（投票）という作業を行い、表を描画する（詳しく説明できないのでGitHubを参照下さい）。

下図は建物の画像をHough変換してボーディングした図。

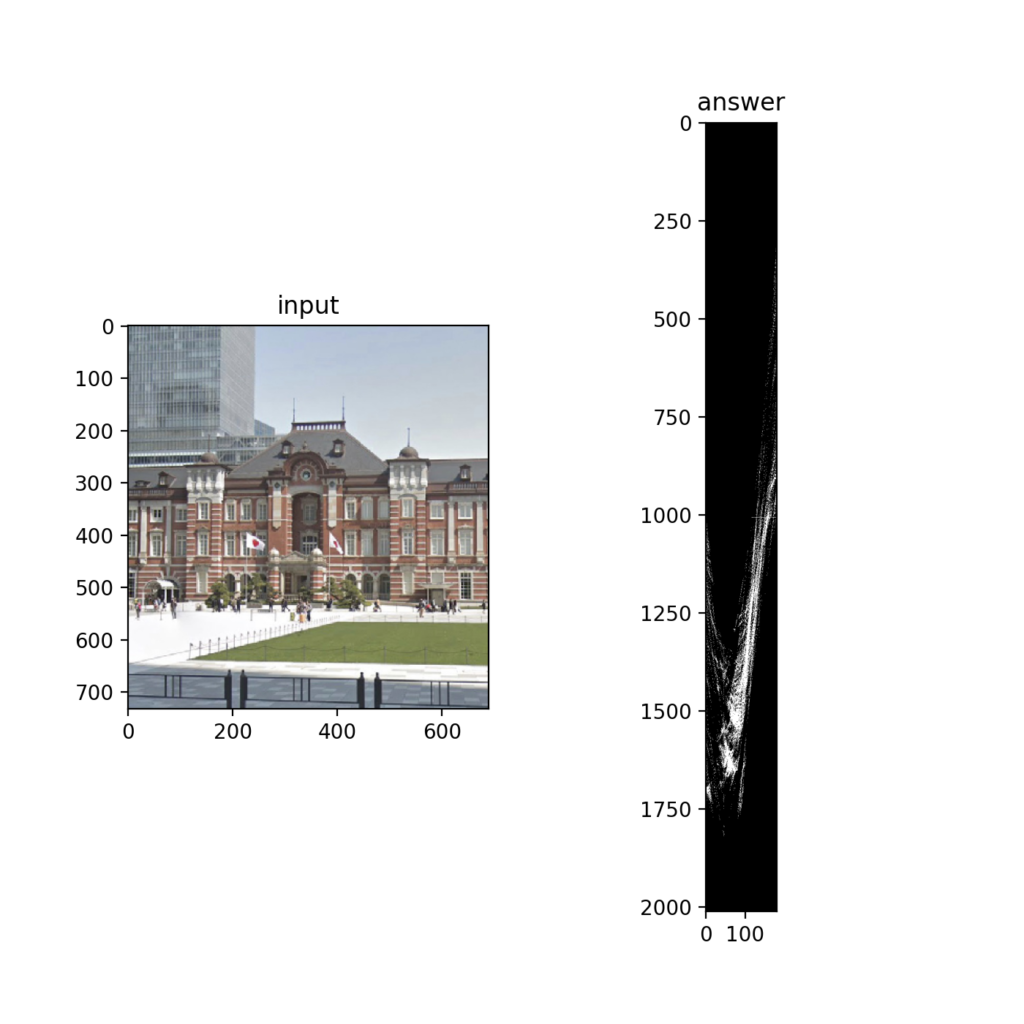
Hough変換1

Q45：Hough変換②

さらにNMS（Non-Maximum Suppression）を行い極大値を抽出する。

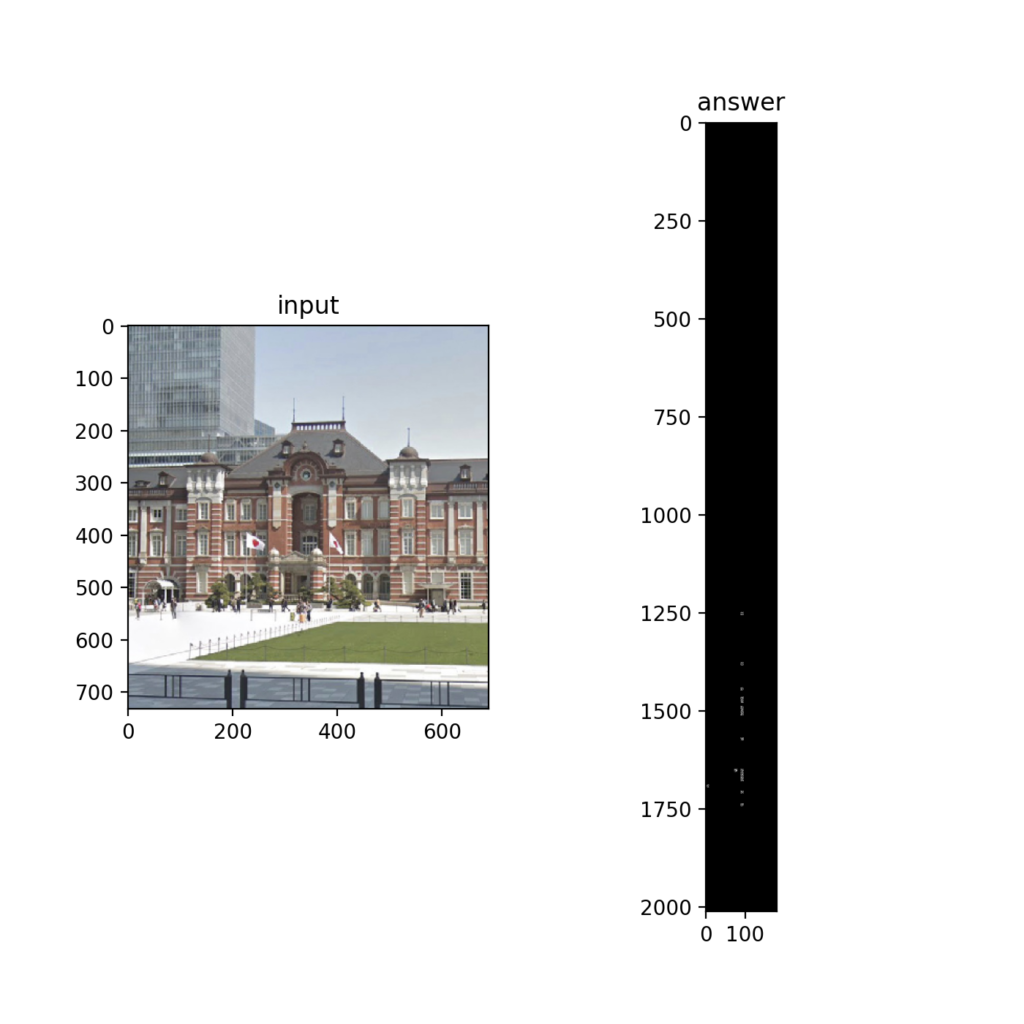
Hough変換2

Q46：Hough変換③

最後に逆Hough変換を次式で行う。

\[ y=-\frac{\cos(t)}{\sin(t)} x + \frac{r}{\sin(t)}\\ x=-\frac{\sin(t)}{\cos(t)} y + \frac{r}{\cos(t)} \]
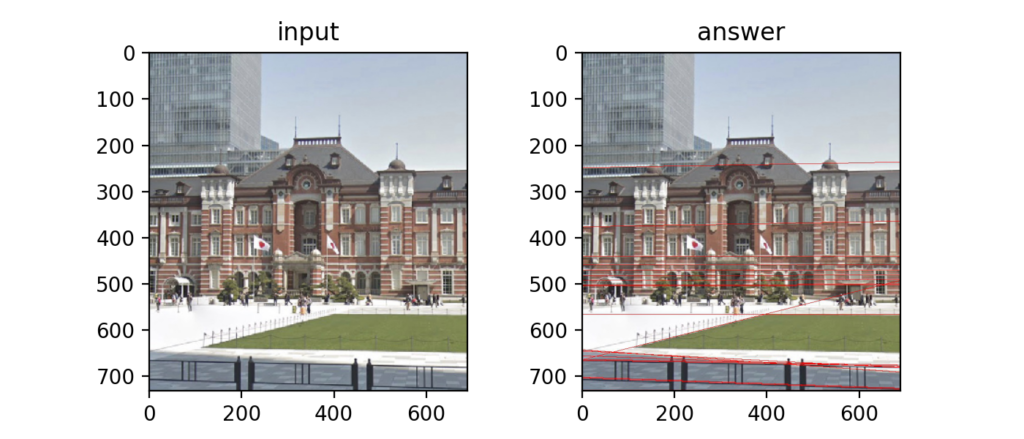
Hough変換3

Q47：モルフォロジー処理(膨張)

二値化（ここでは大津の二値化）した輝度255の画素を膨張させたり収縮させたりする処理をモルフォロジー処理という。以下は白い所を膨張(Dilation)させた例。

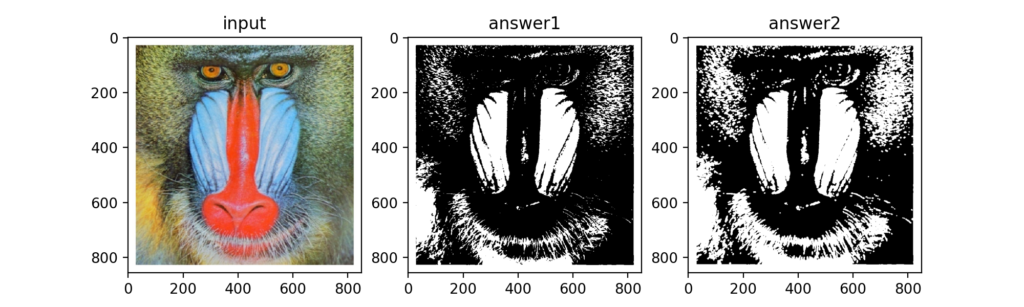
モルフォロジー処理（膨張）

Q48：モルフォロジー処理(収縮)

次は収縮(Erosion)。

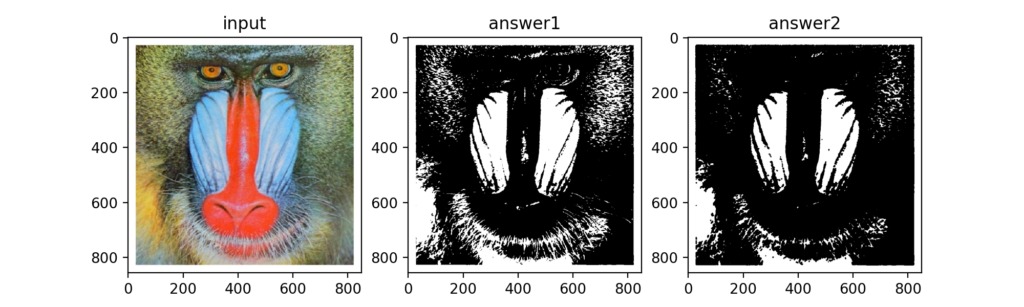
モルフォロジー処理（収縮）

Q49：オープニング処理

モルフォロジー処理の収縮をN回行って小さい画素を消した後に、膨張をN回行って残っている画素だけを元に戻すオープニング処理をする事で余分な画素を削除する事ができる。

Q50：クロージング処理

オープニング処理とは逆に、膨張をN回行った後に収縮をN回行うクロージング処理をする事で、微小に途切れている所を結合する事ができる。

Q51-Q60

Q51：モルフォロジー勾配

モルフォロジー勾配はモルフォロジー処理の膨張と収縮の差をとる事で境界を検出する処理の事。

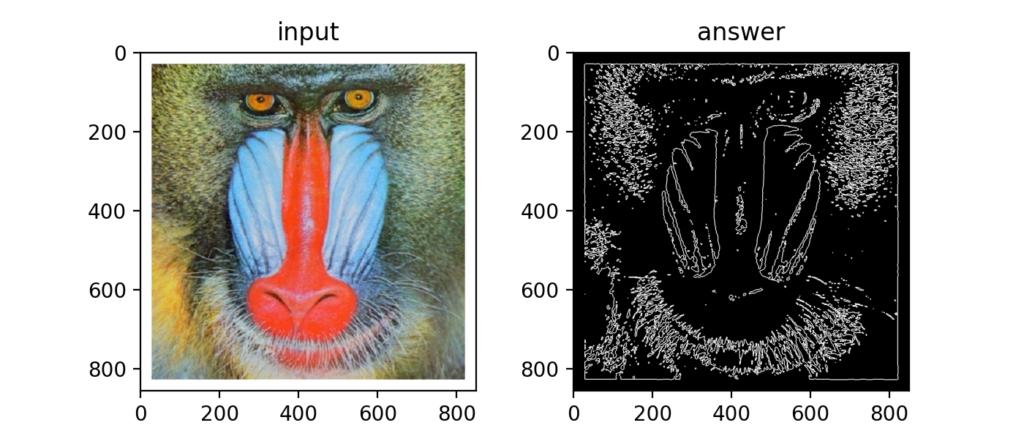
モルフォロジー勾配

Q52：トップハット変換

トップハット変換は大津の二値化からオープニング処理後の画像を引いたもの。細かいノイズ成分を検出する事ができる。

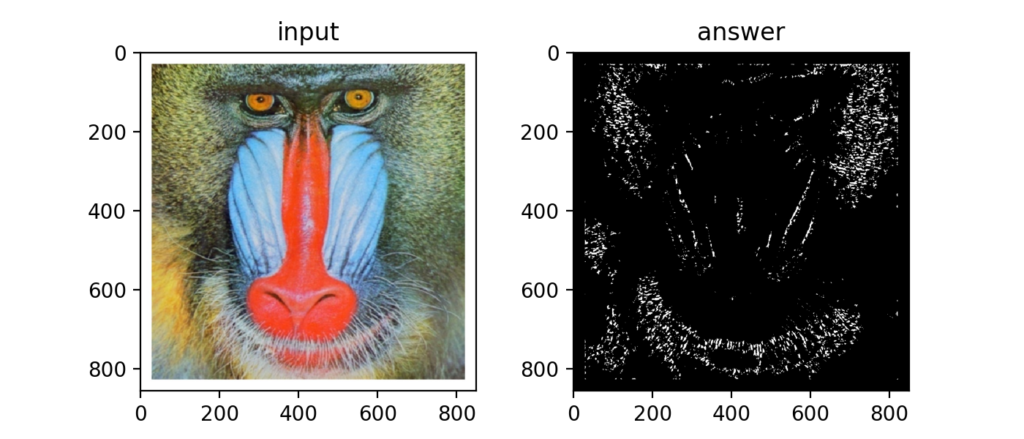
トップハット変換

Q53：ブラックハット変換

大津の二値化からクロージング処理の結果を引いたらブラックハット変換になる。

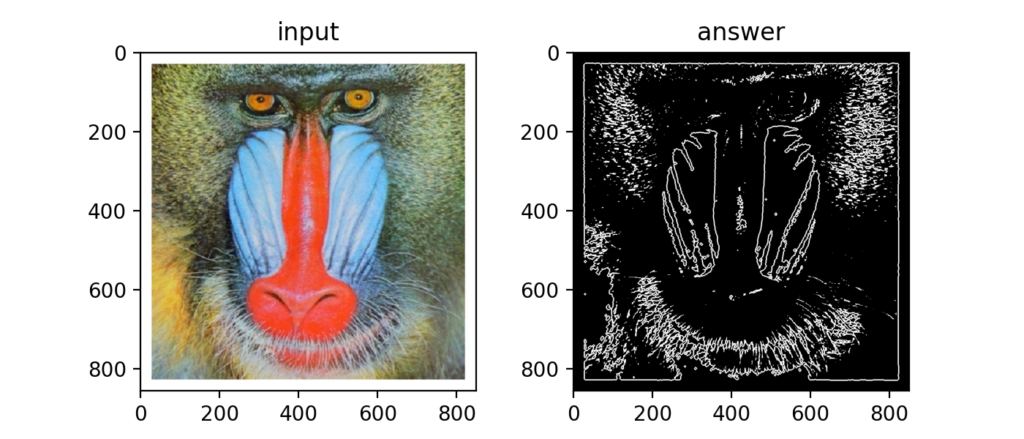
Q54：テンプレートマッチング(SSD)

元画像\(I\)の中で、テンプレート画像\(T\)と最も近い部分を探す事をテンプレートマッチングと呼びます。ここで、その中でも最も基本的なSSD(Sum of Squared Difference)が次式の最小値となる\(d_{x}\)と\(d_{y}\)を求める事です。

\[ SSD(d_{x}, d_{y})=\sum_{x=0}^{W-1}\sum_{y=0}^{H-1}\left \{ (I(x+d_{x},y+d{y})-T(x,y)) \right \}^{2} \]

以下がSSDで検出した範囲をcv2.rectangle()で囲んだ結果。

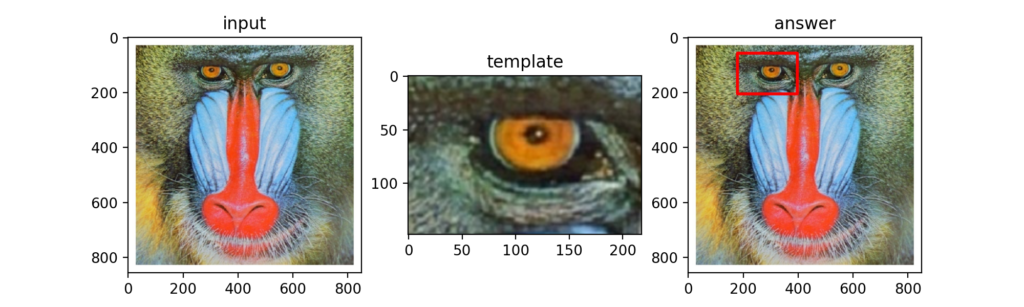
テンプレートマッチング（SSD）

Q55：テンプレートマッチング(SAD)

SSDと似ていますが、SAD(Sum of Absolute Difference)と次式のように絶対値をとって式が最小となる位置を探すテンプレートマッチング手法もあります。

\[ SAD(d_{x}, d_{y})=\sum_{x=0}^{W-1}\sum_{y=0}^{H-1}\left |(x+d_{x},y+d{y})-T(x,y)\right | \]

Q56：テンプレートマッチング(NCC)

NCC(Normalized Cross Correlation)は正規化相互相関の事で、類似度を評価するテンプレートマッチング手法です。次式で表し、値が-1から1までをとり、1に近いほど相関があるという指標。NCCはSSDやSADに比べ照明の変化に強いという特性を持ちます。

\[ NCC(d_{x},d_{y})=\frac{\sum_{x=0}^{W-1}\sum_{y=0}^{H-1}\left [ I(x+d_{x},y+d_{y})T(x,y) \right ]}{\sqrt{\sum_{x=0}^{W-1}\sum_{y=0}^{H-1}\left [ I(x+d_{x},y+d_{y})\right ]^{2}}\sqrt{\sum_{x=0}^{W-1}\sum_{y=0}^{H-1}\left [ T(x,y)\right ]^{2}}} \]

Q57：テンプレートマッチング(ZNCC)

NCCの各画像平均との差をとる事で、ZNCC(Zero means Normalized Cross Correlation)になります。

\[ ZNCC(d_{x},d_{y})=\frac{\sum_{x=0}^{W-1}\sum_{y=0}^{H-1}\left [ (I(x+d_{x},y+d_{y}-\mu_{I}))(T(x,y)-\mu_{T}) \right ]}{\sqrt{\sum_{x=0}^{W-1}\sum_{y=0}^{H-1}\left [ I(x+d_{x},y+d_{y})-\mu_{I}\right ]^{2}}\sqrt{\sum_{x=0}^{W-1}\sum_{y=0}^{H-1}\left [ T(x,y)-\mu_{T}\right ]^{2}}} \]

Q58：ラベリング：4近傍

白黒画像に対して、隣り合うピクセルでラベルを当てはめていくラベリングがある。最も簡単なラベリングは着目画素の4方向を見る4近傍法。

ラベリングの際にはルックアップテーブルを使うのが特徴。

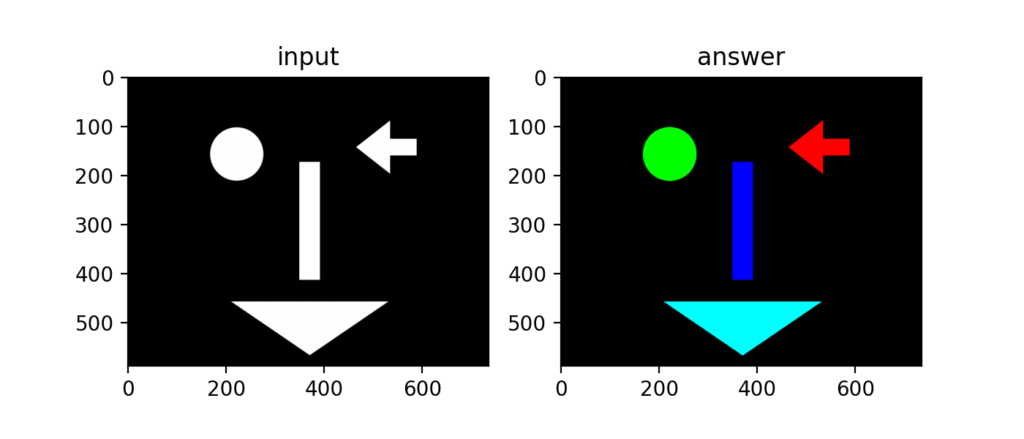
ラベリング

Q59：ラベリング：8近傍

4近傍の他に、8近傍法のラベリングも可能。

8方向見る事で、斜めの画素の接続まで考慮する事ができるようになる。

Q60：アルファブレンド

2つの画像のアルファチャンネルの値を変更して合成する事をアルファブレンドと呼ぶ。

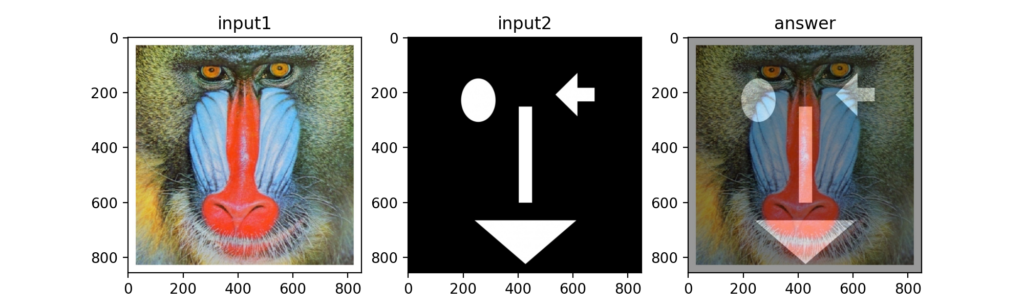
アルファブレンド

Q61-Q70

Q61：連結数（4連結）

ある画素x_{0}に着目し、各位置を以下のように定義する。

\[ \begin{bmatrix} x_{4}(x-1,y-1) &x_{3}(x,y-1) &x_{2}(x+1,y-1) \\ x_{5}(x-1,y) &x_{0}(x,y) &x_{1}(x+1,y) \\ x_{6}(x-1,y+1) & x8(x,y+1) &x_{8}(x+1,y+1) \end{bmatrix} \]

4近傍を使って連結数は次式で計算する。

\[ S = (x_{1} - x_{1} x_{2} x_{3}) + (x_{3} - x_{3} x_{4} x_{5}) + (x_{5} - x_{5} x_{6} x_{7}) + (x_{7} - x_{7} x_{8} x_{1}) \]

Q62：連結数（8連結）

先ほどの4連結においてxの0と1を入れ替えた値を使うと8連結の連結数を計算可能となる。

Q63：細線化処理

細線化処理（幅を1にする）を使うと下図のように文字を細くしたりできる。

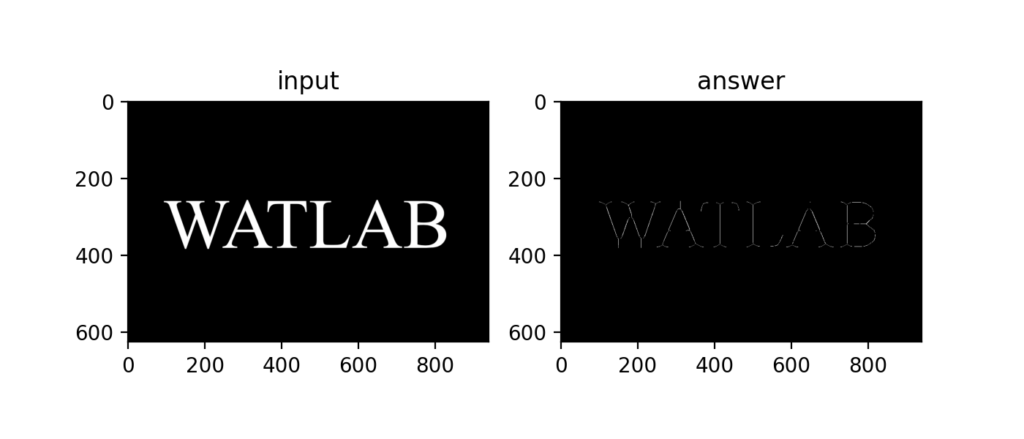
細線化処理

Q64：ヒルディッチの細線化処理

8連結数を使うヒルディッチの細線化処理。

先ほどよりも綺麗に文字を再現する事が出来ました。

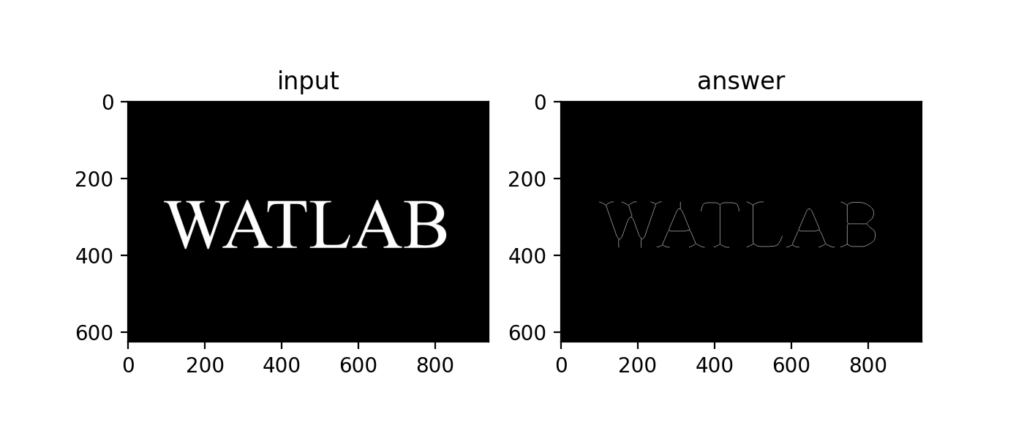
ヒルディッチの細線化処理

Q65：Zhang-Suenの細線化処理

複数STEPと反復処理を行うZhang-Suenの細線化が以下。

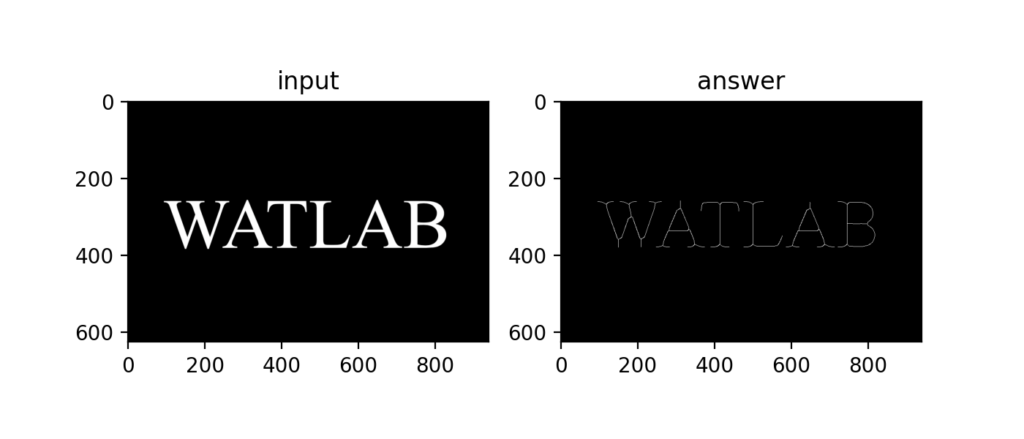
Q66：HOG①：勾配強度・勾配角度

グレースケール画像に対しx,yの輝度勾配\(gx, gy\)を求め、

\[ g_{x} = I(x+1, y) - I(x-1, y)\\ g_{y} = I(x, y+1) - I(x, y-1)\\ \]

勾配強度と勾配角度を求めるのがHOG(Histogram of Oriented Gradients)のSTEP1。

\[ mag = \sqrt{g_{x}^{2} + g_{y}^{2}}\\ ang = \arctan(\frac{g_{y}}{g_{x}}) \]
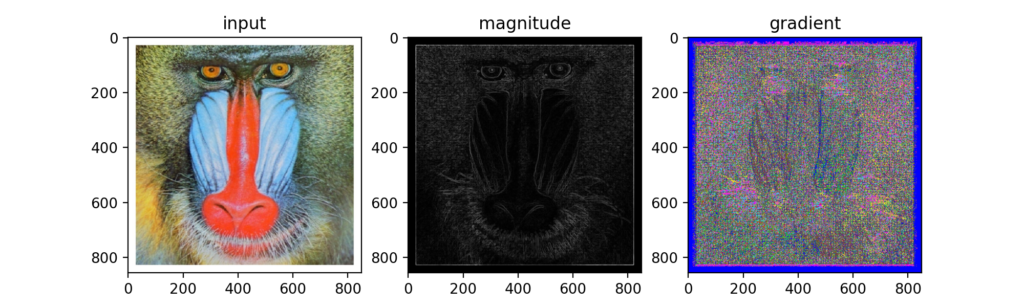
HOG：勾配強度と勾配角度

Q67：HOG②：勾配ヒストグラム

画像をN×N領域に分割し、量子化した勾配角度のヒストグラムをそれぞれ求めるのがHOGのSTEP2。

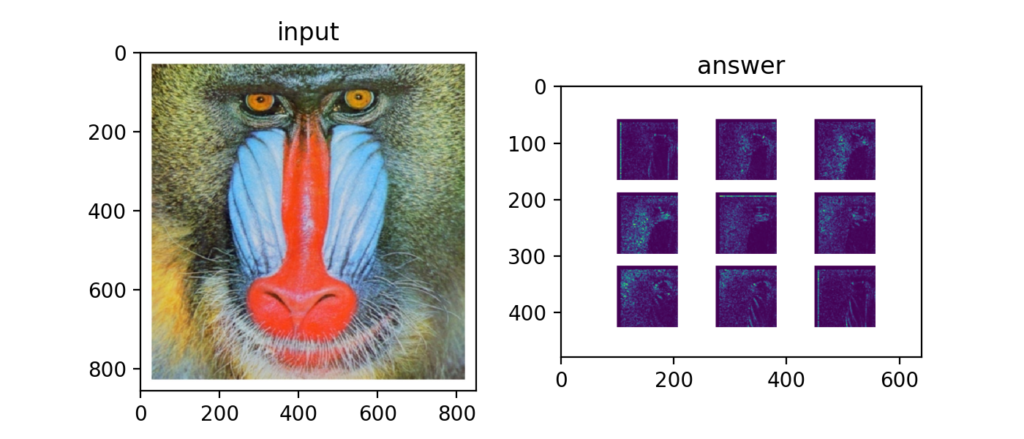
HOG：勾配ヒストグラム

Q68：HOG③：ヒストグラム正規化

さらにブロック毎にヒストグラムを正規化するとHOG特徴量と呼ばれる量が計算された事になる。

\[ h(t) = \frac{h(t)}{\sqrt{\sum{h(t)} + \epsilon}} \]
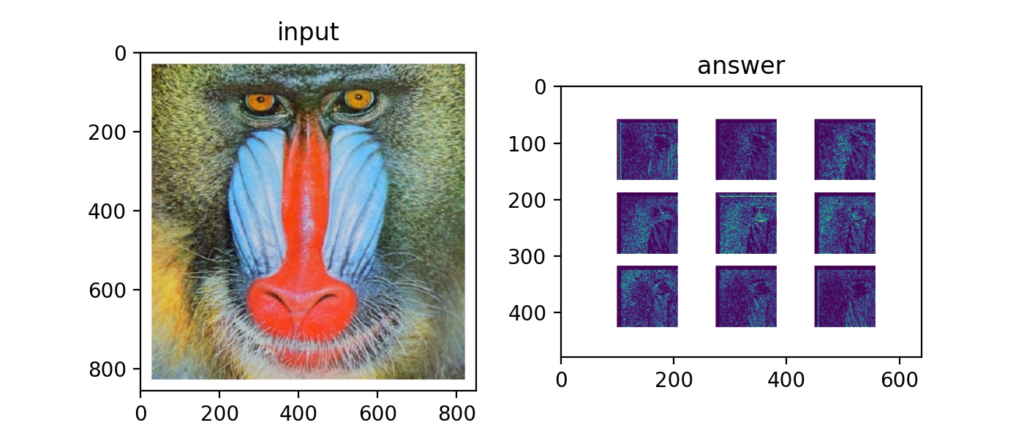
HOG：ヒストグラム正規化

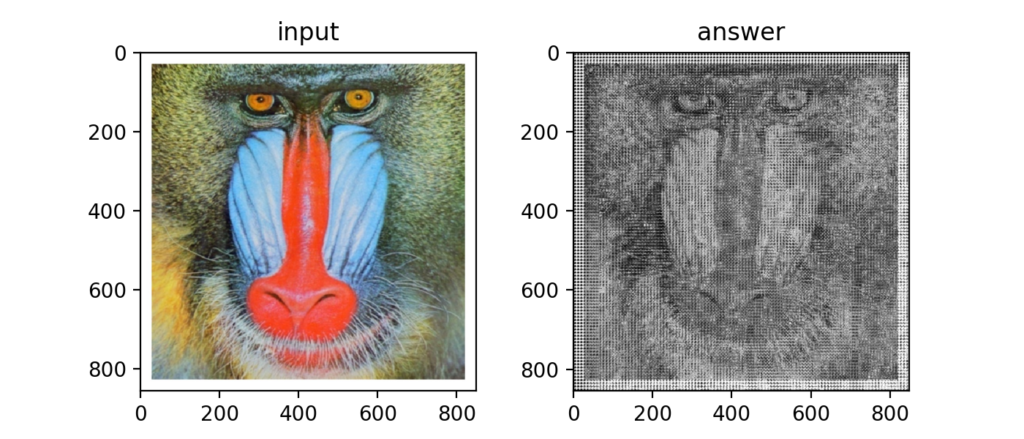
Q69：HOG④：HOG特徴量の描画

HOG特徴量を元画像に重ねて描画するとわかりやすくなる。CNNが台頭する前はこういった特徴量を使って画像の分類をしていたのだとか。

HOG：特徴量の描画

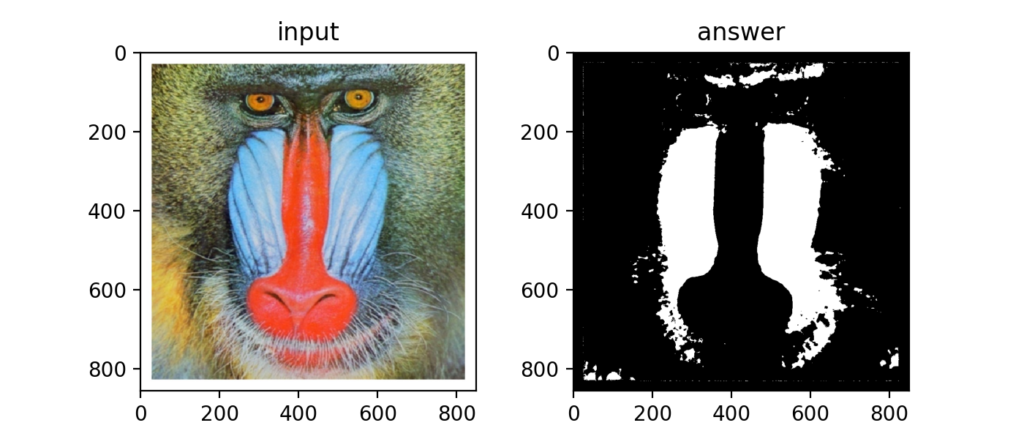
Q70：カラートラッキング

RGBではなくHSVスケールを使えば「青っぽい色」といったカラートラッキングが可能になる。

HSVによるカラートラッキング

Q71-Q80

Q71：マスキング

カラートラッキングした部分を元画像に対して黒くする事をマスキングと呼ぶ。

カラートラッキングで得られた255の画素を1として、それを反転した0との積をとる事で実現できる。

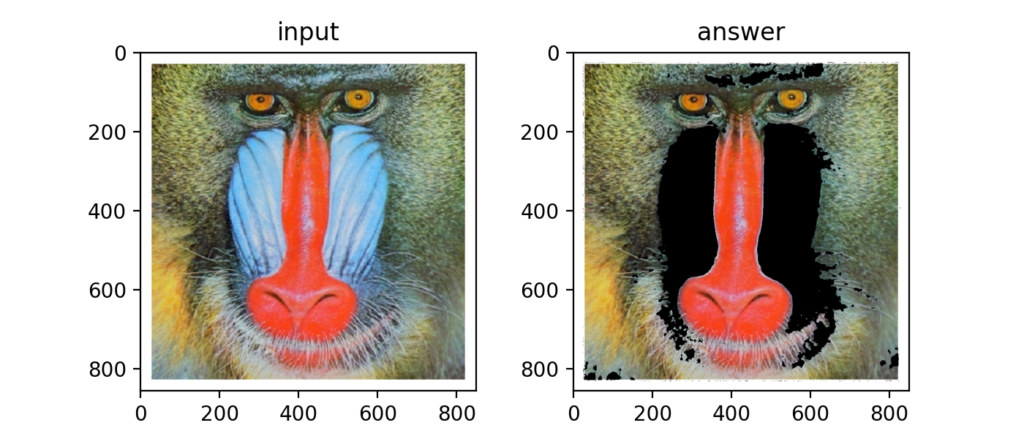
マスキング

Q72：マスキング：カラートラキング＋モルフォロジー

先ほどの結果にクロージング処理とオープニング処理というモルフォロジー処理を行い、マスキングの輪郭を綺麗にする事ができる。

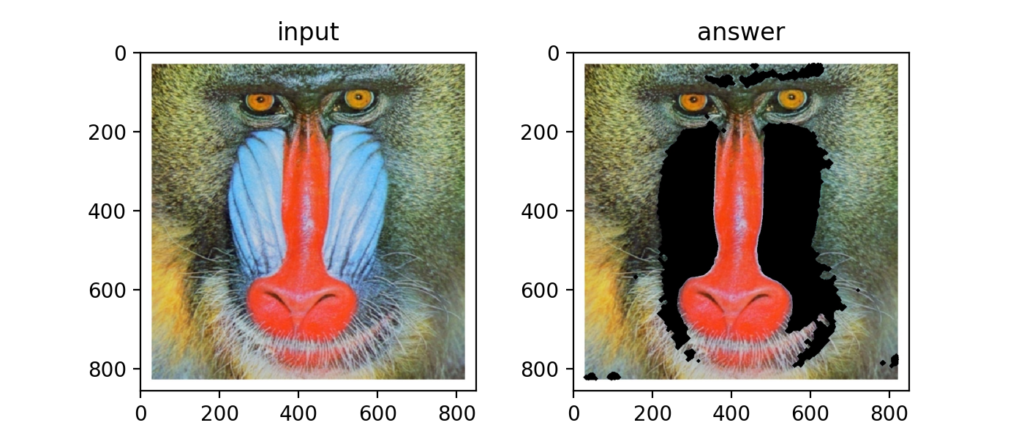
マスキング：カラートラキング＋モルフォロジー

Q73：縮小と拡大(高周波成分のカット）

画像を単に縮小してから拡大する事でぼやけた画像、すなわち高周波成分を除去した画像を取得する事ができる。

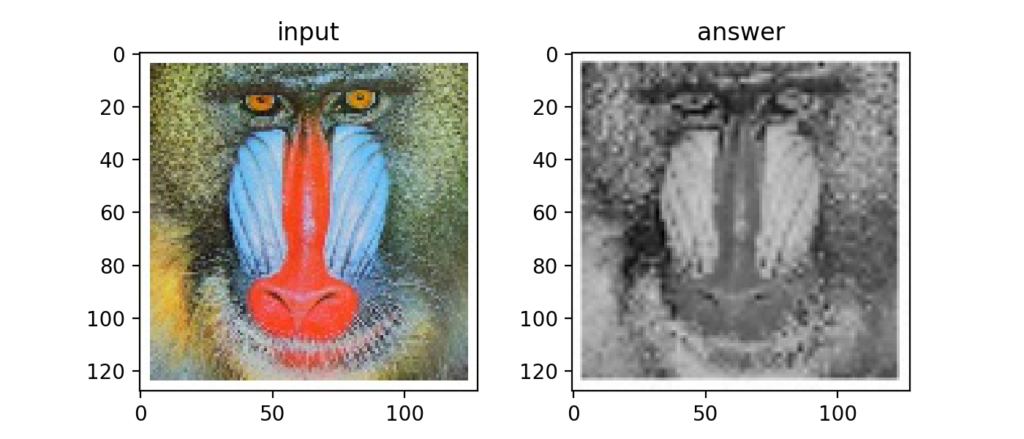
拡大と縮小

Q74：ピラミッド差分による高周波成分の抽出

先ほど求めた画像と元画像との差をとるとエッジを表現する事ができる。

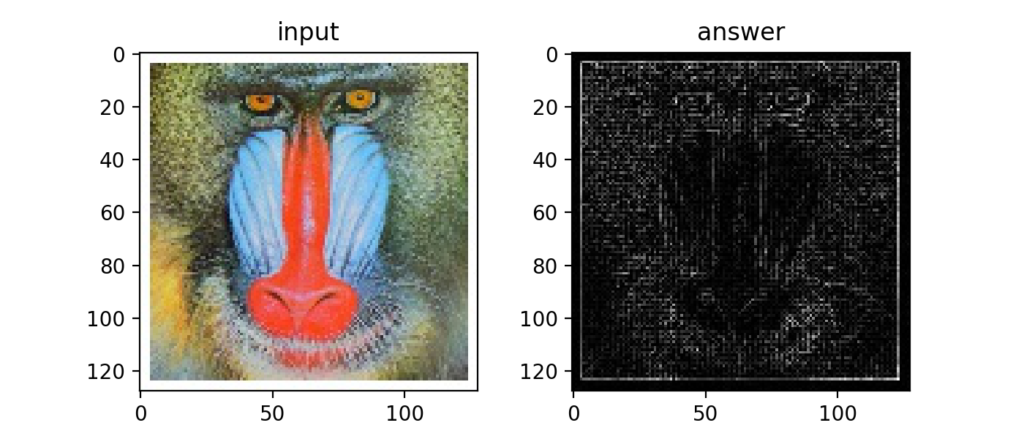
Q75：ガウシアンピラミッド

元画像を1/2, 1/4, 1/8, 1/16, 1/32…と小さくして重ねる事をガウシアンピラミッドと呼ぶ。ディープラーニングでも使われている考え方との事。

ガウシアンピラミッド

Q76：顕著性マップ（サリエンシーマップ）

ガウシアンピラミッドを用いて顕著性マップ（サリエンシーマップ）を作成する事ができる。この顕著性マップは当ブログでも「Pythonでサリエンシーマップを作成！人の視線の行き場を数値化」という記事で扱いましたが、作り方は今回初めてしりました。

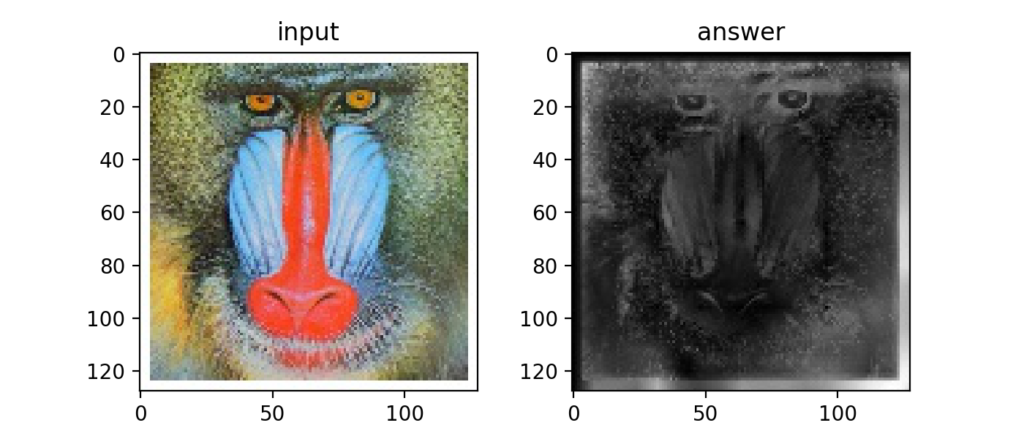
Q77：ガボールフィルタ

画像の特定方向のみのエッジを検出する事に使うガボールフィルタ。

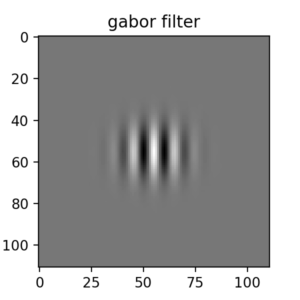
ガボールフィルタ

Q78：ガボールフィルタの回転

任意方向のエッジを検出するために、ガボールフィルタは回転させて使用する。

Q79：ガボールフィルタによるエッジ抽出

回転させたガボールフィルタを画像に対して適用する事で角度毎のエッジを抽出する事ができる。

ガボールフィルタによるエッジ抽出

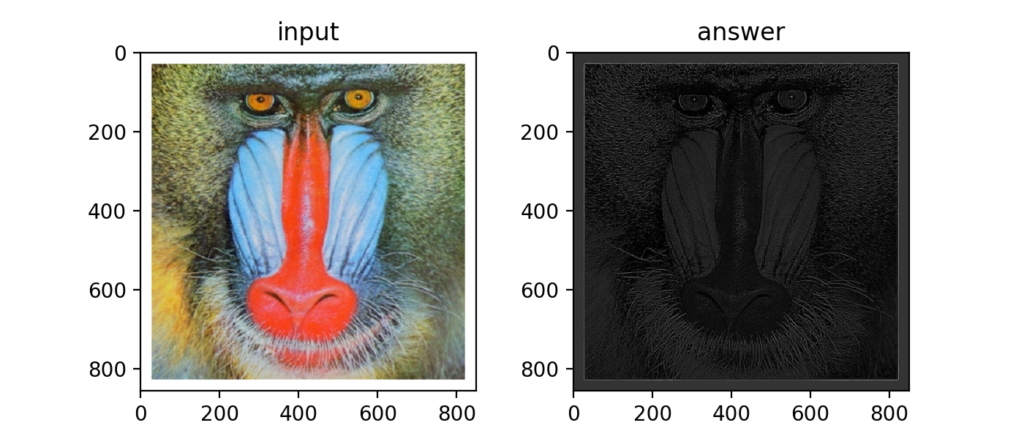
Q80：ガボールフィルタによる特徴抽出

先ほどの4毎のガボールフィルタ後のエッジを足し合わせると下図のように画像の特徴を抽出する事ができる。ディープラーニングではこれらを求めるパラメータを学習する。

ガボールフィルタによる特徴抽出

Q81-Q90

Q81：Hessianのコーナー検出

Hessianという計算手法はコーナー検出で使われる。この計算はガウス曲率\(K\)を用いる。

\[ K=\frac{\det \rm{H}}{(1+I_{x}^{2}+I_{y}^{2})^{2}} \]

また、\(\rm H\)はヘッセ行列とも呼ばれ、以下で表す。
※\(I_{xx}\)等は2次微分を表す。

\[ \rm H＝\begin{bmatrix} I_{xx} &I_{xy} \\ I_{xy} &I_{yy} \end{bmatrix} \]

\(\rm H\)の行列式は次式に示す。

\[ \det \rm H=I_{xx}+I_{yy}-I_{xy}^{2} \]

Q82：Harrisのコーナー検出 ①：Sobel + Gaussian

上記Hessianを用いてHarrisのコーナー検出を行っていく。
Harrisのコーナー検出はグレースケール化した画像に対してSobelフィルタをかけてHessian行列を求める。

さらに、求めたHessian行列の各2次微分の変数\(I_{xx}, I_{yy}, I_{xy}\)にガウシアンフィルタをかける。

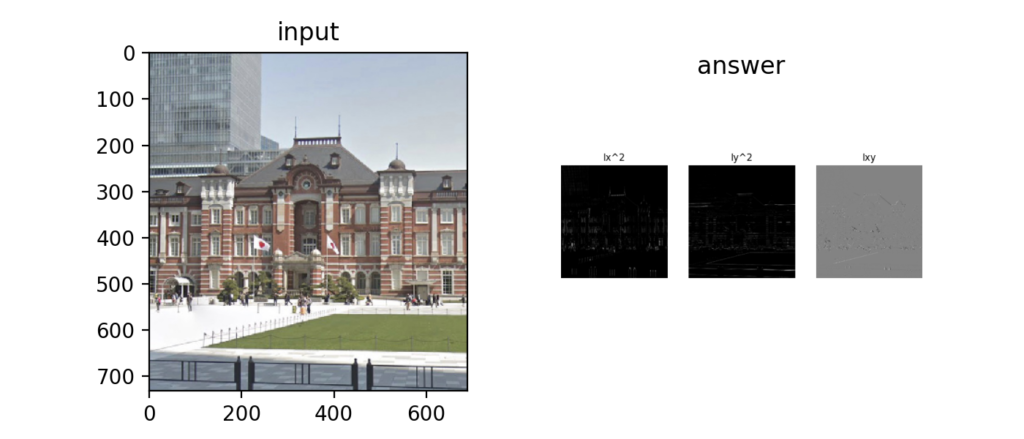
Harrisのコーナー検出：Hessian+Gaussian

Q83：Harrisのコーナー検出 ②：コーナー検出

次に、\(R = \det \rm H - k (trace(\rm H))^{2}\)をピクセル毎に計算し、\(R \geq max(R) \times th\)となる点を探す。

Harrisのコーナー検出

一応コーナーの一部が検出されてるっぽい。どうやらガウシアンフィルタのカーネル、偏差、閾値や\(k\)の値がハイパーパラメータのようで、これらの値で精度が変わるらしい。

Harrisのコーナー検出:Up

Q84-Q87：簡単な画像認識 ①：減色化 + ヒストグラム→クラス判別→評価→kNN法

ここからはサンプルの画像がオリジナルで揃えられなかったので、単純にメモだけ記録していきます。

CNNは画像の特徴量抽出も含めて学習していく手法ですが、CNNが台頭する前は画像の特徴量をプログラマが設計し、それを基に画像の分類等を行う必要があった。

その中には、減色化した画像のヒストグラムを特徴量とするアルゴリズムもある。色が近いと同じクラスに分類されるというもの。

精度＝正解した数/テストした画像の総数

色合いの近さでクラス分類するk-NN法がある。

k-NN法は当ブログでも「Python/sklearnのk近傍法!kNNで多クラス分類する」で書きましたが、画像処理でも使われるんですね。

Q88-Q90：k-means法

画像処理100本ノックがだんだんとAIっぽくなってきた！

k-means法は当ブログでは「Python/k-means法で教師なし学習!クラスタリング概要」という記事で1から実装したのでこちらは大丈夫そう。気になる方はこの記事をご覧下さい。

Q91-Q100

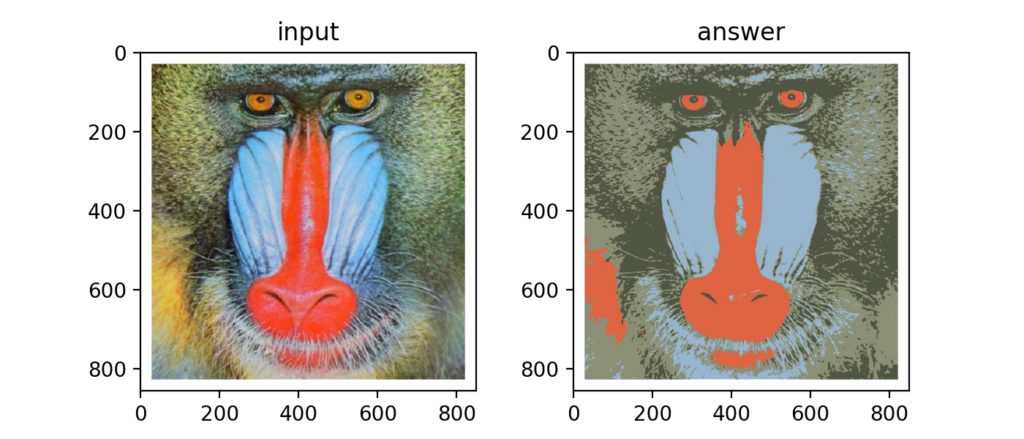
Q91：k-means法による減色処理

上記記事でも紹介しているk-means法は距離を使って教師無し学習であるクラスタリングを行う計算手法。色も距離を次式で定義する事ができる。

\[ d = \sqrt{(R-R')^{2} + (G-G')^{2} + (B-B')^{2}} \]
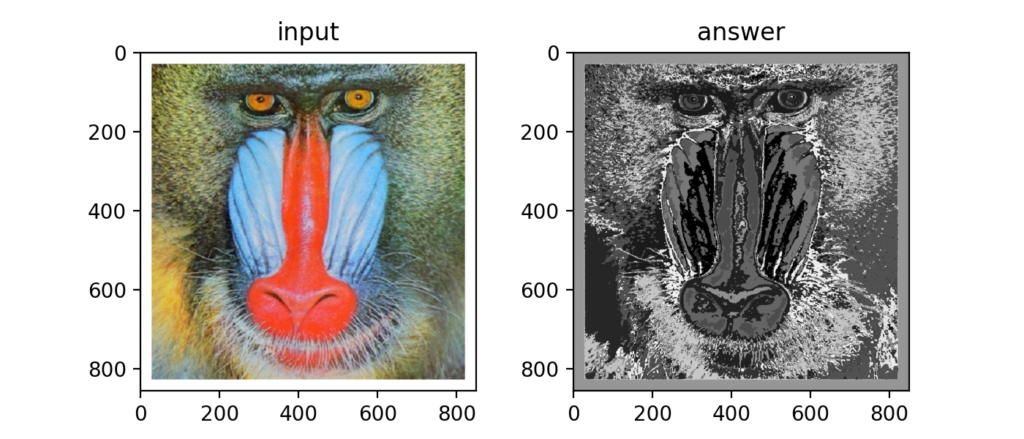
k-means法による減色処理

Q92：k-means法による減色処理

色を付けるとこんな感じ。これはk=5の例。

k-means法による減色2

Q93-Q100：ディープラーニングによる画像の分類

残りの問題はディープラーニングの実装による画像の分類ですが、自前の画像準備等にハードルがあるためここでは用語のまとめのみ行います。

（この辺はじっくりやらないと理解も難しい）

実はS級試験の数日前にこれを書いています…。

・正解：GT（Ground-Truth)
・IoU：Intersection over Union
　\(R_{1}\)：GTの領域
　\(R_{2}\)：切り抜いた領域
　\(Rol\)：GTと重なっている領域
　…とすると、
　\(IoU=\frac{\left | Rol \right |}{\left | R_{1}+R_{2}-Rol \right |}\)
　となる。

・ランダムクラッピング
　画像からランダムに矩形領域を切り抜いて学習データを作る事。

・バウンディングボックス
　物体を囲む矩形。画像の中で何を示しているかを表示する時に使う。

100本ノックを眺めた感想

今回AI実装検定S級を受験するにあたり、imori_imori(yoyoyo-yo)さんの「画像処理100本ノック」を"眺めて"みました。

"眺めて"というのは、まだ全て自力でやっていないからです。

検定のシラバスになっているから拝見したコンテンツですが、ここまで画像処理の分野で網羅的に手法が載っているコンテンツに出会えた事に感動しています！

正直甘くみていたため試験前なのに全く学習の進捗ないという状況。
（こりゃ今回は落ちたな…。）

でもこの「画像処理100本ノック」は検定が終わってからもじっくり、何度も確認して自分のスキルにできるようにしたいと思いました。

これをきちんと理解するには専門外の僕の場合は数ヶ月くらいかかりそうなので、AI実装検定S級を受験の方は余裕を持った学習を計画するのが良いと思います。

試験後追記：なんと受かっていました！難しかったけど。

AI実装検定S級に合格したので勉強方法と試験内容を振り返る

いや〜！これはしんどい！これから受ける検定はおそらく落ちたでしょう→受かってました！開き直って、ダメもとでコードレベルのカンペを作って試験に挑みます…！
Twitterでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています！

SNSでもご購読できます。

コメント

コメントを残す

*