機械学習にはコスト関数の極小値を探すために、様々な最適化手法が考案されています。ここでは学習が進むにつれ学習率が調整されていくAdaGradをPythonのnumpyで実装する方法を学びます。
こんにちは。wat(@watlablog)です。ここでは機械学習の最適化手法であるAdaGradを習得することを目標とします！
AdaGradの概要
勾配降下法派生手法のおさらい
機械学習はコスト関数(損失関数、誤差関数とも呼ぶ)を最小化するように各重みベクトルを更新していく学習スタイルをとるものがあります。
この時、最も簡単な更新式は勾配降下法と呼ばれる手法で、関数の勾配情報を使って山を下っていくように極小値を探していく特徴を持ちます。
関数の最小値問題や勾配降下法については「Pythonで1変数と2変数関数の勾配降下法を実装してみた」に詳細を記載しましたので、よかったらそちらの記事も読んでみて下さい。
単純な勾配降下法は学習率が終始一定で、緩やかな勾配にさしかかったらすぐに変化量が小さくなる等の融通の利かなさがありました。
「勾配降下法に慣性項を追加するMomentumをPythonで実装」で紹介したMomentumは更新式に慣性項を追加することでより滑らかな変化をするようになりました。
AdaGradの更新式
AdaGradも学習の進捗によって重みの更新量を変化させ、より最適解に辿り着きやすくするよう改善された手法(2011年にDuchiらにより提唱された)です。
AdaGradの更新式を式(1)と式(2)に示します。
$$\mathbf{h}_{i+1}=\mathbf{h}_{i}+ (\nabla f)^{2} (1)$$
$$\mathbf{x}_{i+1}=\mathbf{x}_{i}-\eta \frac{1}{\sqrt{\mathbf{h}_{i+1}}} (\nabla f) (2)$$
ここで、最終的な更新式は式(2)となりますが、式(1)の\(\mathbf{h}\)が学習率の後にかかり、平方根で分母に来ています。
\(\mathbf{h}\)は必ず増分するように更新されていくため、この式は学習が進捗していけば各重み毎に学習率が変化することを意味します。
AdaGradのAdaとは、Adaptive(適応的)から来ており、この各重みに適応して学習率が変化するというのが主な改善内容です。
AdaGradのメリットとデメリット
Momentumは慣性項と、加算の形で前の更新量の影響を現段階の更新量に反映していますが、学習率は一定のままです。
そして、Momentumは学習率\(\eta\)と慣性係数\(\alpha\)の2つのハイパーパラメータ(エンジニアが事前に調整すべきパラメータ)を持っており、調整が困難であるというデメリットがありました。
対しAdaGradは学習率\(\eta\)だけがハイパーパラメータなので(\(\mathbf{h}\)は勾配から自動的に定まるため)、調整はMomentumと比較すれば容易になります。
このように、学習の進捗によって学習率を適応的に変化させること、ハイパーパラメータが少ないということの2つがAdaGradの主なメリットです。
しかし、AdaGradは学習が進むにつれ、学習率が減少する方向にしか変化しないというのが最大のデメリットで、最適解に届かないで学習が終了してしまう可能性も大いにあります。
巷では「これを使っておけば大丈夫という最適化手法は無い！」と言われています。この辺の選択は本当に難しい所ですね！
Python/NumpyによるAdaGradの実装コード
全コード
以下に全コードを示します。今回も過去同様、これまでの最適化手法と挙動を比較していきます。勾配は理論値として式(3)を用意しました。
$$z=\frac{1}{4}x^{2}+y^{2} (3)$$
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 |
import numpy as np from matplotlib import pyplot as plt from mpl_toolkits.mplot3d import Axes3D # グラフプロット用基準関数 def f(x, y): z = (1/4) * x ** 2 + y ** 2 return z # 基準関数の微分 def df(x, y): dzdx = (1/2) * x dzdy = 2 * y dz = np.array([dzdx, dzdy]) return dz # 共通のパラメータ max_iteration = 50 # 最大反復回数 eta = 0.1 # 学習率 # GDのパラメータ x0_gd = -10 y0_gd = 10 x_gd = [x0_gd] y_gd = [y0_gd] # Momentumのパラメータ alpha = 0.5 x0_mom = -10 y0_mom = 10 x_mom = [x0_mom] y_mom = [y0_mom] pre_update = np.array([0, 0]) # AdaGradのパラメータ eta_adagrad = 2 # AdaGradの学習率 x0_adagrad = -10 y0_adagrad = 10 x_adagrad = [x0_adagrad] y_adagrad = [y0_adagrad] h0 = np.array([0, 0]) # 最大反復回数まで計算する for i in range(max_iteration): # GDの更新 x0_gd, y0_gd = np.array([x0_gd, y0_gd]) - eta * df(x0_gd, y0_gd) x_gd.append(x0_gd) y_gd.append(y0_gd) # Momentumの更新 update = eta * df(x0_mom, y0_mom) + alpha * pre_update x0_mom, y0_mom = np.array([x0_mom, y0_mom]) - update pre_update = update x_mom.append(x0_mom) y_mom.append(y0_mom) # AdaGradの更新 h0 = h0 + df(x0_adagrad, y0_adagrad) ** 2 x0_adagrad, y0_adagrad = np.array([x0_adagrad, y0_adagrad]) - eta_adagrad\ * (1 / np.sqrt(h0)) * df(x0_adagrad, y0_adagrad) x_adagrad.append(x0_adagrad) y_adagrad.append(y0_adagrad) print(i) # 軌跡描画用計算 x_gd = np.array(x_gd) y_gd = np.array(y_gd) z_gd = f(x_gd, y_gd) x_mom = np.array(x_mom) y_mom = np.array(y_mom) z_mom = f(x_mom, y_mom) x_adagrad = np.array(x_adagrad) y_adagrad = np.array(y_adagrad) z_adagrad = f(x_adagrad, y_adagrad) # 基準関数の表示用 x = np.arange(-10, 11, 2) y = np.arange(-10, 11, 2) X, Y = np.meshgrid(x, y) Z = f(X, Y) # ここからグラフ描画---------------------------------------------------------------- # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # グラフの入れ物を用意する。 fig = plt.figure() ax1 = Axes3D(fig) # 軸のラベルを設定する。 ax1.set_xlabel('x') ax1.set_ylabel('y') ax1.set_zlabel('z') ax1.view_init(elev=60, azim=-30) # データプロットする。 ax1.plot_wireframe(X, Y, Z, label='f(x, y)') ax1.scatter3D(x_gd, y_gd, z_gd, label='GD', color='blue', s=50) ax1.scatter3D(x_mom, y_mom, z_mom, label='Momentum', color='red', s=50) ax1.scatter3D(x_adagrad, y_adagrad, z_adagrad, label='AdaGrad', color='green', s=50) # グラフを表示する。 plt.legend() plt.show() plt.close() |
実行結果
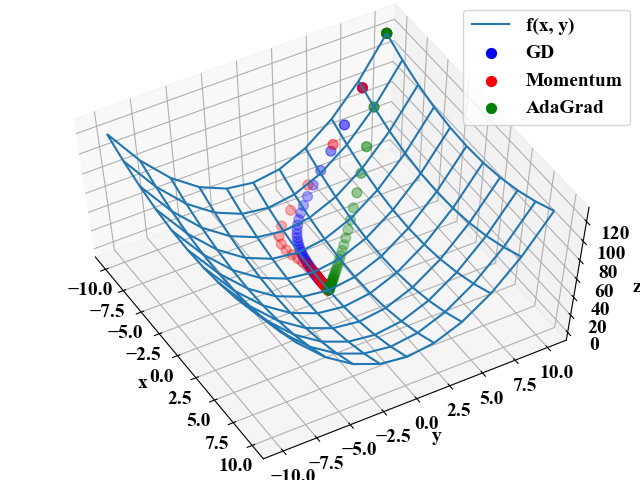
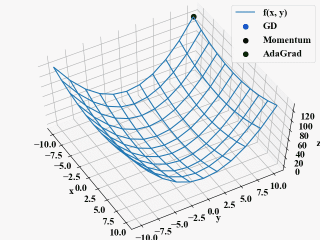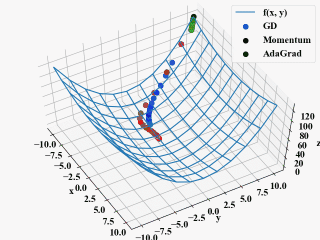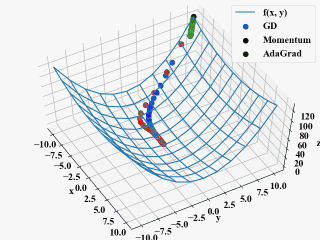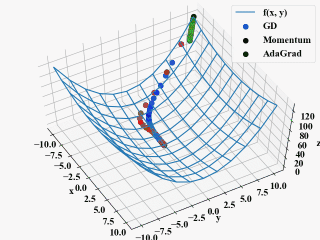
以下が実行結果です。
AdaGradはGDやMomentumと比べ最初から最適解に向かって降下している結果を得ました。
疑問点
以下は「勾配降下法に慣性項を追加するMomentumをPythonで実装」と同じようにGIF動画にしてみた結果で、確かに重み毎に学習率が調整されるAdaGradとしては欲しかった挙動です。
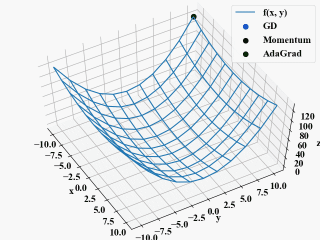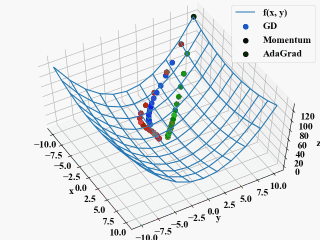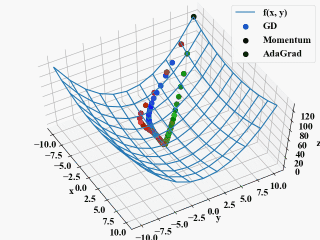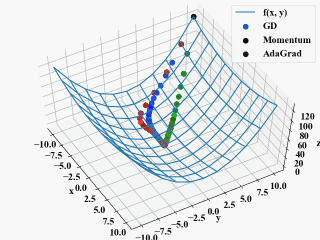
しかし、ここで疑問点。
コード内ではAdaGradだけ\(\eta=2\)としている所にお気付きでしょうか？こうしなかったら更新が遅すぎて全然最適解に行きませんでした。こんなもんなのでしょうか？（式が間違っている？）
てっきり学習率は同じにしても他の手法と比べ改善がみられるような点があると思っていましたが、通常\(\eta=2\)なんて使うかどうか疑問に感じました…。
ちなみに、以下の動画がAdaGradの学習率をGDやMomentumと同じ\(\eta=0.1\)にしたもの。
方向は良いのですが、非常にじれったい。これがハイパーパラメータの調整というものなのでしょうか（ちょっと不安）。
まとめ
本記事では勾配降下法(GD)、Momentumに引き続き、AdaGradをNumpyで書いてみました。まだまだ手探りで「ゼロつく(書籍)」のようにかっこよく書いたりは出来ませんでしたが、それぞれ狙った動きはしているのかなという所感です。
AdaGradは各重み毎に学習率を調整し、さらにハイパーパラメータが1つしかないというメリットがあることがわかりました。
まだ理解はあやしいので、以下の「ゼロから作るDeep Learning」を読み込んでいく必要があると感じました。
最後は少し疑問点が発生し、だんだん難しくなってきたようですが、更新式を〇〇したらどういう挙動になるか…というのが少し見えて来ました！
Twitterでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています！