
機械学習でよく使われる関数の最小値を探す最適化には様々な手法があります。ここでは勾配降下法を少し改善したMomentum(モメンタム)の式とPythonコードを紹介します。
こんにちは。wat(@watlablog)です。本記事では勾配降下法の派生手法であるMomentumを学習していきいます!
Momentumの概要
勾配降下法の更新式
勾配降下法について不明点がある方は、「Pythonで1変数と2変数関数の勾配降下法を実装してみた」で1変数の式からできるだけわかりやすく説明しましたので、まずはそちらをご確認下さい。
ここでは先ほどの記事で紹介している標準的な勾配降下法の更新式を式(1)に示します。
$$\mathbf{x}_{i+1}=\mathbf{x}_{i}-\eta \nabla f (1)$$
この更新式は学習率\(\eta\)が勾配にかかっているだけでとてもシンプルですが、学習の進捗に応じて単調な変化しかしません。
そして一度勾配がフラットに近くなると急激に変化量が少なくなるので、計算時間がかかる割にはちょっとした局所最適解にもはまりやすいというデメリットがあります。
Momentumは更新式を一部変更することでこの問題を改善します。
前回の更新量を利用して慣性項を追加する
Momentumの更新式は式(2)です。
$$\mathbf{x}_{i+1}=\mathbf{x}_{i}-\eta \nabla f + \alpha \Delta \mathbf{w} (2)$$
この式は先ほどの基礎式の右辺最後に係数\(\alpha\)と前回の更新量である\(\Delta \mathbf{w}\)の積を加えている所が違いになります。
この\(\alpha \Delta \mathbf{w}\)は変化量に対して係数がかかっているので、運動方程式で言う所の慣性項と同等の意味を持ちます。
慣性項とは、ある質点に外力が働かなくなっても動き続けようという性質のことで、ニュートンの運動法則の1つです。
言葉で説明するよりも動画を見た方が理解が早いと思いますので、以下のGIF動画をご覧下さい。
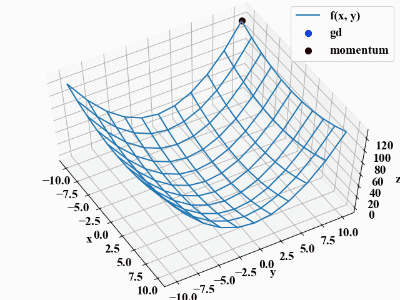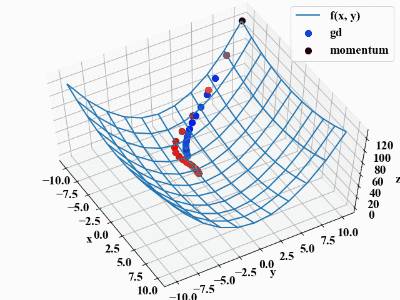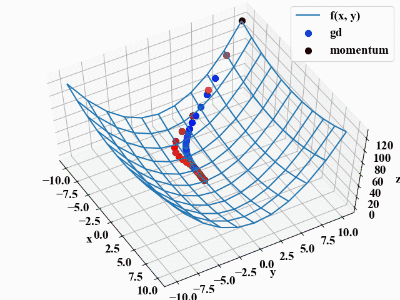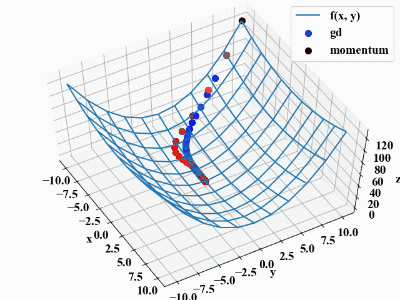
この動画はシンプルな勾配降下法と今回コーディングするMomentumの比較です。降下する関数は式(3)です。
$$z=\frac{1}{4}x^{2}+y^{2} (3)$$
この関数は\(x\)軸方向も緩やかなカーブを描いているので、表示されている平面の中心が最小値です。
赤い点がMomentumとなりますが、GD(勾配降下法)よりも速く最小値に到達していることがわかります。
また、\(y=0\)に到達した瞬間はオーバーランしている慣性項の特徴も確認されました。
今回はこのMomentumをPythonでコーディングします。
Momentumのメリットとデメリット
Momentumは単純なGDが持つ急激な変化(緩やかな勾配ですぐに変化量が小さくなること)をできるだけしないようにハイパーパラメータを調整することができます。
滑らかな変化量とすることで計算の効率を向上させたり、ちょっとしたくぼみを乗り越えたり、より最適な解へ到達しやすくなるメリットがあります。
しかし、\(\eta\)の他に\(\alpha\)と2つのハイパーパラメータに増えたことで、その調整が容易ではなくなるというデメリットも持ちます。
現代では日々最適化問題を効率良く解くためのテクニックが研究されていますが、ここでは基礎からの理解としてまずはこのMomentumをPythonで書いていきたいと思います。
Momentumで最小値を探すPythonコード
全コード
以下のコードはGDとMomentumを比較するためのPythonコードです。それぞれの手法で更新式以外はほとんど同じであり、書き方も「Pythonで1変数と2変数関数の勾配降下法を実装してみた」で紹介した時とほぼ変わっていません。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 |
import numpy as np from matplotlib import pyplot as plt from mpl_toolkits.mplot3d import Axes3D # グラフプロット用基準関数 def f(x, y): z = (1/4) * x ** 2 + y ** 2 return z # 基準関数の微分 def df(x, y): dzdx = (1/2) * x dzdy = 2 * y dz = np.array([dzdx, dzdy]) return dz # 共通のパラメータ max_iteration = 50 # 最大反復回数 eta = 0.1 # 学習率 # GDのパラメータ x0_gd = -10 y0_gd = 10 x_gd = [x0_gd] y_gd = [y0_gd] # Momentumのパラメータ alpha = 0.5 x0_mom = -10 y0_mom = 10 x_mom = [x0_mom] y_mom = [y0_mom] pre_update = np.array([0, 0]) # 最大反復回数まで計算する for i in range(max_iteration): # GDの更新 x0_gd, y0_gd = np.array([x0_gd, y0_gd]) - eta * df(x0_gd, y0_gd) x_gd.append(x0_gd) y_gd.append(y0_gd) # Momentumの更新 update = eta * df(x0_mom, y0_mom) + alpha * pre_update x0_mom, y0_mom = np.array([x0_mom, y0_mom]) - update pre_update = update x_mom.append(x0_mom) y_mom.append(y0_mom) print(i) # 軌跡描画用計算 x_gd = np.array(x_gd) y_gd = np.array(y_gd) z_gd = f(x_gd, y_gd) x_mom = np.array(x_mom) y_mom = np.array(y_mom) z_mom = f(x_mom, y_mom) # 基準関数の表示用 x = np.arange(-10, 11, 2) y = np.arange(-10, 11, 2) X, Y = np.meshgrid(x, y) Z = f(X, Y) # ここからグラフ描画---------------------------------------------------------------- # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # グラフの入れ物を用意する。 fig = plt.figure() ax1 = Axes3D(fig) # 軸のラベルを設定する。 ax1.set_xlabel('x') ax1.set_ylabel('y') ax1.set_zlabel('z') ax1.view_init(elev=60, azim=-30) # データプロットする。 ax1.plot_wireframe(X, Y, Z, label='f(x, y)') ax1.scatter3D(x_gd, y_gd, z_gd, label='gd', color='blue', s=50) ax1.scatter3D(x_mom, y_mom, z_mom, label='momentum', color='red', s=50) # グラフを表示する。 plt.legend() plt.show() plt.close() |
今回、反復計算中の前回のベクトル更新量としてupdateという変数を用いましたが、このupdateにどこまで含めるのが正解なのかの解釈ができていません。もしかしたら正式のものとはちょっと違う可能性があります。
僕は以下の書籍P164の式を読んで今回のコードを書きました。時間があればもっとゆっくり読んだり、他の文献を見たりしてみたいと思います。
実行結果
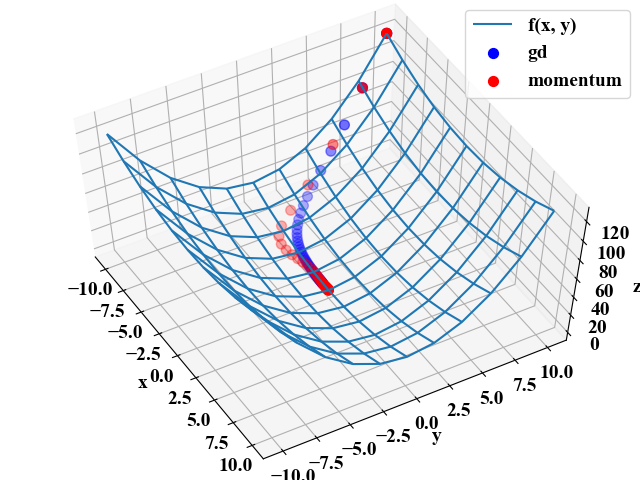
以下が実行結果です。同じ学習率でも慣性項がある方が若干早く最適解に到達していますね。
おまけ:軌跡を画像にする
ちなみに、先ほどの動画はPythonのmatplotlibを静止画にしてフリーソフトでGIFにしただけです。今回のコードで静止画を保存する方法は以下のコードに載せておきます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 |
import numpy as np from matplotlib import pyplot as plt from mpl_toolkits.mplot3d import Axes3D # グラフプロット用基準関数 def f(x, y): z = (1/4) * x ** 2 + y ** 2 return z # 基準関数の微分 def df(x, y): dzdx = (1/2) * x dzdy = 2 * y dz = np.array([dzdx, dzdy]) return dz # 共通のパラメータ max_iteration = 50 # 最大反復回数 eta = 0.1 # 学習率 # GDのパラメータ x0_gd = -10 y0_gd = 10 x_gd = [x0_gd] y_gd = [y0_gd] # Momentumのパラメータ alpha = 0.85 x0_mom = -10 y0_mom = 10 x_mom = [x0_mom] y_mom = [y0_mom] pre_update = np.array([0, 0]) # 最大反復回数まで計算する for i in range(max_iteration): # GDの更新 x0_gd, y0_gd = np.array([x0_gd, y0_gd]) - eta * df(x0_gd, y0_gd) x_gd.append(x0_gd) y_gd.append(y0_gd) # Momentumの更新 update = eta * df(x0_mom, y0_mom) + alpha * pre_update x0_mom, y0_mom = np.array([x0_mom, y0_mom]) - update pre_update = update x_mom.append(x0_mom) y_mom.append(y0_mom) print(i) # 軌跡描画用計算 x_gd = np.array(x_gd) y_gd = np.array(y_gd) z_gd = f(x_gd, y_gd) x_mom = np.array(x_mom) y_mom = np.array(y_mom) z_mom = f(x_mom, y_mom) # 基準関数の表示用 x = np.arange(-10, 11, 2) y = np.arange(-10, 11, 2) X, Y = np.meshgrid(x, y) Z = f(X, Y) # ここからグラフ描画---------------------------------------------------------------- # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # グラフの入れ物を用意する。 fig = plt.figure() ax1 = Axes3D(fig) # 軸のラベルを設定する。 ax1.set_xlabel('x') ax1.set_ylabel('y') ax1.set_zlabel('z') ax1.view_init(elev=60, azim=-30) # データプロットする。 ax1.plot_wireframe(X, Y, Z, label='f(x, y)') for j in range(len(x_mom)): print(j) if j == 0: ax1.scatter3D(x_gd[j], y_gd[j], z_gd[j], label='gd', color='blue', s=50) ax1.scatter3D(x_mom[j], y_mom[j], z_mom[j], label='momentum', color='red', s=50) else: ax1.scatter3D(x_gd[j], y_gd[j], z_gd[j], color='blue', s=50) ax1.scatter3D(x_mom[j], y_mom[j], z_mom[j], color='red', s=50) plt.legend() path = str("{:05}".format(j)) + '.png' plt.savefig(path) # グラフを表示する。 plt.show() plt.close() |
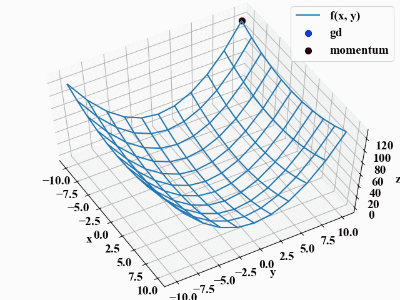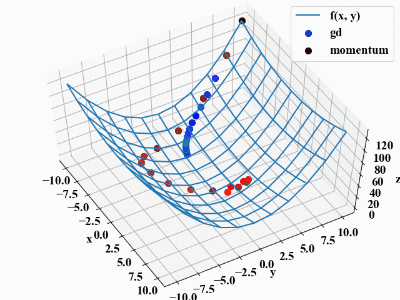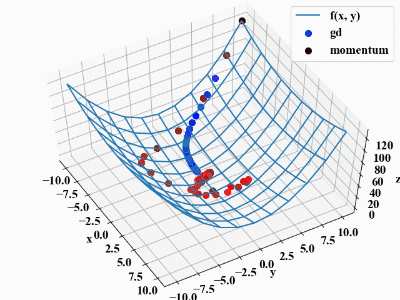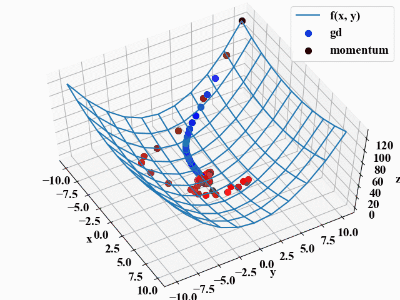
上記コードはalphaの値を高めに設定しているため、下図のような挙動になります。やりすぎると慎重派のGDの方が優秀であるといった結果にもなりますね。
まとめ
今回は基礎的な勾配降下法を少し改良したMomentumの式を学びました。
Momentumは運動量というその名の通り、まるで慣性が働いているかのような最適化手法であることがわかりました。
Pythonコードもこれまでの記述方法と全く同じなので特に難しさは感じませんでしたが、最適化手法というのは非常に奥が深いとも感じました。
様々な最適化手法がありますが、万能な方法は今の所なく、今回のMomentumもハイパーパラメータの調整を必要とします。
ちょっとした式の違いでこれだけ挙動が変わるのは大変面白いですね!Twitterでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています!

 ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!
ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!

コメント