
k近傍法(kNN法)は数ある機械学習手法の中でも簡単なアルゴリズムを持っています。ここではkNN法の概要とPython/scikit-learnによるコードで実際に簡単な分類問題を解く方法を習得することを目標とします。
こんにちは。wat(@watlablog)です。機械学習シリーズも数が増えて来ました!今回はkNN法の概要とPython/scikit-learnの分類コードを紹介します!
k近傍法の概要
k近傍法とは?
k近傍法(kNN法:k-Nearest Neighbor Algorithm)とは、教師あり学習の一種で、最も近いk個のサンプルを使ってテストデータのクラスを予測する分類手法です。
ここで、kは個数を意味する整数です。
回帰に使う場合はk個のサンプルの平均値をとり、分類でも回帰でも使用することができます。
また、kNN法はあらゆる機械学習法の中で最も単純と言われており、得られた結果を第三者に説明しやすい手法です。
決定木も可視化することで説明しやすかったけど、kNNはもっと簡単そうですね!
→決定木の記事はこちら
kNN法の概略図を以下に示します。この図は特徴量\(x\)と\(y\)で表現された2クラス問題で、テストデータが1つ与えられた状況を表しています。
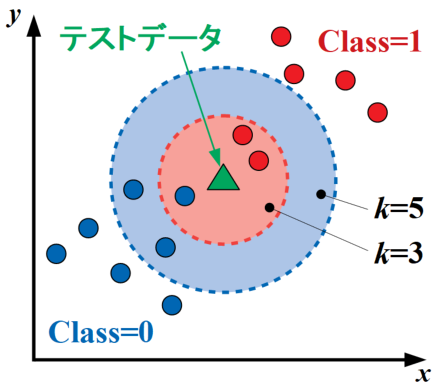
ここで、\(k\)=3の場合はテストデータから最も近い3点のデータを参照し、テストデータはその中で最も多いclass=1に分類されます。
しかし、\(k\)=5とパラメータを変更するとテストデータから最も近い5点を参照するため、今度はclass=0に分類されます。
このように、kNN法は\(k\)というハイパーパラメータを使って「近くのクラスと似ている」という予測方法をとっています。
2クラス問題の場合で\(k\)=2、3クラス問題で\(k\)=3といった場合には判別領域にそれぞれのクラスが同数入ってしまうことになりますが、その場合は判別できないため、ランダムでクラスを決める方法をとる場合があるとのこと。
k近傍法の欠点~次元の呪い
学習時(.fit時)ではなくテストデータを入れた予測時(.predict時)に全サンプルの距離を計算するので、サポートベクターマシンやランダムフォレストといった他の学習手法と異なり予測時の計算時間が長くなる欠点を持っています。
このことから、kNN法は特徴量の次元が増えると計算時間が指数関数的に増加する次元の呪いの影響をダイレクトに受けてしまいます。
また、kNN法における次元の呪いの最大の問題点は、次元が増えると漸近仮定が成立しなくなってくることにあります。
詳細の式展開や証明は専門書に任せるとし、ここではイメージだけを説明したいと思います。
3次元空間の物体を4次元空間…N次元空間とどんどん高次元空間にマッピングしていくと、密度のほとんどが表面に分布していくというHigh-Dimensional Probabilityの理論(参考論文はこちら, シミュレーションで確かめた素晴らしいQiita記事もありました)があります。

これだけで衝撃的なことですが、kNN法はテストデータの近傍点を探索するアルゴリズムなので、一様に分布しているデータでさえも高次元になればなるほど全てのデータ点の距離が同程度になってしまうため、高次元データに対する適用には向いていません。
kNN法の派生アルゴリズム
単純なkNN法ですが、基本の考え方から少し修正した派生アルゴリズムがいくつかあります。ここではその概要を紹介します。
変形kNN法(modified kNN)
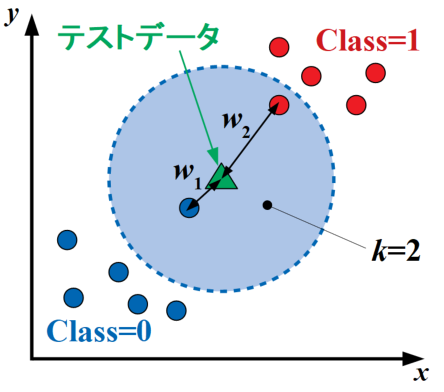
変形kNN法(modified kNN)は、通常のkNN法が個数のみをテストデータの分類判断指標に使うのに対し、距離に応じて重みを付ける精度改善を狙ったアルゴリズムです。
以下の図のテストデータをmodified kNNのアルゴリズムで計算すると、距離が近いclass=0に分類されます。
誤り削除型kNN法(edited kNN)
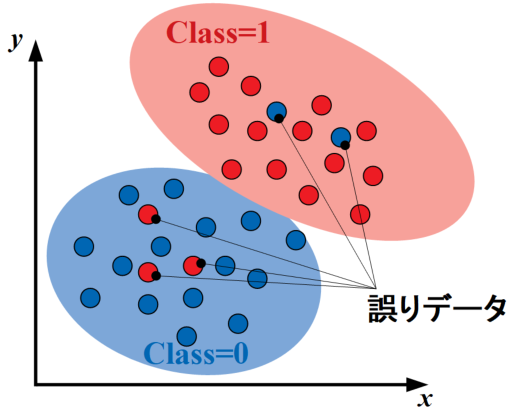
誤り削除型kNN法(edited kNN)とは、決定境界を構築した後に誤分類されている誤りデータを削除するという計算負荷低減を狙った改善アルゴリズムです。
実際のデータは100%分類可能な決定境界が引けることは稀で、以下の図のように誤りデータを含みます。このような誤りデータをデータセットから削除することで、探索時間を削減することができます(データの削除は反復的に行う場合もあるとのこと)。
圧縮型kNN法(condensed kNN)
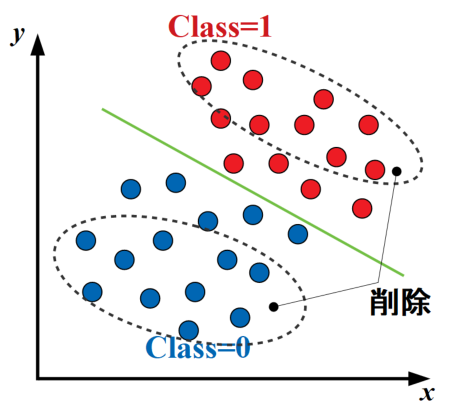
圧縮型kNN(condensed kNN)とは、決定境界付近以外のデータを予め削除しておくことで計算負荷低減を狙った改善アルゴリズムです。
以下の図のように、ある程度密なデータの場合分類精度に影響を与えていないデータを削除しておくことで、テストデータと各点の全点探査回数を激減させることができます。
分枝限定法
分枝限定法とは、分枝法と限定法を使ってデータの近傍探査効率化を図ることで計算負荷低減を狙った改善アルゴリズムです。
分枝法とは、データを木構造としてクラスタリングする手法のことで、データを1つ1つの集合と考えます。集合(クラスタ)として考えられたデータはクラスタ内の平均ベクトル等を計算することができます。木構造とすることで、上位クラスタ、下位クラスタと組織化することが可能です。
限定法とは、テストデータが与えられた時、まず上位クラスタとの距離を計算しおおまかに近いクラスタを特定した後に近傍のデータを調べる手法です。こうすることで、他の上位クラスタに含まれるデータセットに対する距離計算を省くことができます。
近似最近傍探索法
近似最近傍探索とは、厳密な解を求めず、近似解を許容することで計算負荷低減を狙った改善アルゴリズムです。
この方法はまず始めに距離の近似解を設定し、その近似解内のデータで最良優先探索(Best-First Search)を行います。
最良優先探索では、テストデータを予め適当なクラスに分類しておき、計算に使うデータ点を使って2分木による領域分割を行い、それぞれの領域内のデータと距離を比較していく手法をとります。
中々沢山の改良アルゴリズムがあり、特に最後2つは図で説明するのが難しいのでまだまだ理解が足らない様子!以下の「はじめてのパターン認識」という本に各種機械学習の理論概要が載っているので、もっと勉強せねば!
k近傍法のハイパーパラメータ(scikit-learn)
n_neighbors
近傍点の個数を設定します。kNN法では最も重要なハイパーパラメータです。この\(k\)値によって分類結果が大きく左右されます。
デフォルトは\(k\)=5。
weights
重みの設定を行います。デフォルトは'uniform'となり全ての点の距離に対する重みは等価です。
'distance'と設定することで距離に応じて重みがかかるmodified kNNになります。
その他ハイパーパラメータも多数ありますが、詳しくは公式ページを参照下さい。
公式ページ:sklearn.neighbors.KNeighborsClassifier
scikit-learnにはweightsパラメータがあるからmodified kNNはできるけど、condenced kNNとか分枝限定法、近似最近傍法に関する記述が見つからないぞ?パッケージとしては無いのかな?
PythonによるkNN法クラス分類コード
全コード
以下にkNN法による3クラス分類問題のコードを示します。データセットは「Python/sklearnで決定木分析!分類木の考え方とコード」で使ったものと同じで、コードの内容もほぼ同じなので、import文とKNeighborsClassifierを使う部分が異なるだけとなります。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 |
import numpy as np import pandas as pd from sklearn.neighbors import KNeighborsClassifier from matplotlib import pyplot as plt # データを用意する------------------------------------------ df = pd.DataFrame() # データフレーム初期化 n = 20 # 1クラス毎のデータ数 for i in range(3): # データ作成ループ if i == 0: x = pd.Series(np.random.uniform(0.5, 2.8, n)) y = pd.Series(x * np.random.uniform(0.8, 1.2, n)) elif i == 1: x = pd.Series(np.random.uniform(2.2, 3.8, n)) y = pd.Series(np.random.uniform(0.5, 1.8, n)) else: x = pd.Series(np.random.uniform(3.2, 3.8, n)) y = pd.Series(np.random.uniform(2.2, 3.8, n)) label = pd.Series(np.full(n, i)) # ラベル(クラス)を作成 temp_df = pd.DataFrame(np.c_[x, y, label]) # クラス毎のデータフレームを作成 df = pd.concat([df, temp_df]) # 作成されたクラス毎のデータを逐次結合 df.index = np.arange(0, len(df), 1) # index(行ラベル)を初期化 # クラス毎のデータフレームに分離(プロット用) class_0 = df[df[2] == 0] # ラベル0を抽出 class_1 = df[df[2] == 1] # ラベル1を抽出 class_2 = df[df[2] == 2] # ラベル1を抽出 # ---------------------------------------------------------- # 学習させる値(訓練データ)とクラス(正解ラベル)に分離 data = df[[0, 1]] # 訓練データ data_class = pd.Series(df[2]) # 正解ラベル # 決定木による学習 clf = KNeighborsClassifier(n_neighbors=5) # kNN法オブジェクトを定義 clf.fit(data, data_class) # フィッティング # 決定境界可視化用 grid_line = np.arange(-10, 10, 0.05) # グリッドデータのための配列を生成 X, Y = np.meshgrid(grid_line, grid_line) # グリッドを作成 Z = clf.predict(np.array([X.ravel(), Y.ravel()]).T) # .predictが使えるデータshapeに変換して予測 Z = Z.reshape(X.shape) # 3Dプロットするためにshapeを再変換 r2 = clf.score(data, data_class) # 決定係数を算出 # ここからグラフ描画---------------------------------------- # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' fig = plt.figure() ax1 = plt.subplot(111) # グラフの上下左右に目盛線を付ける。 ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('x') ax1.set_ylabel('y') # スケールの設定をする。 ax1.set_xlim(0, 4) ax1.set_ylim(0, 4) # データプロットする。 ax1.contourf(X, Y, Z, cmap='coolwarm') ax1.scatter(class_0[0], class_0[1], label='class=0', edgecolors='black') ax1.scatter(class_1[0], class_1[1], label='class=1', edgecolors='black') ax1.scatter(class_2[0], class_2[1], label='class=2', edgecolors='black') plt.text(0.5, 2.2, '$\ R^{2}=$' + str(round(r2, 2)), fontsize=20) plt.legend() # グラフを表示する。 plt.show() plt.close() # ---------------------------------------------------------- |
実行結果
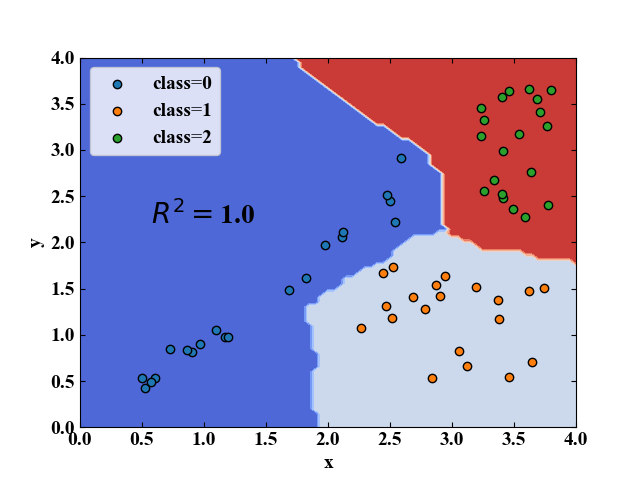
このコードを実行すると以下の図を得ます。kNN法による決定境界の描画をすることができました。
まとめ
本記事では、教師あり機械学習アルゴリズムの1つであるk近傍法(kNN法)の概要を説明し、その特徴や派生アルゴリズムについて紹介しました。
また、Python/scikit-learnによる計算コードを紹介し、3クラス分類ができることを確認しました。

 ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!
ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!

コメント