Python/SciPyで波形リサンプリング!任意時間軸に補間!

実験や解析でデータを波形として取得した場合、波形はあるサンプリングレートで収録されている場合や、不等ピッチの時間刻みである場合等様々です。今回はデータ解析時に波形のサンプリングを変更するリサンプリング方法を紹介します。

こんにちは。wat(@watlablog)です。実験屋さん、CAE屋さんも波形のリサンプリング需要は結構あるのではないでしょうか？
今回はSciPyを使った波形の任意時間軸へのリサンプリング方法を紹介します！

前半はリサンプリングの基本について説明しています。手っ取り早くコードを確認したい方は目次からジャンプしてみて下さい。

目次（項目クリックでジャンプできます）

波形リサンプリングとは？

サンプリングレートのおさらい

波形リサンプリングとは、一度収録した実験データやシミュレーション結果を再度サンプリングし直すことを意味しています。

特に、当WATLABブログの「信号処理」カテゴリではデジタル信号の処理を多くしていますが、その大部分にサンプリングレートという言葉が出て来ました。

「Pythonでwav波形を切り出す！NumPyの配列処理」という記事では、以下の図を使って波形の計測データ点とサンプリングレート、時間刻み幅の関係を説明しました。

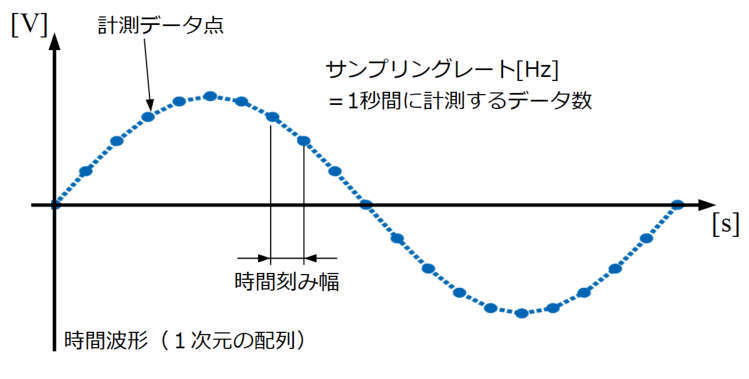
このようにサンプリングされた波形は連続した関数ではなく、離散化された1次元の配列に過ぎません。

ここではサンプリングレートの逆数がそれぞれのデータポイント間の時間刻み幅であることを示しています。

では、リサンプリングを図で説明してみましょう。

リサンプリングとは新しい時間刻み幅を設定して補間すること

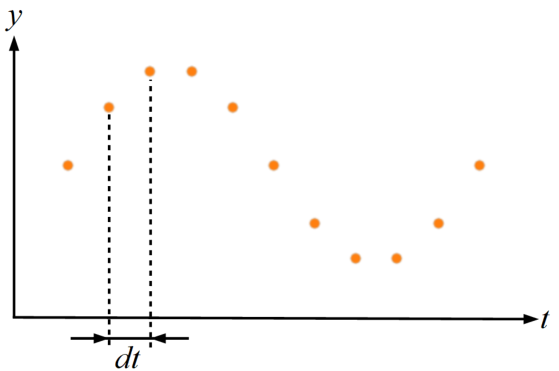
まずは通常の実験データのように時間刻み幅 $d t$ でサンプリングされた時間波形を以下の図に示します。

次に、上記グラフをリサンプリングした後の時間波形図を以下に示します。

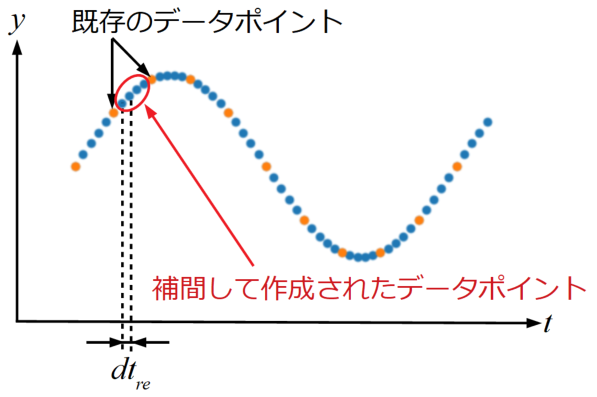
初期からある既存のデータポイントをオレンジの点で示しています。

オレンジの点の間は本来何も無い部分でしたが、新規時間刻み幅 $d t_{r e}$ で再度サンプリングする時は、この既存のデータポイント間を補間して埋めていきます。

このように、元々の時間刻み幅 $d t$ よりも新規時間刻み幅 $d t_{r e}$ が小さくなっているということは、逆数であるサンプリングレートが上がっている（1秒当たりに取得するデータ数が多くなる）ということを意味し、このようなリサンプリングのことをアップサンプリングと呼びます。

逆に、サンプリングレートが下がるようなリサンプリングのことをダウンサンプリングと呼び、リサンプリングする時に呼び方を使い分けます。

次はリサンプリングの主なメリットを紹介します。

波形リサンプリングの3つのメリット

①細かくサンプリングし直す事で点と点の間の数値を算出できる

波形をリサンプリングするのはざっと上げるだけで主に3つのメリットがあります。

1つ目はアップサンプリングをすることで間の点の数値を算出できる点にあります。

例えば、0[s]から10[s]まで1[s]ずつ記録されたデータがあった場合、仮に5.5[s]の時の値を知りたい時は、四捨五入して6[s]のデータを参照するでしょうか？

この場合は0.5[s]や0.1[s]の時間刻み幅でアップサンプリングを行えば点と点の間を補間してくれるので、より実際に近い目的の値を得ることができるメリットがあります。

②粗くサンプリングし直す事でデータサイズを軽くできる

アップサンプリングの逆でサンプリングレートを元の値よりも低くするダウンサンプリングというものがあります。

仮にデータ点数が1000点の測定結果を1\10の100点にダウンサンプリングした場合、これはデータ容量が軽くなるメリットがあります。

例えば、数百[Hz]の振動現象と時定数の低い温度変化を同時にロガーで収録した場合、後処理で温度の情報だけ使いたい時は、振動現象と同じサンプリングである必要はありません。

そんな時は必要な情報が十分表現できる最低限のサンプリングレートでダウンサンプリングをしてみましょう。

③不等ピッチ時間軸を等ピッチに変換できる

特にシミュレーション結果のデータに多いと思いますが、時間軸の配列が等ピッチではない不等ピッチデータになっている場合があります。

シミュレーションには、勾配の激しい所を細かいサンプリングで、変化の少ない所を粗いサンプリングで計算するアルゴリズムもあります。

後でFFT等の信号処理をする場合のために、リサンプリングで等ピッチに変えるメリットは大変重宝しますね！

PythonのSciPyで簡単リサンプリング!

直線補間

以下のコードにリサンプリングの全コードを示します。

基本はinterpolate.interp1dで元となるデータの保管関数fを作成しておき、その関数に任意のサンプリングで作成した時間軸t_resampleを割り当て、リサンプリング波形を生成するという流れです。

ここでは補間の仕様kind='linear'と直線補間としています。これは元波形のデータポイントの間を直線で補間することを意味しています。

サンプルとなる波形は「Pythonで滑らかに振幅増加する正弦波を作る1つの簡単な例」で紹介した振幅がスムースに増加していく正弦波です。

import numpy as np
from scipy import interpolate
from matplotlib import pyplot as plt

# ここからサンプルとなる波形の作成-------------
# スムース関数
def smooth(x):
    a = 30
    y = np.tanh(x) / (1 + a * np.exp(- x))
    return y

A = 1    # 振幅
t0 = 0   # 初期時間[s]
tf = 10  # 終了時間[s]
dt = 0.2 # 時間刻み[s]
f = 1    # 周波数[Hz}
t = np.arange(t0, tf + dt, dt)  # 時間軸

# 滑らかに振幅増加する正弦波
y = smooth(t) * A * np.sin(2 * np.pi * f * t)
# ここまでサンプルとなる波形の作成-------------

# 補間関数fを作成
f = interpolate.interp1d(t, y, kind='linear')

# 補間した結果からリサンプリング波形を生成
num = 10000
t_resample = np.linspace(t0, tf, num)
y_resample = f(t_resample)              # f(t)

# ここからグラフ描画
# フォントの種類とサイズを設定する。
plt.rcParams['font.size'] = 14
plt.rcParams['font.family'] = 'Times New Roman'

# 目盛を内側にする。
plt.rcParams['xtick.direction'] = 'in'
plt.rcParams['ytick.direction'] = 'in'

# グラフの上下左右に目盛線を付ける。
fig = plt.figure()
ax1 = fig.add_subplot(111)
ax1.yaxis.set_ticks_position('both')
ax1.xaxis.set_ticks_position('both')

# 軸のラベルを設定する。
ax1.set_xlabel('Time [s]')
ax1.set_ylabel('y')

# 軸の範囲設定
ax1.set_xticks(np.arange(0, 20, 1))
ax1.set_yticks(np.arange(-2, 2, 0.5))
ax1.set_xlim(0, 10)
ax1.set_ylim(-1.5, 1.5)

# データプロット
ax1.scatter(t_resample, y_resample, label="resample", s=5)
ax1.scatter(t, y, label="original")

# レイアウトと凡例
fig.tight_layout()
plt.legend(loc='upper left')

# グラフを表示する。
plt.show()
plt.close()

import numpy as np

from scipy import interpolate

from matplotlib import pyplot as plt

# ここからサンプルとなる波形の作成-------------

# スムース関数

def smooth(x):

a = 30

y = np.tanh(x) / (1 + a * np.exp(- x))

return y

A = 1 # 振幅

t0 = 0 # 初期時間[s]

tf = 10 # 終了時間[s]

dt = 0.2 # 時間刻み[s]

f = 1 # 周波数[Hz}

t = np.arange(t0, tf + dt, dt) # 時間軸

# 滑らかに振幅増加する正弦波

y = smooth(t) * A * np.sin(2 * np.pi * f * t)

# ここまでサンプルとなる波形の作成-------------

# 補間関数fを作成

f = interpolate.interp1d(t, y, kind='linear')

# 補間した結果からリサンプリング波形を生成

num = 10000

t_resample = np.linspace(t0, tf, num)

y_resample = f(t_resample) # f(t)

# ここからグラフ描画

# フォントの種類とサイズを設定する。

plt.rcParams['font.size'] = 14

plt.rcParams['font.family'] = 'Times New Roman'

# 目盛を内側にする。

plt.rcParams['xtick.direction'] = 'in'

plt.rcParams['ytick.direction'] = 'in'

# グラフの上下左右に目盛線を付ける。

fig = plt.figure()

ax1 = fig.add_subplot(111)

ax1.yaxis.set_ticks_position('both')

ax1.xaxis.set_ticks_position('both')

# 軸のラベルを設定する。

ax1.set_xlabel('Time [s]')

ax1.set_ylabel('y')

# 軸の範囲設定

ax1.set_xticks(np.arange(0, 20, 1))

ax1.set_yticks(np.arange(-2, 2, 0.5))

ax1.set_xlim(0, 10)

ax1.set_ylim(-1.5, 1.5)

# データプロット

ax1.scatter(t_resample, y_resample, label="resample", s=5)

ax1.scatter(t, y, label="original")

# レイアウトと凡例

fig.tight_layout()

plt.legend(loc='upper left')

# グラフを表示する。

plt.show()

plt.close()

上記コードを実行すると、以下の図を得ます。

元波形より細かいサンプリングの波形を得ることができました。これがアップサンプリングです。

仮に「num=10」と極端にデータポイント数を少なくしてみると、以下のように元波形と比べて疎な波形になります。これがダウンサンプリングです。

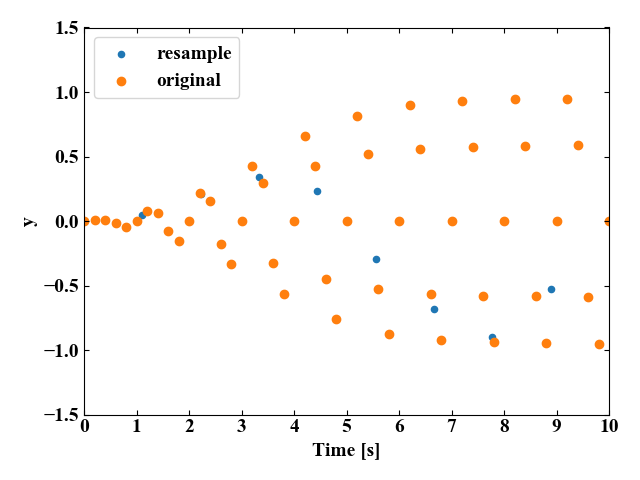
但し、このダウンサンプリングはやりすぎです。サンプリングが粗すぎて元波形の形を完全に損ねてしまっています。高周波数のデータを粗くサンプリングすると本来ありえない低周波の振動が見えてくるエイリアス誤差が発生していますね。

3次スプライン補間

続いて補間の仕様を変えてみましょう。

上記全コードの中で「kind='cubic'」と変更することで、3次のスプライン補間にすることができます。

# 補間関数fを作成
f = interpolate.interp1d(t, y, kind='cubic')

1 2	# 補間関数fを作成 f = interpolate.interp1d(t, y, kind='cubic')

すると先ほどのグラフは以下の図に変化します。

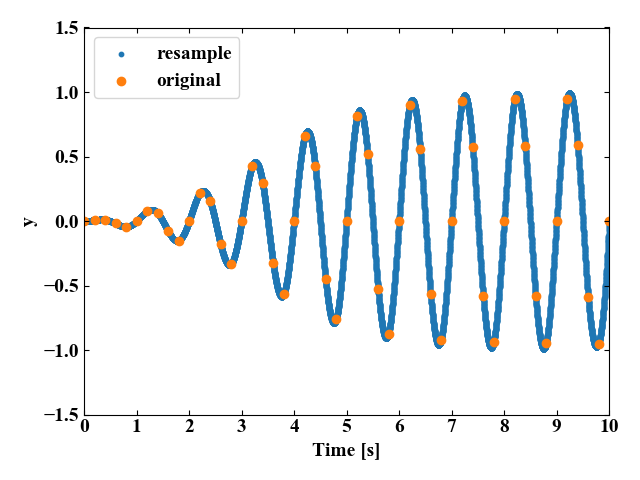
お、この図は元の正弦波にかなり近いぞ！補間の仕方でがらっと見た目が変わるね！

他にも4次スプライン「quadratic」等様々な引数がありますが、是非お手元の開発環境で実行しながら確認してみて下さい。

まとめ

本ページではリサンプリングの概要やメリットを紹介し、実際にサンプル波形を用いて補間とリサンプリングを行いました。

そして補間の仕様を直線やスプラインに変更して結果を確認しました。

最初は自分で作ろうと思ったけど、リサンプリングもライブラリを使えば簡単にできるね！
Twitterでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています！