ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました！
信号を生成する目的は様々あり、中には周波数軸で見た時にある周波数でピークが立ち、その倍数成分が全て高調波として立ってくる波形が欲しい時もあります。ここでは高調波成分がしっかり発生するのこぎり波をPythonで生成する方法を解説します。
こんにちは。wat(@watlablog)です。
今回も信号生成系の記事を書いてみます。ここではPythonを使ったのこぎり波を生成し、その周波数特性を見てみます！
のこぎり波とは？
波形の形
のこぎり波とは、以下のグラフのような時間とともに徐々に直線増加後にストンと落ちる周期波形のことを言います。見た目がのこぎりの刃のようだとのことで、このような名称になっています。鋸歯状波（きょしじょうは）とも呼ばれます。
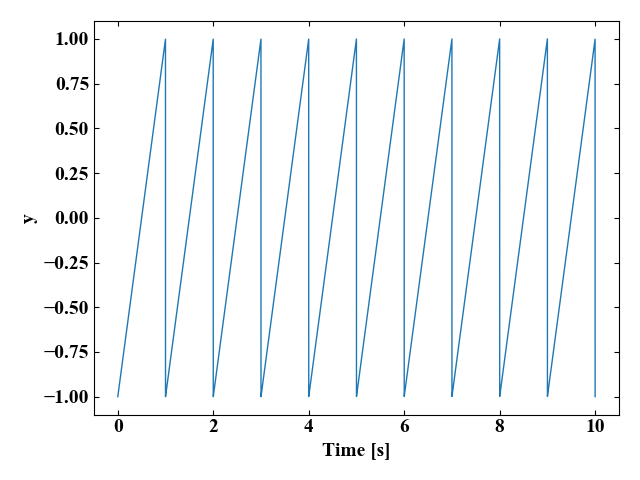
のこぎり波はどんな目的で使われる？
上のグラフのような波形を作って何が面白いのか、と多くの人は思うかもしれませんが、実はのこぎり波は意外と僕達の身近で利用されています。
楽器のシンセサイザーは色々な音を出すことが出来ますが、その基本は周波数軸で見た時の高調波をどの程度含ませるか、という部分にあります。
後程FFTしたのこぎり波を示しますが、のこぎり波は基本次数の倍数で高調波が発生します。この高調波を増減させて色々な音を作り出し、IFFTで時間波形に戻すことで実際に音を発生させることが可能です。
のこぎり波は高調波がすごい！と覚えておけばとりあえず問題は無いでしょう（←？）。
Pythonでのこぎり波を作ってみる
時間波形と周波数波形の特徴
では早速Pythonでのこぎり波を作ってみましょう。SciPyのsignalモジュールの使い方等は「Pythonでチャープ信号！周波数スイープ正弦波の作り方」でやった内容と全く同じなので、詳しくはそちらの記事を参照下さい。
以下がのこぎり波生成とFFT計算をするプログラムコードです。のこぎり波は「# 波形生成」部分のsignal.sawtoothで生成しています。ここでは50Hzの周波数を指定しています。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 |
from scipy import signal from scipy import fftpack import numpy as np import matplotlib.pyplot as plt # オーバーラップ処理 def ov(data, samplerate, Fs, overlap): Ts = len(data) / samplerate # 全データ長 Fc = Fs / samplerate # フレーム周期 x_ol = Fs * (1 - (overlap / 100)) # オーバーラップ時のフレームずらし幅 N_ave = int((Ts - (Fc * (overlap / 100))) / (Fc * (1 - (overlap / 100)))) # 抽出するフレーム数（平均化に使うデータ個数） array = [] # 抽出したデータを入れる空配列の定義 # forループでデータを抽出 for i in range(N_ave): ps = int(x_ol * i) # 切り出し位置をループ毎に更新 array.append(data[ps:ps + Fs:1]) # 切り出し位置psからフレームサイズ分抽出して配列に追加 return array, N_ave # オーバーラップ抽出されたデータ配列とデータ個数を戻り値にする # 窓関数処理（ハニング窓） def hanning(data_array, Fs, N_ave): han = signal.hann(Fs) # ハニング窓作成 acf = 1 / (sum(han) / Fs) # 振幅補正係数(Amplitude Correction Factor) # オーバーラップされた複数時間波形全てに窓関数をかける for i in range(N_ave): data_array[i] = data_array[i] * han # 窓関数をかける return data_array, acf # FFT処理 def fft_ave(data_array, samplerate, Fs, N_ave, acf): fft_array = [] for i in range(N_ave): fft_array.append(acf * np.abs(fftpack.fft(data_array[i]) / (Fs / 2))) # FFTをして配列に追加、窓関数補正値をかけ、(Fs/2)の正規化を実施。 fft_axis = np.linspace(0, samplerate, Fs) # 周波数軸を作成 fft_array = np.array(fft_array) # 型をndarrayに変換 fft_mean = np.mean(fft_array, axis=0) # 全てのFFT波形の平均を計算 return fft_array, fft_mean, fft_axis # 波形生成 samplerate = 25600 x = np.arange(0, 12800)/samplerate data = signal.sawtooth(2 * np.pi * 50 * x) Fs = 4096 # フレームサイズ overlap = 75 # オーバーラップ率 # 作成した関数を実行：オーバーラップ抽出された時間波形配列 time_array, N_ave = ov(data, samplerate, Fs, overlap) # 作成した関数を実行：ハニング窓関数をかける time_array, acf = hanning(time_array, Fs, N_ave) # 作成した関数を実行：FFTをかける fft_array, fft_mean, fft_axis = fft_ave(time_array, samplerate, Fs, N_ave, acf) # ここからグラフ描画 # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure() ax1 = fig.add_subplot(211) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') ax2 = fig.add_subplot(212) ax2.yaxis.set_ticks_position('both') ax2.xaxis.set_ticks_position('both') ax2.set_xticks(np.arange(0, samplerate, 200)) ax2.set_xlim(0, 1000) ax2.set_yscale('log') # 軸のラベルを設定する。 ax1.set_xlabel('Time [s]') ax1.set_ylabel('y') ax2.set_xlabel('Frequency [Hz]') ax2.set_ylabel('y') # データプロットの準備とともに、ラベルと線の太さ、凡例の設置を行う。 ax1.plot(x, data, label='sawtooth', lw=1) ax2.plot(fft_axis, fft_mean, label='sawtooth', lw=1) # レイアウト設定 fig.tight_layout() # グラフを表示する。 plt.show() plt.close() |
そして以下のグラフが結果です。50Hzののこぎり波は、50Hzを基本次数として、その倍数で高調波の次数が立ってきている特徴がわかると思います。
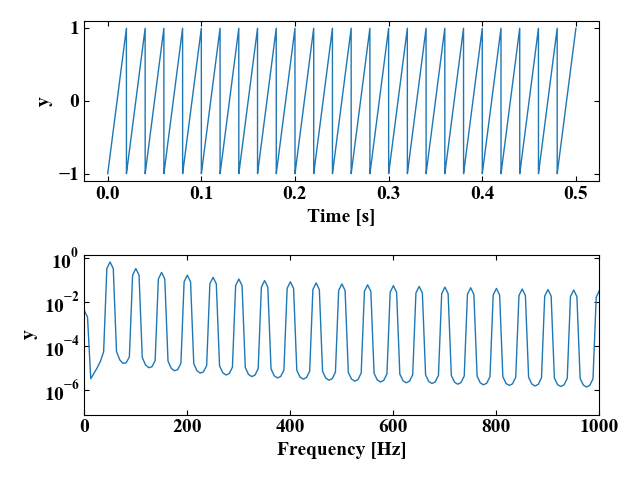
まとめ
本ページでは、のこぎり波の特徴と利用方法について簡単に説明し、Pythonによるコーディング方法を紹介しました。
FFTまで含むコードを紹介し、実際に生成したのこぎり波の周波数特性を観察すると、基本次数の倍数で高調波が発生する特徴を持っていることが確かめられました。
チャープ信号が周波数でフラットな特性を持っている対し、のこぎり波は高調波が発生するという特徴があるんだね！
Twitterでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています！
コメント