画像は全て2次元ですが、見せ方によってはあたかも3次元に存在しているように見せることも可能です。このページではこれまでWATLABブログで習得した内容で事例を紹介します。
こんにちは。wat(@watlablog)です。
画像処理は、特にゲームやエンタメの世界は視覚効果を狙った処理が頻繁に行われています。ここでは、射影変換と楕円方程式を使った視覚効果を紹介します！
2Dを楕円方程式で変形させて回転させる
今回題材にする画像はこちら。以前「Python/OpenCVの射影変換なら簡単に画像補正ができる！」や「Python/OpenCVの適応的閾値処理で綺麗な二値化！」で取り扱った画像です。
白黒、平面と、処理し甲斐のある画像です。
そして今回目指すのが以下のGIF動画です。上の画像は適当に撮影した写真ですが、盤面の図を抽出して斜め上から見ているような視覚効果を出しています。
この処理には「Python/OpenCVで楕円方程式を描画する！」で習得した楕円関数を使っています。楕円パラメータをいじることで次のような斜め上から見る角度を少し変更することも簡単にできます。
楕円パラメータを真円にすることで真上から見ているような効果を出すことも可能です。
この動画を作るために、「Pythonで平面を回転させる効果を表現する！」で習得した複数点を楕円軌道上で動かす方法を使っています。
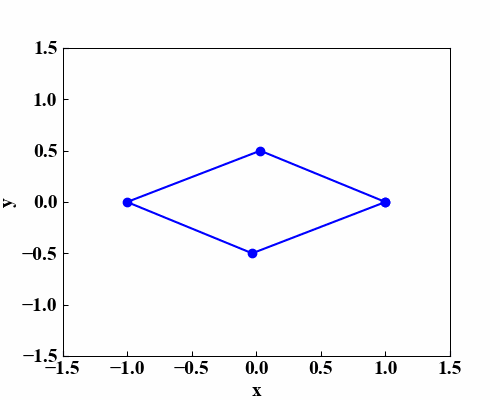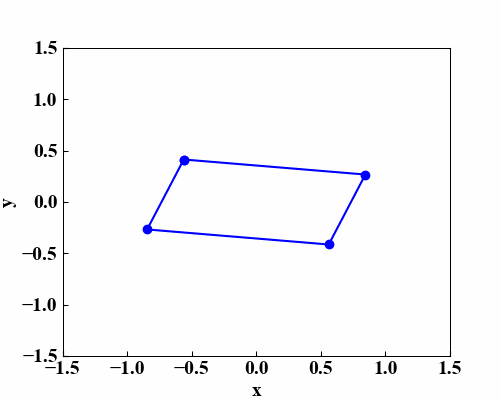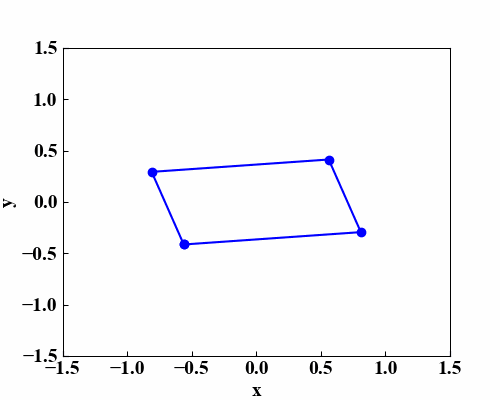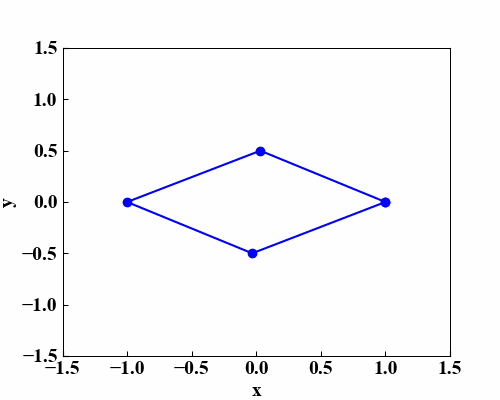
そして4点の座標位置が決まったら「Python/OpenCVの射影変換なら簡単に画像補正ができる！」で使った射影変換を使って画像形状を4点にフィットさせます。
射影変換であれば画像形状は自由自在！これをプログラミングしていきます！
Pythonによるプログラミング
全コード
ほとんどは過去の上で紹介した射影変換と4点アニメーションと同じなので、最初に全コードを紹介しておきます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 |
import numpy as np import cv2 def ellipse(x, a, b, g, ini): y = [] # y値をためる c = ini # y軸の符号スイッチ # 第1象限から第4象限までの全てのy値を計算 for i in range(len(g)): y_single = b * np.sqrt(1 - (np.power(x[i], 2) / np.power(a, 2))) if i == 0: pass elif np.sign(g[i - 1]) == np.sign(g[i]): pass else: c = -1 * c y.append(y_single * c) # y値の符号調整 return y a = 1.0 # 楕円方程式のa b = 0.7 # 楕円方程式のb N = 20 # フレーム分割数 t = np.linspace(-1 * np.pi, np.pi, N) # －π～πまでの範囲 t_inv = np.linspace(np.pi, -1 * np.pi, N) # π～－πまでの範囲 im_size = 250 path = 'igo_pt.png' # 画像のパス img = cv2.imread(path, 0) # 画像読み込み # 位相配列 phase = [np.pi/2, np.pi/100, -1 * np.pi/2, -1 * np.pi/100] # 楕円方程式中で振動させるxとy値の符号判断用に勾配を計算する x = [] g = [] for i in range(4): if i <= 1: x.append(a * np.sin(t - phase[i])) else: x.append(a * np.sin(t_inv - phase[i])) g.append(np.gradient(x[i])) # 楕円方程式のy値を計算する y = [] for j in range(4): if j <= 1: y.append(ellipse(x[j], a, b, g[j], 1)) else: y.append(ellipse(x[j], a, b, g[j], -1)) # 変換前後の対応点を設定 p_original = np.float32([[257, 0], [0, 0], [0, 235], [257, 235]]) path_head = 'out_' path_ext = '.png' for i in range(len(t)): x = np.array(x) y = np.array(y) X1 = int((x[0, i] * im_size / 2) + im_size / 2) X2 = int((x[1, i] * im_size / 2) + im_size / 2) X3 = int((x[2, i] * im_size / 2) + im_size / 2) X4 = int((x[3, i] * im_size / 2) + im_size / 2) Y1 = int((y[0, i] * im_size / 2) + im_size / 2) Y2 = int((y[1, i] * im_size / 2) + im_size / 2) Y3 = int((y[2, i] * im_size / 2) + im_size / 2) Y4 = int((y[3, i] * im_size / 2) + im_size / 2) p_trans = np.float32([[X1, Y1], [X2, Y2], [X3, Y3], [X4, Y4]]) # 変換マトリクスと射影変換 M = cv2.getPerspectiveTransform(p_original, p_trans) i_trans = cv2.warpPerspective(img, M, (257, 235)) if i < 10: path_out = path_head + '0' + str(i) + path_ext else: path_out = path_head + str(i) + path_ext cv2.imwrite(path_out, i_trans) |
射影変換をして動画用の複数画像を作る
以下は射影変換部のコードです。まずは元の画像で平面としたい点をp_originalで指定します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 |
# 変換前後の対応点を設定 p_original = np.float32([[257, 0], [0, 0], [0, 235], [257, 235]]) path_head = 'out_' path_ext = '.png' for i in range(len(t)): x = np.array(x) y = np.array(y) X1 = int((x[0, i] * im_size / 2) + im_size / 2) X2 = int((x[1, i] * im_size / 2) + im_size / 2) X3 = int((x[2, i] * im_size / 2) + im_size / 2) X4 = int((x[3, i] * im_size / 2) + im_size / 2) Y1 = int((y[0, i] * im_size / 2) + im_size / 2) Y2 = int((y[1, i] * im_size / 2) + im_size / 2) Y3 = int((y[2, i] * im_size / 2) + im_size / 2) Y4 = int((y[3, i] * im_size / 2) + im_size / 2) p_trans = np.float32([[X1, Y1], [X2, Y2], [X3, Y3], [X4, Y4]]) # 変換マトリクスと射影変換 M = cv2.getPerspectiveTransform(p_original, p_trans) i_trans = cv2.warpPerspective(img, M, (257, 235)) if i < 10: path_out = path_head + '0' + str(i) + path_ext else: path_out = path_head + str(i) + path_ext cv2.imwrite(path_out, i_trans) |
path_headとpath_extは画像をプログラム的に連番で保存するので、ファイル名を自動的に決定するために使用します。
forループ内のX１～X4、Y１～Y４は画像4隅の4点の座標を指定しています。しかし数学上の座標で設定した楕円の座標はそのまま画像上の座標にプロットすることはできません。
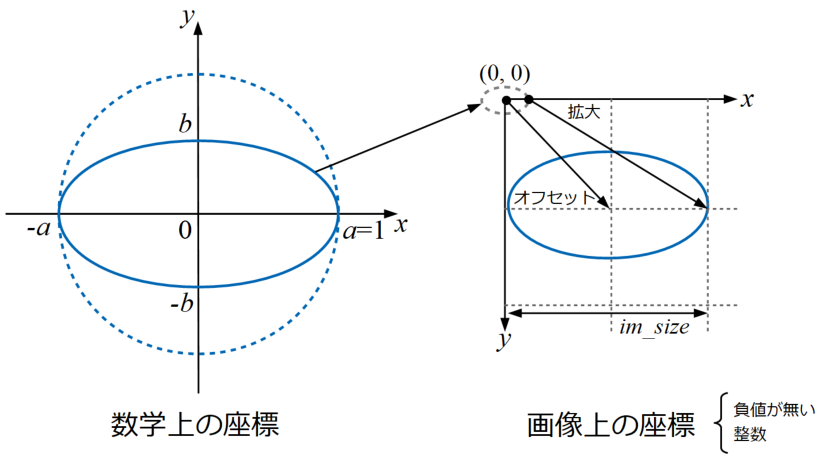
そのため以下の画像のように数学上の座標を画像上の座標に変換する作業が必要です。画像上の座標は負値が無いので、原点を中心とする楕円を画像内の中心にオフセットさせる必要があります。
そして楕円自体の大きさも半径1の単位円を基準に作った楕円では小さすぎます（1だと1ピクセルになります）。そのため拡大することが必要です。
さらに画像は全て整数で座標を指定する必要があるので、整数変換も必要です。
これらのオフセットと拡大、整数変換は「int((x[0, i] * im_size / 2) + im_size / 2)」でそれぞれの点毎に計算しています。
そしてforループで一つ一つ画像ファイルを保存していきますが、同じファイル名だとどんどん上書き保存されていってしまいますので、「path_out = path_head + '0' + str(i) + path_ext」でiというforループで増分されていく数値を使って文字列連結を行い、ファイル名が被らないようにしています。
後でフリーソフトでGIF動画を作る時に順番が入れ替わらないよう、画像のナンバリングには00, 01, ..., 10, 11...と一桁数には0を頭に付けるように条件分岐しています。
※0, 1, ...10, 11...という名前だと、フォルダ内で画像を名前順にした時に0, 10, 1, ...となってしまいます。
まとめ
このページでは楕円方程式で作成した点に画像の4点を対応させ、射影変換を用いてあたかも平面画像が立体的に回転しているような効果を出してみました。
プログラムは今回の注意点のみについて説明しましたが、ほとんどは「Pythonで平面を回転させる効果を表現する！」と「Python/OpenCVの射影変換なら簡単に画像補正ができる！」の記事内のコードと同じなので、是非そちらを参照してみて下さい。
大分画像処理らしいことができてきました！
Twitterでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています！
コメント