ディープラーニングにおける活性化関数をPythonで作る!

ニューラルネットワークに表現力を持たせるために必要な活性化関数には、様々な種類があります。ここでは代表的な活性化関数をいくつか紹介し、Pythonで関数化する所までを扱います。

こんにちは。wat(@watlablog)です。
Pythonの勉強とともに、AIや機械学習の勉強も始めました。このページでは、活性化関数について学んだことをまとめます！

目次（項目クリックでジャンプできます）

活性化関数でニューロンが多彩な表現力を持つ

ニューロンモデルは生物の仕組みを模倣している

人口知能の分野で知られるディープラーニングでは、多数のニューロンモデルと幾層ものネットワークで構成されたニューラルネットワークと呼ばれる構造を形成します。

以下の図は人間のニューロンをモデル化したものです。ニューロンは入力と重みとの積にバイアスを足し、活性化関数を経て出力信号を出すものと定義されています。

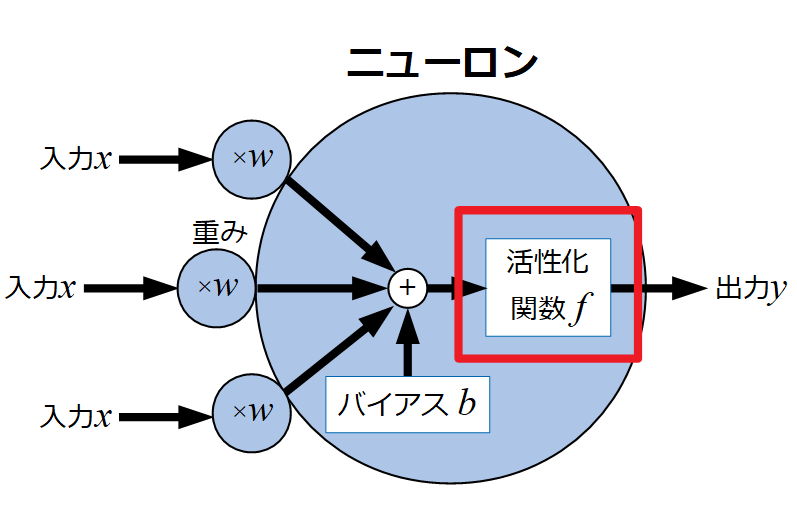
このページで扱うのは活性化関数ですが、上記説明だけでは数学的な言葉だけなので活性化関数について学ぶ前に、全体について少し生物学的なことも本を漁って調べてみました。

ニューロンにおける神経伝達物質とは？

1つのニューロンへ複数の入力がされているというのは、どうやら他の複数の神経細胞とによる神経伝達物質の授受を表現しているようです。この神経伝達物質にはグルタミン酸やガンマアミノ酪酸（GABA）等、現在では100種類以上も確認されているとのこと。

この神経伝達物質の受け取りはニューロンに複数あるレセプター分子で行うとのことですが、1つのレセプター分子は1つの神経伝達物質のみしか感じない（例えばGABAだけを感じるレセプター等）ことがわかっているそうです。

そして入力は複数ありますが、その物質から得られた信号は1つの軸索端末で処理されて次のニューロンに渡される…こうしてネットワークを形成していくということから、上図のニューロンモデルの出力は1つだけにしているそうです。

これらの生物学的な話は「Sebastian Seung(セバスチャン・スン), 青木薫（訳）, コネクト―ム脳の配線はどのように「わたし」をつくり出すのか, 草思社, (2015), pp.85-100」、

コネクトーム

セバスチャン・スン, 青木薫

2,640円(11/21 18:44時点)

楽天ブックス

モデルの話は「我妻幸長, はじめてのディープラーニング, SB Creative, (2018), pp.102-106」にわかりやすく書かれていますので、興味のある方には良書となると思います。

はじめてのディープラーニング

我妻幸長

2,948円(11/21 18:44時点)

楽天ブックス

入力$x$が神経伝達物質、受取部はレセプター分子で感度（重み$w$）があり、軸索端末を伝っていく過程に活性化関数$f$があって、出力部で再度神経伝達物質$y$が放出される…という理解で良いのかな？
バイアスはニューロン固有の興奮しやすさみたいなものかな？
この辺は是非専門家の意見をお聞きしたいですね。

活性化関数はニューロンの興奮を表現している

活性化関数はニューロンの興奮状態を表しています。

刺激（入力）に対して興奮するかしないか、といったことは脳にとっては極めて重要です。

全ての信号に対して毎回興奮する場合、または毎回興奮しない場合でもおそらく生物的に生きていくのは厳しいと思われます。

空腹時はラーメン見ると興奮するけど、満腹時はそうでもないもんね。
ラーメン見てトイレ行きたくなったりしても困るし、生物ってよくできてるね。

生物学的には神経伝達物質をニューロンで感じ（感じ方、感度は個々のレセプター分子やニューロン自体の感度による）、それを軸索端末で信号として伝えていき次のニューロンへ渡すということが行われているそうですが、

どうやらこれだけだとただ信号を伝えているだけで、ニューロンが多彩な表現力を持つことにはならないそうです。

先ほど紹介した書籍「コネクト―ム」の113ページには、「ある刺激でスパイクを起こさないニューロン（つまり行き止まり）も脳にとっては重要」と言及しています。

興奮の度合いは上図モデルの重み$w$やバイアス$b$で決まりますが、どういう形のスパイク（生物学的には活動電位）をどういうレベルでどんな時に起こすかもまた重要であることから、活性化関数というものが研究されているようです。

Pythonで活性化関数をコーディングしよう！

ステップ関数

\[ y=\begin{cases}
0 & (x\leq 0) \\
1 & (x > 0)
\end{cases}
\]

import numpy as np
#ステップ関数
def step(x):
    y = np.where(x <= 0, 0, 1)
    return y

import numpy as np

#ステップ関数

def step(x):

y = np.where(x <= 0, 0, 1)

return y

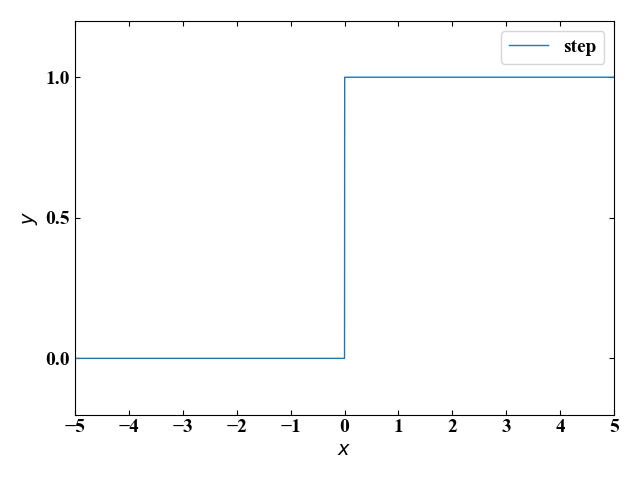
このステップ関数は入力$x$に対して0か1という2値をとります。場合分けにはNumPyのwhere関数を使っています。

1958年頃にパーセプトロンと呼ばれるニューラルネットワークの一種に使われていた、非常にシンプルな関数です。

パーセプトロン（wiki）

シグモイド関数

\[
y=\frac{1}{1+e^{-x}}
\]

import numpy as np
#シグモイド関数
def sigmoid(x):
    y = 1 / (1 + np.exp(-x))
    return y

import numpy as np

#シグモイド関数

def sigmoid(x):

y = 1 / (1 + np.exp(-x))

return y

シグモイド関数は入力$x$に対し0と1の間を滑らかに変化します。この関数は微分形が自身のシグモイド関数を用いて記述することができるため、古くからニューラルネットワークで利用されてきたそうです。

tanh（ハイパボリックタンジェント）

\[
y=\tanh=\frac{e^{x}-e^{-x}}{e^{x}+e^{-x}}
\]

import numpy as np
#ハイパボリックタンジェント関数
def tanh(x):
    y = np.tanh(x)
    return y

import numpy as np

#ハイパボリックタンジェント関数

def tanh(x):

y = np.tanh(x)

return y

シグモイド関数が0から1だったのに対して、tanhは-1から1までを滑らかに変化する関数で、負値を許容していることが特徴です。

ReLU

\[ y=\begin{cases}
0 & (x\leq 0) \\
x & (x > 0)
\end{cases}
\]

import numpy as np
#ReLU関数
def relu(x):
    y = np.where(x <= 0, 0, x)
    return y

import numpy as np

#ReLU関数

def relu(x):

y = np.where(x <= 0, 0, x)

return y

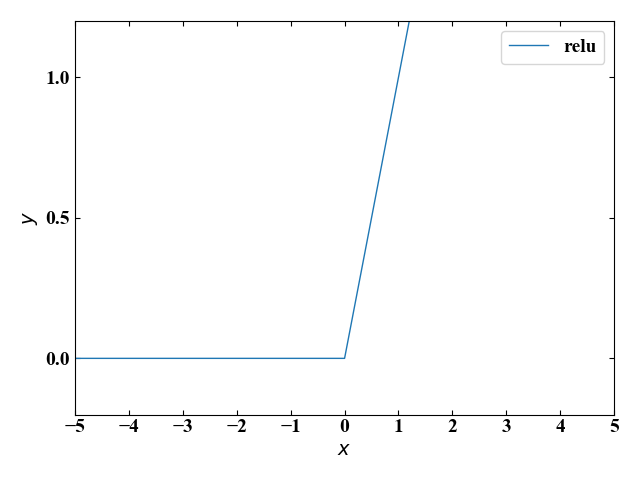
ReLU（Rectified Linear Unit）はランプ関数とも呼ばれます。シンプルなことと、多岐にわたる値を取れることからディープラーニングではよく使われる関数とのことです。
こちらも場合分けにはNumPyのwhere関数を使っています。

しかしこのReLUは条件によっては出力が0になり、学習が全く進まないdying ReLUという現象に陥る場合があるとのことです。

Leaky ReLU

\[ y=\begin{cases}
0.01x & (x\leq 0) \\
x & (x > 0)
\end{cases}
\]

import numpy as np
#Leaky ReLU関数
def lrelu(x):
    y = np.where(x <= 0, 0.01 * x, x)
    return y

import numpy as np

#Leaky ReLU関数

def lrelu(x):

y = np.where(x <= 0, 0.01 * x, x)

return y

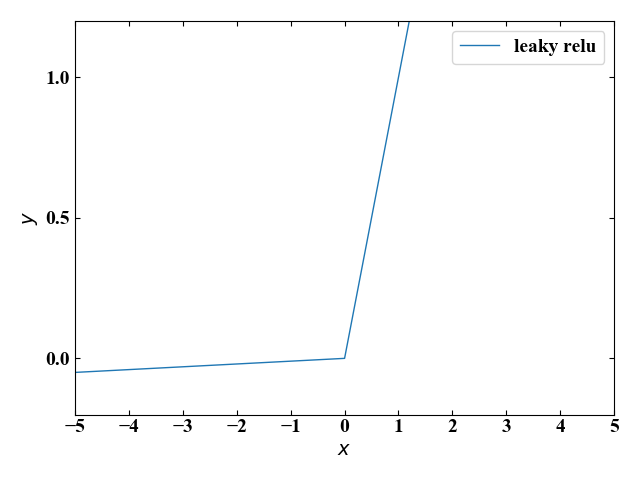
上記dying ReLU現象を改良するために生まれたのがこのLeaky ReLUです。入力$x$が負値の時に出力$y$が0にならないように小さな係数がかけてあります。

恒等関数

\[
y = x
\]

import numpy as np
#恒等関数
def identity(x):
    y = x
    return y

import numpy as np

#恒等関数

def identity(x):

y = x

return y

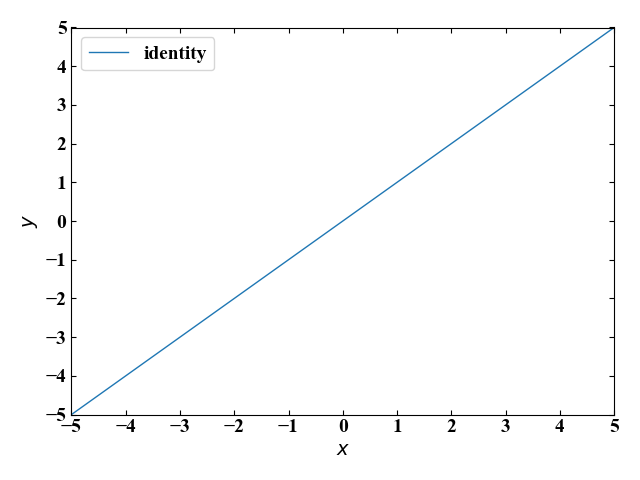
入力値をそのまま出力として返すのが恒等関数です。この関数はニューラルネットワークの出力層で主に回帰問題を扱う際によく使われるそうです。

ソフトマックス関数

\[
y=\frac{e^{x}}{\displaystyle \sum_{ k = 1 }^{ n } e^{x_{k}}}
\]

import numpy as np
#ソフトマックス関数
def softmax(x):
    y = np.exp(x) / np.sum(np.exp(x))
    return y

import numpy as np

#ソフトマックス関数

def softmax(x):

y = np.exp(x) / np.sum(np.exp(x))

return y

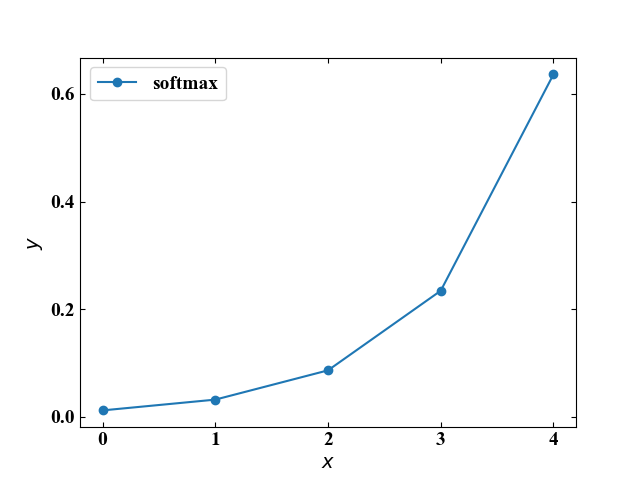
ソフトマックス関数は入力値の個数（$x_{k}$は同じ層のそれぞれの入力値を示す）によって値を変えますが、出力値の総和をとると1になることから、確率の要素を含む分類問題に対して使われるそうです。

まとめ

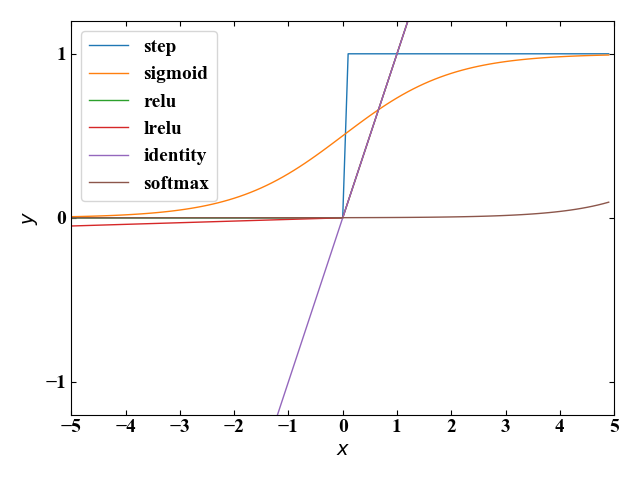
このページではディープラーニングで使用されるニューロンモデルと活性化関数の役割について学び、Pythonによる活性化関数のコーディングを行いました。

以下にまとめのコードを示します。

関数ファイル(activation_function.py)とメインファイル(main_activation.py)に分かれており、メインファイルを実行することで活性化関数がプロットされます。

関数ファイル

import numpy as np

#ステップ関数
def step(x):
    y = np.where(x <= 0, 0, 1)
    return y

#シグモイド関数
def sigmoid(x):
    y = 1 / (1 + np.exp(-x))
    return y

#ハイパボリックタンジェント関数
def tanh(x):
    y = np.tanh(x)
    return y

#ReLU関数
def relu(x):
    y = np.where(x <= 0, 0, x)
    return y

#Leaky ReLU関数
def lrelu(x):
    y = np.where(x <= 0, 0.01 * x, x)
    return y

#恒等関数
def identity(x):
    y = x
    return y

#ソフトマックス関数
def softmax(x):
    y = np.exp(x) / np.sum(np.exp(x))
    return y

import numpy as np

#ステップ関数

def step(x):

y = np.where(x <= 0, 0, 1)

return y

#シグモイド関数

def sigmoid(x):

y = 1 / (1 + np.exp(-x))

return y

#ハイパボリックタンジェント関数

def tanh(x):

y = np.tanh(x)

return y

#ReLU関数

def relu(x):

y = np.where(x <= 0, 0, x)

return y

#Leaky ReLU関数

def lrelu(x):

y = np.where(x <= 0, 0.01 * x, x)

return y

#恒等関数

def identity(x):

y = x

return y

#ソフトマックス関数

def softmax(x):

y = np.exp(x) / np.sum(np.exp(x))

return y

メインファイル

import activation_function as af
import numpy as np
from matplotlib import pyplot as plt

#x軸を生成
x = np.arange(-5, 5, 0.1)

#活性化関数を算出
y_step = af.step(x)
y_sigmoid = af.sigmoid(x)
y_tanh = af.tanh(x)
y_relu = af.relu(x)
y_lrelu = af.lrelu(x)
y_identity = af.identity(x)
y_softmax = af.softmax(x)

# ここからグラフ描画
# フォントの種類とサイズを設定する。
plt.rcParams['font.size'] = 14
plt.rcParams['font.family'] = 'Times New Roman'

# 目盛を内側にする。
plt.rcParams['xtick.direction'] = 'in'
plt.rcParams['ytick.direction'] = 'in'

# グラフの上下左右に目盛線を付ける。
fig = plt.figure()
ax1 = fig.add_subplot(111)
ax1.yaxis.set_ticks_position('both')
ax1.xaxis.set_ticks_position('both')

# 軸のラベルを設定する。
ax1.set_xlabel('$x$')
ax1.set_ylabel('$y$')

# データの範囲と刻み目盛を明示する。
ax1.set_xticks(np.arange(-10, 10, 1))
ax1.set_yticks(np.arange(-5, 5, 1))
ax1.set_xlim(-5, 5)
ax1.set_ylim(-1.2, 1.2)

# データプロットの準備とともに、ラベルと線の太さ、凡例の設置を行う。
ax1.plot(x, y_step, label='step', lw=1)
ax1.plot(x, y_sigmoid, label='sigmoid', lw=1)
ax1.plot(x, y_relu, label='relu', lw=1)
ax1.plot(x, y_lrelu, label='lrelu', lw=1)
ax1.plot(x, y_identity, label='identity', lw=1)
ax1.plot(x, y_softmax, label='softmax', lw=1)
fig.tight_layout()
plt.legend()

# グラフを表示する。
plt.show()
plt.close()

import activation_function as af

import numpy as np

from matplotlib import pyplot as plt

#x軸を生成

x = np.arange(-5, 5, 0.1)

#活性化関数を算出

y_step = af.step(x)

y_sigmoid = af.sigmoid(x)

y_tanh = af.tanh(x)

y_relu = af.relu(x)

y_lrelu = af.lrelu(x)

y_identity = af.identity(x)

y_softmax = af.softmax(x)

# ここからグラフ描画

# フォントの種類とサイズを設定する。

plt.rcParams['font.size'] = 14

plt.rcParams['font.family'] = 'Times New Roman'

# 目盛を内側にする。

plt.rcParams['xtick.direction'] = 'in'

plt.rcParams['ytick.direction'] = 'in'

# グラフの上下左右に目盛線を付ける。

fig = plt.figure()

ax1 = fig.add_subplot(111)

ax1.yaxis.set_ticks_position('both')

ax1.xaxis.set_ticks_position('both')

# 軸のラベルを設定する。

ax1.set_xlabel('$x$')

ax1.set_ylabel('$y$')

# データの範囲と刻み目盛を明示する。

ax1.set_xticks(np.arange(-10, 10, 1))

ax1.set_yticks(np.arange(-5, 5, 1))

ax1.set_xlim(-5, 5)

ax1.set_ylim(-1.2, 1.2)

# データプロットの準備とともに、ラベルと線の太さ、凡例の設置を行う。

ax1.plot(x, y_step, label='step', lw=1)

ax1.plot(x, y_sigmoid, label='sigmoid', lw=1)

ax1.plot(x, y_relu, label='relu', lw=1)

ax1.plot(x, y_lrelu, label='lrelu', lw=1)

ax1.plot(x, y_identity, label='identity', lw=1)

ax1.plot(x, y_softmax, label='softmax', lw=1)

fig.tight_layout()

plt.legend()

# グラフを表示する。

plt.show()

plt.close()

<広告>
人工知能のプロに最速でなるには、独学よりも効果的なオンラインゼミがあります。これを機会に是非ご検討下さい！

ついにディープラーニングの学習を始めました。様々な参考書やネットの情報を集めながら、それらを総合して理解を深めて行きたいと思います！

Twitterでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています！

参考文献

Sebastian Seung(セバスチャン・スン), 青木薫（訳）, コネクト―ム脳の配線はどのように「わたし」をつくり出すのか, 草思社, (2015）

我妻幸長, はじめてのディープラーニング, SB Creative, (2018)

活性化関数でニューロンが多彩な表現力を持つ

ニューロンモデルは生物の仕組みを模倣している

ニューロンにおける神経伝達物質とは？

活性化関数はニューロンの興奮を表現している

Pythonで活性化関数をコーディングしよう！

ステップ関数

シグモイド関数

tanh（ハイパボリックタンジェント）

ReLU

Leaky ReLU

恒等関数

ソフトマックス関数

まとめ

関数ファイル

メインファイル

参考文献

コメント

コメントを残すコメントをキャンセル

最近の投稿

アーカイブ

カテゴリー

活性化関数でニューロンが多彩な表現力を持つ

ニューロンモデルは生物の仕組みを模倣している

ニューロンにおける神経伝達物質とは？

活性化関数はニューロンの興奮を表現している

Pythonで活性化関数をコーディングしよう！

ステップ関数

シグモイド関数

tanh（ハイパボリックタンジェント）

ReLU

Leaky ReLU

恒等関数

ソフトマックス関数

まとめ

関数ファイル

メインファイル

参考文献

SNSでもご購読できます。

コメント

コメントを残す コメントをキャンセル

最近の投稿

アーカイブ

カテゴリー

コメントを残すコメントをキャンセル