
振動シミュレーションをプログラミングで行う場合、質量行列や剛性行列の記述が面倒です。しかし、ばね要素の結合と行列の重畳を理解する事で規則性を利用できます。ここではcsvに記録した質量や剛性の値を使ってPython/Numpy形式の行列生成を行う方法を紹介します。
こんにちは。wat(@watlablog)です。ここではPythonを使って振動モデルを自動生成する方法を紹介します!
なぜ振動モデルを自動生成したいのか?
本記事はほぼ筆者のメモですが、少しでも有益なページになると良いと思い、ここでコードのモチベーションを説明しておこうと思います。
スクリプトに直打ちするのはかなり面倒!
直列振動モデルの概要
このページで扱う直列振動モデルというのは、下図のようなばねマスが直列に繋がった系のことを指します。この図は2自由度モデルですが、これは振動を扱う人であれば見慣れた図だと思います。
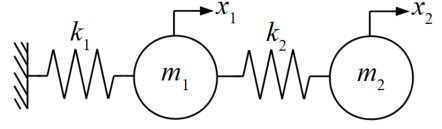
Pythonスクリプト表現の例
上のモデルをPythonスクリプトで表現すると下のコードのようになります。
|
1 2 3 4 5 |
# 質量マトリクスと剛性マトリクスを作成 M = np.array([[m1, 0], [0, m2]]) K = np.array([[k1 + k2, -k2], [-k2, k2]]) |
Numpyのndarrayで書いていますが、括弧を複数書いたりパラメータ同士を加算したり負値にしたりカンマで区切ったり…とスクリプト上で体裁を整えるのが面倒です(面倒でない?)。
自由度を変更した時に修正するのも面倒!
先ほどは2自由度モデルでしたが、3自由度になるとPythonでは以下のように書きます。
|
1 2 3 4 5 6 7 |
# 質量マトリクスと剛性マトリクスを作成 M = np.array([[m1, 0, 0], [0, m2, 0], [0, 0, m3]]) K = np.array([[k1 + k2, -k2, 0], [-k2, k2 + k3, -k3], [0, -k3, k3]]) |
自由度が1つ増えただけですが、行を追加するだけではなく各行全てを編集する必要があります。
自由度が増えたり減ったりするケースを検討する場合、いちいちスクリプト上でカンマを打ったり0を追加したりといった作業は意外と面倒です。
多自由度モデルを書くのも面倒!
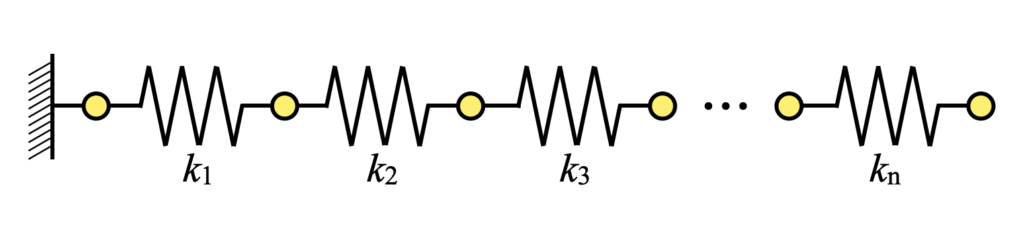
10自由度以下はまだなんとか頑張ろうという気にもなりますが、例えば100自由度のモデルを検討する必要が出てきた場合、これは最初の記述をするだけで面倒を通り越して無理だと思います(下図はn自由度直列振動モデル)。

絶対どこかで書き間違えをしてバグの原因にもなります。ここまでの自由度を検討する場合は自動化がマストだと思います。
また、このように多自由度の振動モデルを自動生成できるようになれば、振動シミュレーションに関しても最適化計算を適用したりしやすくなります。この記事はその方面に進むための足がかりとします。
自動生成の要件
それでは自動生成コードを書くために、どのようにやりたいことを実現するかの要件を書いておきます。
端部固定の直列振動系に限定する
今回は前提として直列のばねマス振動系を自動生成する方法を検討します。直列や並列、節点を飛び越したばねの接続は簡単化のため考えません。
複雑なモデルの場合はModelicaを使った1DCAEツールによる物理シミュレーションの方が良いと考えます。
下図のように一方の端部を固定したモデルを生成します。
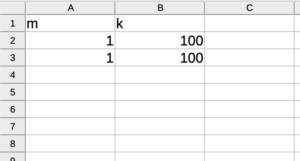
csvファイルからパラメータを読み取る
csvファイルにパラメータを任意の自由度分記録しておいて、それを読み取る形式とします。以下に2自由度の場合のcsvファイル例を示します。
列方向に質量、剛性列を作成し、行方向に自由度分数値を並べます。
ここで単位は質量が[kg], 剛性が[N/m]とします。単位系は任意に変えても構いませんが、後々シミュレーション結果で固有振動数が[Hz]になるようにと考えてこの単位系にしています。
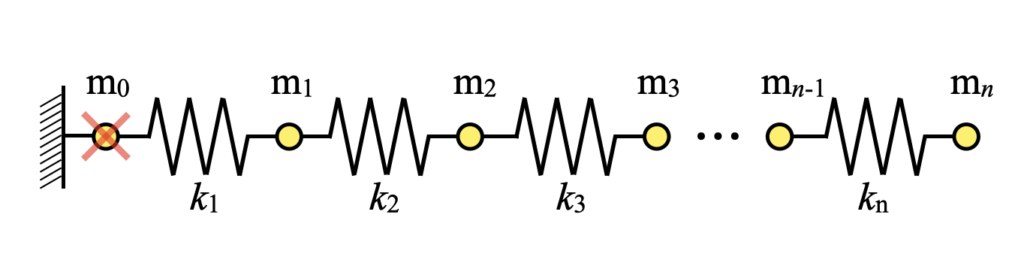
この時、端部固定を前提としているので、ファイルは以下の図に示すパラメータ位置関係となります(mとkの個数が同一になる)。
計算済の剛性行列を作る
最後は読み込んだ数値を基に、計算済の質量行列と剛性行列を作ります。
上記モデルの質量行列は対角行列となるので特に工夫は要りませんので、剛性行列の作り方に着目します。
剛性行列はばね要素の重畳と固定節点の性質から自動的に自由度分作成します。
ばね要素の結合と剛性行列の重畳について
プログラムで規則性を記述するために、ばねを直列に接続していった場合の剛性行列の変化を確認します。
まずは下図に示す単一のばね要素ですが、節点質量を0として節点周りの力関係から運動方程式を導くと式(1)となります。
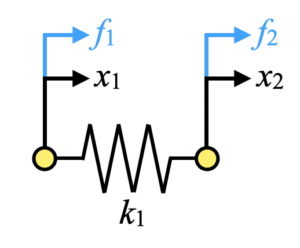
上式は行列形式で書くと式(2)となります。変位ベクトルの前にかかっている行列が剛性行列です。
運動方程式の立て方や行列形式の詳細は「Pythonで計算するために多自由度振動系を行列形式にする方法」にまとめていますのでこちらの記事を参照してください。
次に、下図のようにばね要素を1つ追加してみます。
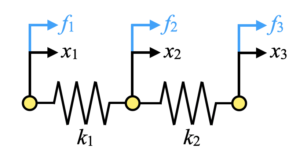
本モデルの運動方程式は式(3)です。外力ベクトルや変位ベクトルは単純に要素が増えただけですが、剛性行列は一部加算されている項目があります。
この加算のイメージを以下に図解します。単一のばね要素は同じ形の剛性行列を持ちますが、結合点の位置(ここでは\(x_{2}\)の節点と\(x_{3}\)の節点)で剛性行列を重畳させたことを意味しています。
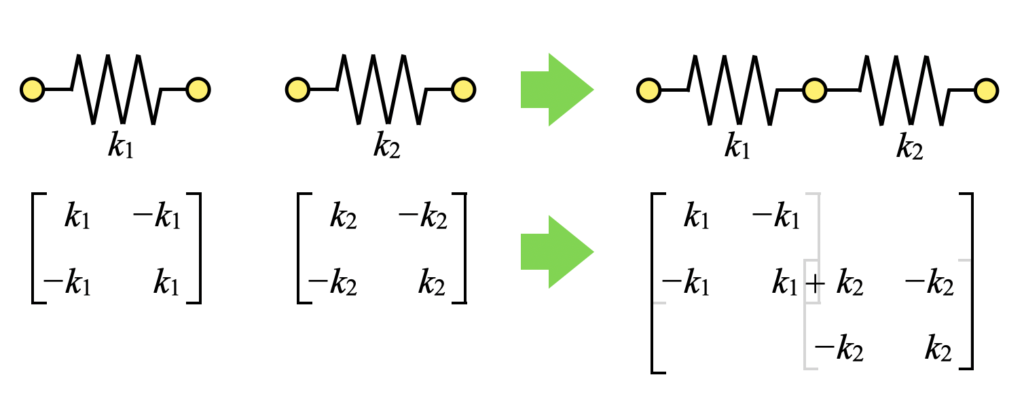
隣接節点を飛び越えた位置同士でばね要素を結合する場合は、結合させた節点位置に重畳させますが、直列モデルの場合はこの図を覚えておけば運動方程式を簡単に求めることが可能です。
固定した場合の剛性行列の変化について
先ほどまでのモデルは拘束をかけない(つまりフリーフリー)状態でしたが、今回は片方の端部を固定します。
拘束をかけると剛性行列は下図のように変化します。
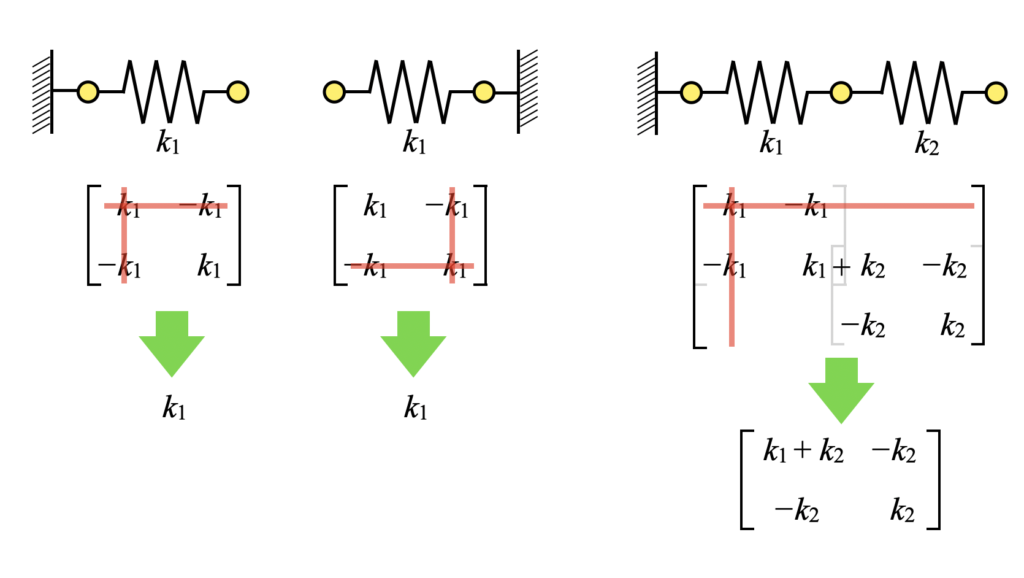
ばねが1つしかない場合はわかりやすく、どちらか一方を固定することで単一の剛性値となります。
これは固定することでその節点の動きがなくなるため、行列の該当要素を削除することを意味します。2自由度端部固定の場合の剛性行列は覚えている方も多いのではないでしょうか。
ここまででばね要素を結合していった場合と固定させた場合の剛性行列の変化を見てきました。
規則性がわかったので、n自由度の場合に拡張してコーディングしてみましょう。
csvファイルから質量・剛性行列を生成するコード
全コード
コードはとても簡単です。以下に全コードを示します。
まず、generate_matrix()関数の引数にファイル名を与え、pandasで読み込みます。
使ったファイルはこちら(ダウンロード可)。
読み込んだ値をそれぞれm, kとSeriesで抽出し、forループで剛性行列を作成します。forループではnp.zerosにより0で埋めた行列K_allに、単一のばね要素として作成したKを重畳させます。
重畳させる時にNumpyのスライスで位置をずらしながら、直列のばね要素の結合部で加算しています。
このK_allに対し、最後に固定を反映させるためnp.delete(操作する行列, 削除する指標, 方向(0:行, 1:列))を使います。
質量行列は1d配列を使って対角行列を作成すれば良いので、np.diag()で作成可能です。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 |
import numpy as np import pandas as pd # 質量行列と剛性行列をファイルから作成する関数 def generate_matrix(filename): # ファイルを読む df = pd.read_csv(filename, encoding='SHIFT-JIS') # 質量と剛性のリストを取り出す m = df['m'] k = df['k'] # フリーフリーの場合の剛性行列を生成する K_all = np.zeros([len(k) + 1, len(k) + 1]) for i in range(len(k)): # 単一ばね要素として剛性行列を定義する K = np.array([[k[i], -k[i]], [-k[i], k[i]]]) # iにより位置をシフトさせながらKを重畳する K_all[i:2 + i, i:2 + i] += K #print('i=',i, '\nK=\n', K_all) # デバッグ用 # 拘束を反映させる(第一節点の固定) K_all = np.delete(K_all, 0, axis=0) K_all = np.delete(K_all, 0, axis=1) # 質量行列を生成する M_all = np.diag(m) return M_all, K_all # 質量行列と剛性行列をファイルから作成する関数を実行 M, K = generate_matrix('2dof-system.csv') print('M=\n',M) print('K=\n',K) |
実行結果
こちらが実行結果です。2自由度は既に上の図解中の式で検算可能ですが、正しく作れているようです。
|
1 2 3 4 5 6 |
M= [[1 0] [0 1]] K= [[ 200. -100.] [-100. 100.]] |
100自由度でも確認してみる
次のファイルは100自由度の場合です。
以下が結果。どうやらうまくいっている様子。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
M= [[1 0 0 ... 0 0 0] [0 1 0 ... 0 0 0] [0 0 1 ... 0 0 0] ... [0 0 0 ... 1 0 0] [0 0 0 ... 0 1 0] [0 0 0 ... 0 0 1]] K= [[ 200. -100. 0. ... 0. 0. 0.] [-100. 200. -100. ... 0. 0. 0.] [ 0. -100. 200. ... 0. 0. 0.] ... [ 0. 0. 0. ... 200. -100. 0.] [ 0. 0. 0. ... -100. 200. -100.] [ 0. 0. 0. ... 0. -100. 100.]] |
振動シミュレーションで使えるか確認する
参考記事と使用するcsvファイル
本来目的である振動のシミュレーションで使う事ができるかどうか確認します。
今回は周波数応答解析や固有値解析による検証を行います。
周波数応答解析については「振動モデルを直接法の周波数応答解析で解くPythonコード」、固有値解析については「Pythonで多自由度系の固有値解析!固有振動数とモードを計算」の記事に詳細を紹介していますので、是非読んでみてください。
先ほどの100自由度のファイルだと固有値がかなり隣接していて効果が確認し難かったため、今回は以下の10自由度のファイルを使います。
全コード
以下が全コードです。詳細は先ほどの記事に記載した通りですが、今回は自動生成した質量と剛性行列がこれらのシミュレーションで使えるかどうかを確認します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 |
import numpy as np import pandas as pd from matplotlib import pyplot as plt # 質量行列と剛性行列をファイルから作成する関数 def generate_matrix(filename): # ファイルを読む df = pd.read_csv(filename, encoding='SHIFT-JIS') # 質量と剛性のリストを取り出す m = df['m'] k = df['k'] # フリーフリーの場合の剛性行列を生成する K_all = np.zeros([len(k) + 1, len(k) + 1]) for i in range(len(k)): # 単一ばね要素として剛性行列を定義する K = np.array([[k[i], -k[i]], [-k[i], k[i]]]) # iにより位置をシフトさせながらKを重畳する K_all[i:2 + i, i:2 + i] += K #print('i=',i, '\nK=\n', K_all) # デバッグ用 # 拘束を反映させる(第一節点の固定) K_all = np.delete(K_all, 0, axis=0) K_all = np.delete(K_all, 0, axis=1) # 質量行列を生成する M_all = np.diag(m) return M_all, K_all # Rayleigh dampingのパラメータを決定して減衰マトリクスを生成する関数 def generate_rayleigh_damping(f1, f2, zeta1, zeta2, M, K): # 指定周波数を角振動数に変換 w1 = 2 * np.pi * f1 w2 = 2 * np.pi * f2 # alphaとbetaを使って減衰行列を計算 alpha = (2 * w1 * w2 * (zeta2 * w1 - zeta1 * w2)) / (w1 ** 2 - w2 ** 2) beta = (2 * (zeta1 * w1 - zeta2 * w2)) / (w1 ** 2 - w2 ** 2) C = np.array(alpha * M + beta * K) return C # 周波数応答解析を計算する関数 def frequency_response_analysis(M, K, C, freq_l, freq_u, step, exc_node, res_node): steps = 2 * np.pi * np.arange(freq_l, freq_u, step) # 角振動数軸 excitation = np.ones_like(steps) # 加振力[N]の周波数波形 n_dofs = len(M) # 自由度の総数 F = np.zeros((len(steps), n_dofs)) # 周波数毎の外力ベクトルを初期化 # 角振動数分解能毎に計算するループ X = [] for i in range(len(steps)): F[i][exc_node] = excitation[i] # 外力ベクトルの更新 matrix = (-steps[i] ** 2) * M + (1j * steps[i] * C) + K # 逆行列にする前の行列を計算しておく inv_matrix = np.linalg.inv(matrix) # 逆行列計算 xn = np.dot(inv_matrix, F[i])[res_node] # 方程式を解き、複素変位ベクトルを求める xn = np.sqrt(xn.real ** 2 + xn.imag ** 2) # 振幅成分を計算する X.append(xn) return steps, X # 固有値解析を計算する関数 def eigen(M, K): # 質量マトリクスの逆行列を計算 M_inv = np.linalg.inv(M) # 固有値と固有ベクトルを計算 omega, v = np.linalg.eig(np.dot(M_inv, K)) # 固有値の順番を昇順にソート omega_sort = np.sqrt(np.sort(omega)) # (1 / (2 * np.pi)) * # 固有値のソート時のインデックスを取得 sort_index = np.argsort(omega) # 固有値に対応する固有ベクトルをソート v_sort = [] for i in range(len(sort_index)): v_sort.append(v.T[sort_index[i]]) v_sort = np.array(v_sort) return omega_sort, v_sort, sort_index # 質量行列と剛性行列をファイルから作成する関数を実行 M, K = generate_matrix('10dof-system.csv') print('M=\n',M) print('K=\n',K) # 減衰マトリクスを計算する関数を実行 C = generate_rayleigh_damping(f1=1, f2=100, zeta1=0.2, zeta2=0.1, M=M, K=K) # 周波数応答解析を実行 freq_axis, X = frequency_response_analysis(M=M, K=K, C=C, freq_l=1, freq_u=100, step=0.05, exc_node=1, res_node=1) freq_axis = freq_axis * (1 / (2 * np.pi)) # 固有値解析を実行(確認用) omega, v, index = eigen(M, K) print('Natural frequency[Hz]=', omega * (1 / (2 * np.pi))) # ここからグラフ描画 # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure() ax1 = fig.add_subplot(111) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') # スケール設定 ax1.set_xscale('log') ax1.set_yscale('log') # 軸のラベルを設定する。 ax1.set_xlabel('Excitation frequency [Hz]') ax1.set_ylabel('Displacement[m]') ax1.plot(freq_axis, X, lw=1, color='red', label='Analysis Result') # レイアウトと凡例の設定 fig.tight_layout() plt.legend() # グラフを表示する。 plt.show() plt.close() |
固有値解析結果
コンソールに出力される固有振動数の結果はこちらです。1.0[Hz]以上50[Hz]未満の範囲で分布しているようです。
|
1 2 |
Natural frequency[Hz]= [ 2.37873276 7.08306132 11.62916599 15.91549431 19.84629679 23.33376579 26.29999702 28.67872978 30.41682711 31.47546278] |
周波数応答解析結果
周波数応答解析の結果はmatplotlibによるプロットで表示されます。先ほどの固有振動数の位置でピークが立っていることが確認できました。
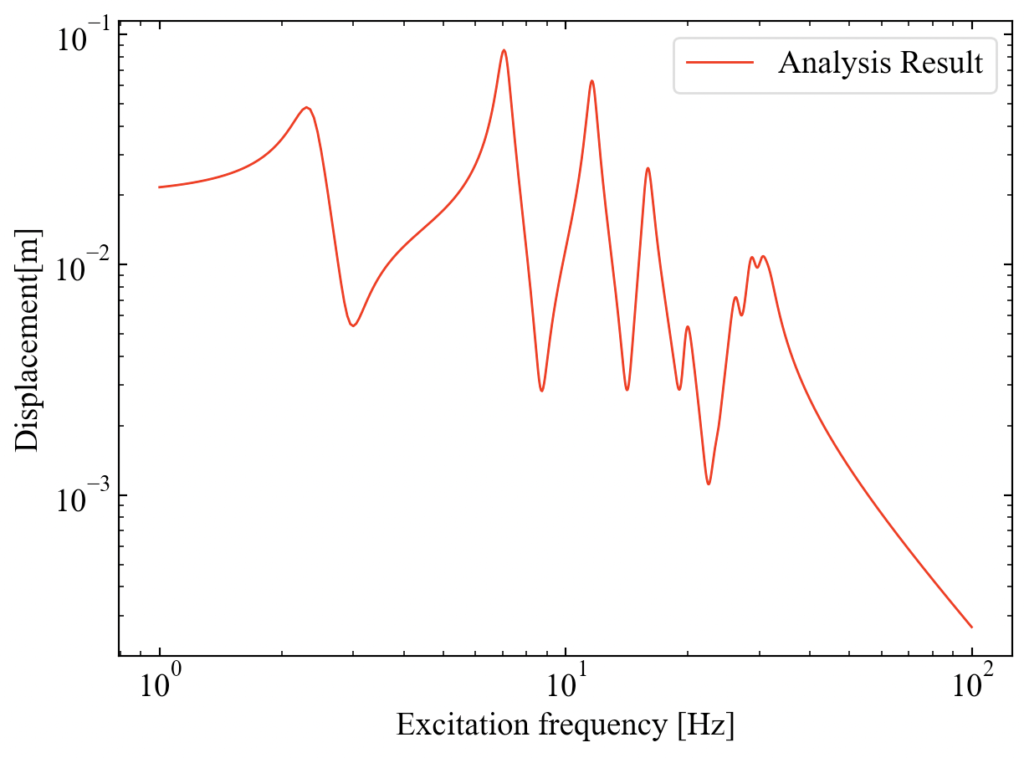
以上から、今回自動生成した質量行列と剛性行列はPythonによる振動シミュレーションで十分使用できることが確認されました。
まとめ
今回はこれまでPythonコード内に直接記述していた多自由度振動系のパラメータをcsvから読み込んで行列生成してみました。
これでn自由度のパラメータをいちいちコード上に記載しなくてもよくなりそうです。
Numpyを使えば高速に行列生成ができるようです!
Twitterでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています!

 ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!
ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!