モータやエンジンといった回転機は構造の共振に当たらないように加振力を設計する必要があります。ここではPythonで回転数変化を模擬した周波数応答解析を行い、実験の次数トラッキング解析と比較できるシミュレーション結果を得る事を目標とします。
こんにちは。wat(@watlablog)です。ここでは覚えたての周波数応答解析で回転数変化を模擬した加振力の計算してみます!
※本記事は過去に学んだ内容の応用、小Tipsです!
本記事の対象者
加振力の変化を考慮した周波数応答解析をしたい人
前回の記事「振動モデルを直接法の周波数応答解析で解くPythonコード」ではPythonを使って振動モデルの周波数応答解析を行い、各周波数における振動応答のレベルを計算できるようになりました。
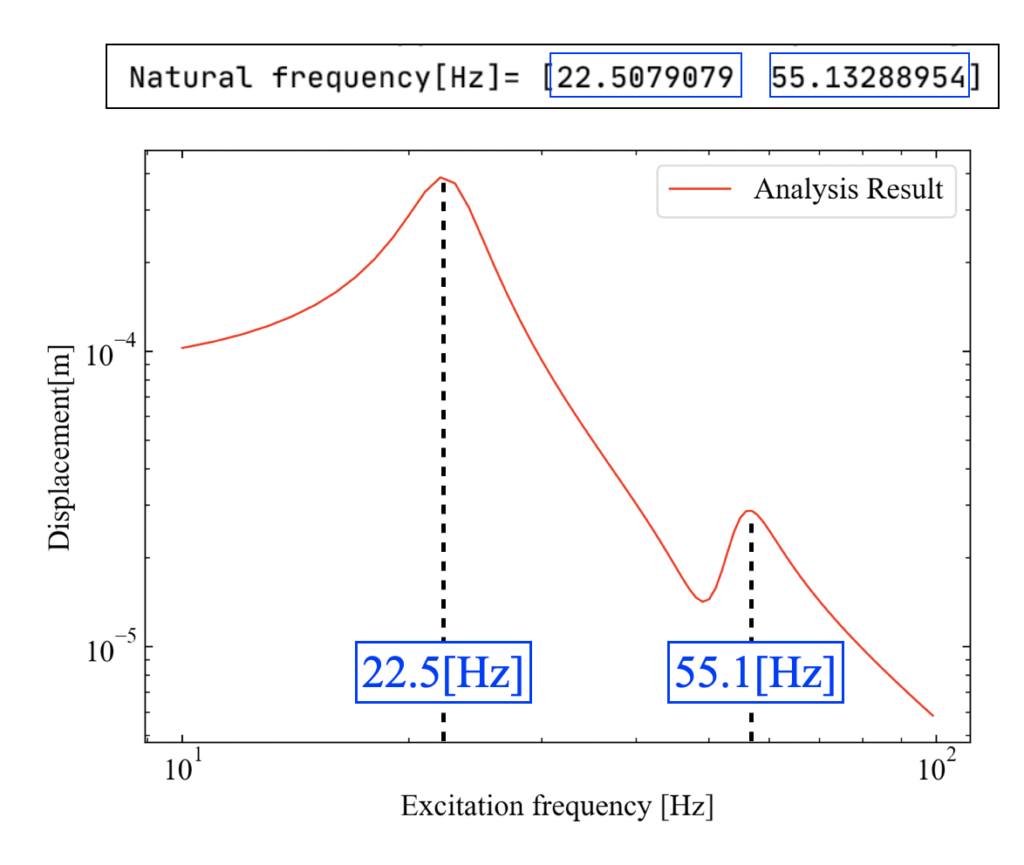
下図はホワイトノイズ加振時の2自由度振動モデルにおける振動応答を計算した結果例です。共振のピークが2つ確認できます。
一般的には、周波数応答解析では下図の関係を計算する手法です。
伝達関数\(H\)は物理的に振動モデルを構築した時点で持つ特性の事で、評価点において単位荷重当たりにどれくらいの振動が発生するかを意味しています。
伝達関数\(H\)と入力(加振力)\(F\)を掛け合わせた結果、最終的な振動応答\(X\)が計算されます。
下図は実際に前回記事のコードで計算した結果ですが、入力のピークが伝達関数のラインに乗って振幅が決まっている様子がよくわかると思います。
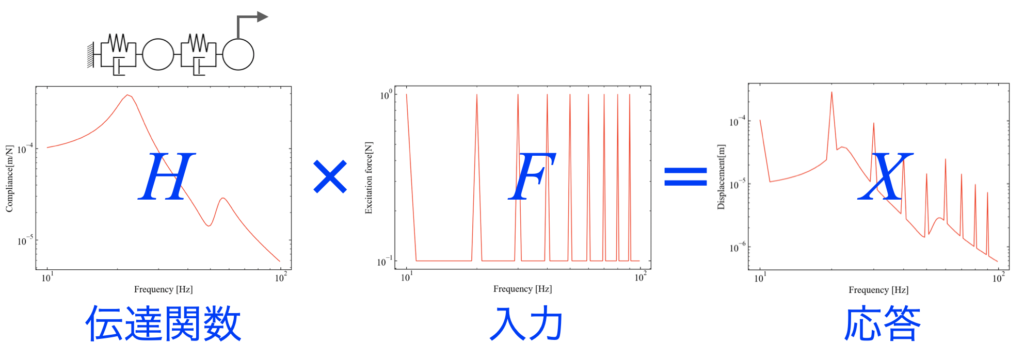
今回の記事は周波数応答解析の高速性を利用し、加振力が変化した時の振動応答を計算したい人を対象にしています。
イメージとしては、下図のようにモータ駆動時の加速度振動や変位振動をセンサーで計測している状況を考えます。
モータの回転数は一定ではなく、使用状況によって様々に変化します。回転機の振動を計測すると、1回転に1回振動が発生する基本次数(回転1次)の他に、基本次数の等倍で発生する高調波次数(回転N次)も発生します。
横軸に回転数[rpm]、縦軸に周波数[Hz]、色レベルを応答振動で表現すると、回転機の振動は下図のスペクトログラムのようなプロットになります。
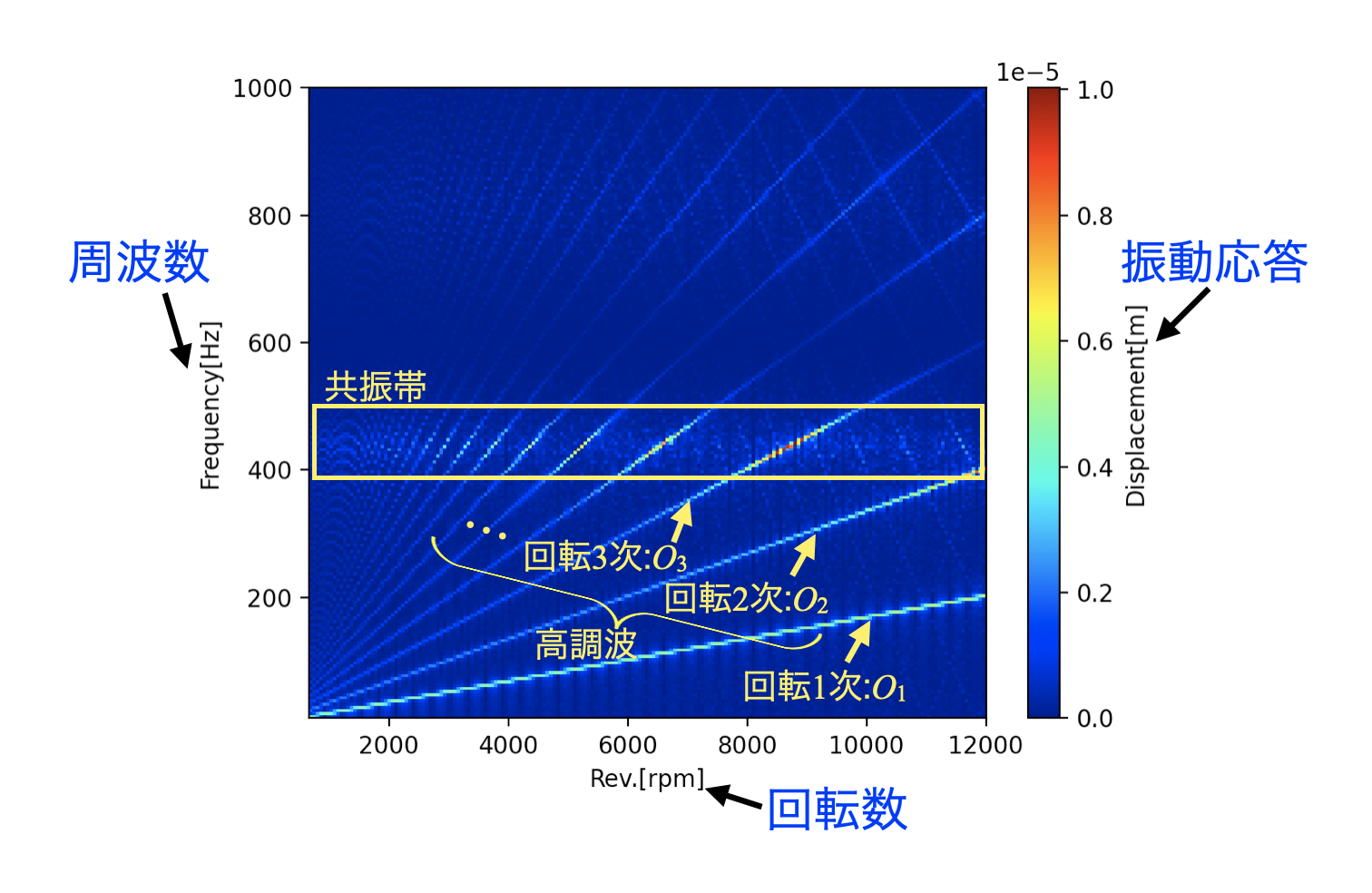
次数の線は回転数が増加すると周波数も増加するため、斜めに線が引かれる形になりますが、構造物の共振(固有振動数)は回転数に拠らず一定です。
周波数変化する回転次数が周波数で一定の共振帯と一致すると急激に応答振動のレベルが増大するため、故障や音振動のクレーム原因になり得ます。
共振はスペクトログラムの横一線でぼやっと明るくなるので、見た目で判断する事もできます。いちいち実験モーダル解析や固有値解析をしなくても、ざっくり知る事ができて便利ですね。
共振は構造物に必ず存在しますが、できるだけ製品の使用範囲外になるように設計したり、どうしても避けられない場合は材料や構造、制御方式を工夫したりといった事を検討します。
周波数応答解析はこのような設計検討で大変重宝される解析手法です。今回はPythonを使って上記モータのような加振力が変化する場合の周波数応答解析をコーディングしてみます。
加振力の変化を考慮した周波数応答解析のPythonコード
動作環境
このページに記載のコードは以下のPC環境で検証しました。参考までに。
PC
| Windows | OS | Windows10 64bit |
|---|---|---|
| CPU | 2.4[GHz] | |
| メモリ | 4[GB] |
| Mac | OS | macOS Catalina 10.15.7 |
|---|---|---|
| CPU | 1.4[GHz] | |
| メモリ | 8[GB] |
Python環境
Python環境は以下です。外部ライブラリはNumpyと結果可視化用にmatplotlibを使っています。
| Python | Python 3.7.7 |
|---|---|
| PyCharm (IDE) | PyCharm CE 2020.1 |
| Numpy | 1.19.0 |
| matplotlib | 3.2.2 |
モデル定義
今回も理解する事を優先させて、2自由度振動系を定義します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
# シミュレーションモデル def model(): # 質量・剛性の集中定数を設定する m1 = 0.05 m2 = 0.01 k1 = 500000 k2 = 200000 # 質量マトリクスと剛性マトリクスを作成 M = np.array([[m1, 0], [0, m2]]) K = np.array([[k1 + k2, -k2], [-k2, k2]]) return M, K |
変化する加振力を作成
変化する加振力セットは以下の関数で作成します。dataとして時間波形を作成した後にフーリエ変換して周波数波形にするという作り方をしています。周波数応答解析時にそのまま使えるように周波数分解能やサンプリングレートをサンプリングの定理に則って設定しています。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
# 擬似加振力スイープ周波数波形の作成 def freq_wave(freq_l, freq_u, step, f_base, f_max): samplerate = freq_u * 2.56 # サンプリングレート[Hz]は上限周波数の2.56倍 dt = 1 / samplerate # 時間刻み[s] end = 1 / step # 周波数分解能を周波数応答解析のステップにあわせる[s] t = np.arange(0, end + dt, dt) # 時間軸[s] n = int((freq_u - freq_l) / step) # 計算ステップ数 f_increment = (f_max - f_base) / n # ステップ当たりの回転数[rps]変化 amp_list = [] rpms = [] for i in range(n): freq_i = f_base + (i + 1) * f_increment rpms.append(freq_i * 60) # 基本周波数をRPMに変換 #data = signal.sawtooth(2 * np.pi * freq_i * t) # のこぎり波 data = np.sin(2 * np.pi * freq_i * t) # 正弦波 amp, freq = calc_fft(data, samplerate) # フーリエ変換 amp_sub = amp[int(freq_l / step):int(freq_u)] # 周波数応答解析で使用する範囲のみ振幅を抽出 amp_list.append(amp_sub) freq_sub = freq[int(freq_l / step):int((freq_u + step) / step)] # 周波数応答解析で使用する範囲のみ周波数軸を抽出 return amp_list, freq_sub, rpms |
補足:実用的な加振力データを作るには
今回はサンプルとしてPython上で理想的な波形を生成していますが、実際の設計では製品にどのような外力が加わるのかをよく分析して設定する事が重要です。
例えばモータであれば、モータ内部のステータやロータに働く電磁力を別途磁界解析を行なって得るといった事が実用的には考えられます。
他にも機構部品がぶつかったり摩擦によって力が発生したり…解析の目的に応じて外力の詳細度や種類を検討する必要があります。
周波数応答解析の関数を修正
「振動モデルを直接法の周波数応答解析で解くPythonコード」は関数の内部で加振波形を作っていましたが、今回は関数の引数excitationとして波形を渡す形で書いてみました。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
# 周波数応答解析を計算する関数 def frequency_response_analysis(M, K, C, steps, exc_node, res_node, excitation): steps = steps * 2 * np.pi # 周波数を角振動数に変換 n_dofs = len(M) # 自由度の総数 F = np.zeros((len(steps), n_dofs)) # 周波数毎の外力ベクトルを初期化 # 角振動数分解能毎に計算するループ X = [] for i in range(len(steps)-1): F[i][exc_node] = excitation[i] # 外力ベクトルの更新 matrix = (-steps[i] ** 2) * M + (1j * steps[i] * C) + K # 逆行列にする前の行列を計算しておく inv_matrix = np.linalg.inv(matrix) # 逆行列計算 xn = np.dot(inv_matrix, F[i])[res_node] # 方程式を解き、複素変位ベクトルを求める xn = np.sqrt(xn.real ** 2 + xn.imag ** 2) # 振幅成分を計算する X.append(xn) steps = steps / (2 * np.pi) return steps, X |
メイン関数の部分で先ほど作成した加振力セットを1行ずつ抽出し、周波数応答解析を実行する事で加振力が変化する分析を行います。
|
1 2 3 4 5 6 7 8 9 10 11 |
# 周波数応答解析を実行 X_list = [] for i in range(len(amp)): freq_axis, X = frequency_response_analysis(M=M, K=K, C=C, steps=freq, exc_node=1, res_node=1, excitation=amp[i]) X_list.append(X) |
全コード(コピペ用)
以下にコピペ用全コードを示します。減衰の考え方等は一緒ですが、フーリエ変換関数を追加したり、前回記事とはちょこちょこ変更していますので、コード内コメントもご確認下さい。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 |
import numpy as np from scipy import signal from scipy import fftpack from matplotlib import pyplot as plt # シミュレーションモデル def model(): # 質量・剛性の集中定数を設定する m1 = 0.05 m2 = 0.01 k1 = 500000 k2 = 200000 # 質量マトリクスと剛性マトリクスを作成 M = np.array([[m1, 0], [0, m2]]) K = np.array([[k1 + k2, -k2], [-k2, k2]]) return M, K # Rayleigh dampingのパラメータを決定して減衰マトリクスを生成する関数 def generate_rayleigh_damping(f1, f2, zeta1, zeta2, M, K): # 指定周波数を角振動数に変換 w1 = 2 * np.pi * f1 w2 = 2 * np.pi * f2 # alphaとbetaを使って減衰行列を計算 alpha = (2 * w1 * w2 * (zeta2 * w1 - zeta1 * w2)) / (w1 ** 2 - w2 ** 2) beta = (2 * (zeta1 * w1 - zeta2 * w2)) / (w1 ** 2 - w2 ** 2) C = np.array(alpha * M + beta * K) return C # 周波数応答解析を計算する関数 def frequency_response_analysis(M, K, C, steps, exc_node, res_node, excitation): steps = steps * 2 * np.pi # 周波数を角振動数に変換 n_dofs = len(M) # 自由度の総数 F = np.zeros((len(steps), n_dofs)) # 周波数毎の外力ベクトルを初期化 # 角振動数分解能毎に計算するループ X = [] for i in range(len(steps)-1): F[i][exc_node] = excitation[i] # 外力ベクトルの更新 matrix = (-steps[i] ** 2) * M + (1j * steps[i] * C) + K # 逆行列にする前の行列を計算しておく inv_matrix = np.linalg.inv(matrix) # 逆行列計算 xn = np.dot(inv_matrix, F[i])[res_node] # 方程式を解き、複素変位ベクトルを求める xn = np.sqrt(xn.real ** 2 + xn.imag ** 2) # 振幅成分を計算する X.append(xn) steps = steps / (2 * np.pi) return steps, X # 固有値解析を計算する関数 def eigen(M, K): # 質量マトリクスの逆行列を計算 M_inv = np.linalg.inv(M) # 固有値と固有ベクトルを計算 omega, v = np.linalg.eig(np.dot(M_inv, K)) # 固有値の順番を昇順にソート omega_sort = (1 / (2 * np.pi)) * np.sqrt(np.sort(omega)) # 固有値のソート時のインデックスを取得 sort_index = np.argsort(omega) # 固有値に対応する固有ベクトルをソート v_sort = [] for i in range(len(sort_index)): v_sort.append(v.T[sort_index[i]]) v_sort = np.array(v_sort) return omega_sort, v_sort, sort_index # フーリエ変換をする関数 def calc_fft(data, samplerate): spectrum = fftpack.fft(data) # 信号のフーリエ変換 amp = np.sqrt((spectrum.real ** 2) + (spectrum.imag ** 2)) # 振幅成分 amp = amp / (len(data) / 2) # 振幅成分の正規化(辻褄合わせ) phase = np.arctan2(spectrum.imag, spectrum.real) # 位相を計算 phase = np.degrees(phase) # 位相をラジアンから度に変換 freq = np.linspace(0, samplerate, len(data)) # 周波数軸を作成 return amp, freq # 擬似加振力スイープ周波数波形の作成 def freq_wave(freq_l, freq_u, step, f_base, f_max): samplerate = freq_u * 2.56 # サンプリングレート[Hz]は上限周波数の2.56倍 dt = 1 / samplerate # 時間刻み[s] end = 1 / step # 周波数分解能を周波数応答解析のステップにあわせる[s] t = np.arange(0, end + dt, dt) # 時間軸[s] n = int((freq_u - freq_l) / step) # 計算ステップ数 f_increment = (f_max - f_base) / n # ステップ当たりの回転数[rps]変化 amp_list = [] rpms = [] for i in range(n): freq_i = f_base + (i + 1) * f_increment rpms.append(freq_i * 60) # 基本周波数をRPMに変換 #data = signal.sawtooth(2 * np.pi * freq_i * t) # のこぎり波 data = np.sin(2 * np.pi * freq_i * t) # 正弦波 amp, freq = calc_fft(data, samplerate) # フーリエ変換 amp_sub = amp[int(freq_l / step):int(freq_u)] # 周波数応答解析で使用する範囲のみ振幅を抽出 amp_list.append(amp_sub) freq_sub = freq[int(freq_l / step):int((freq_u + step) / step)] # 周波数応答解析で使用する範囲のみ周波数軸を抽出 return amp_list, freq_sub, rpms # モデルの質量マトリクスと剛性マトリクスを求める関数を実行 M, K = model() # 減衰マトリクスを計算する関数を実行 C = generate_rayleigh_damping(f1=10, f2=1000, zeta1=0.2, zeta2=0.1, M=M, K=K) # サンプルの加振力周波数波形を作成 freq_l = 10 freq_u = 1000 step = 5 f_base = 10 f_max = 500 amp, freq, rpms = freq_wave(freq_l=freq_l, freq_u=freq_u, step=step, f_base=f_base, f_max=f_max) # 周波数応答解析を実行 X_list = [] for i in range(len(amp)): freq_axis, X = frequency_response_analysis(M=M, K=K, C=C, steps=freq, exc_node=1, res_node=1, excitation=amp[i]) X_list.append(X) # 固有値解析を実行(確認用) omega_sort, v_sort, index= eigen(M, K) print('Natural frequency[Hz]=', omega_sort) # ここからグラフ描画 # グラフをオブジェクト指向で作成する。 fig = plt.figure() ax1 = fig.add_subplot(111) # データをプロットする。 im = ax1.pcolormesh(rpms, freq_axis, np.array(X_list).T, cmap='jet', vmin=0, vmax=np.max(X_list)) # カラーバーを設定する。 cbar = fig.colorbar(im) cbar.set_label('Displacement[m]') # 軸設定する。 ax1.set_xlabel('Rev.[rpm]') ax1.set_ylabel('Frequency[Hz]') # グラフを表示する。 plt.show() plt.close() |
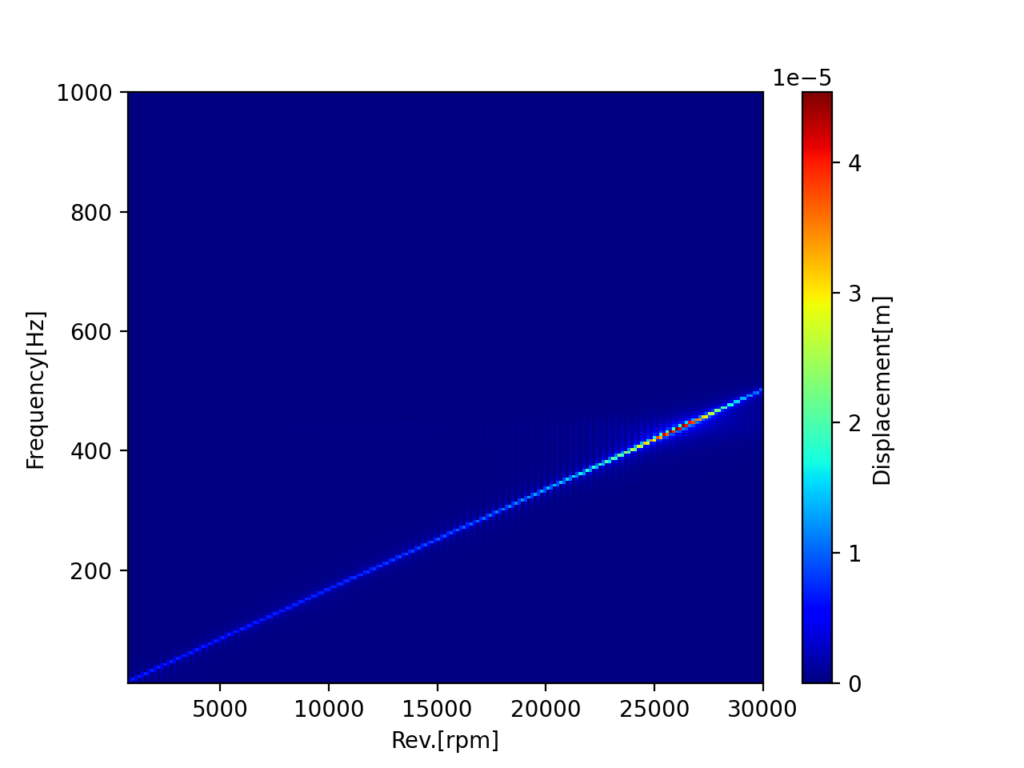
単一次数の結果
上記コードの実行結果は下図です。共振である400[Hz]付近に次数が当たった部分で振幅大となっています。
高調波次数も追加してみる
続いて、先ほどの加振力セットの関数内のdata部分コメント蘭を切り替えて、のこぎり波バージョンにしてみます。のこぎり波は基本周波数の高調波が出るので、今回のように高調波を出したい時によく使います。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
# 擬似加振力スイープ周波数波形の作成 def freq_wave(freq_l, freq_u, step, f_base, f_max): samplerate = freq_u * 2.56 # サンプリングレート[Hz]は上限周波数の2.56倍 dt = 1 / samplerate # 時間刻み[s] end = 1 / step # 周波数分解能を周波数応答解析のステップにあわせる[s] t = np.arange(0, end + dt, dt) # 時間軸[s] n = int((freq_u - freq_l) / step) # 計算ステップ数 f_increment = (f_max - f_base) / n # ステップ当たりの回転数[rps]変化 amp_list = [] rpms = [] for i in range(n): freq_i = f_base + (i + 1) * f_increment rpms.append(freq_i * 60) # 基本周波数をRPMに変換 data = signal.sawtooth(2 * np.pi * freq_i * t) # のこぎり波 #data = np.sin(2 * np.pi * freq_i * t) # 正弦波 amp, freq = calc_fft(data, samplerate) # フーリエ変換 amp_sub = amp[int(freq_l / step):int(freq_u)] # 周波数応答解析で使用する範囲のみ振幅を抽出 amp_list.append(amp_sub) freq_sub = freq[int(freq_l / step):int((freq_u + step) / step)] # 周波数応答解析で使用する範囲のみ周波数軸を抽出 return amp_list, freq_sub, rpms |
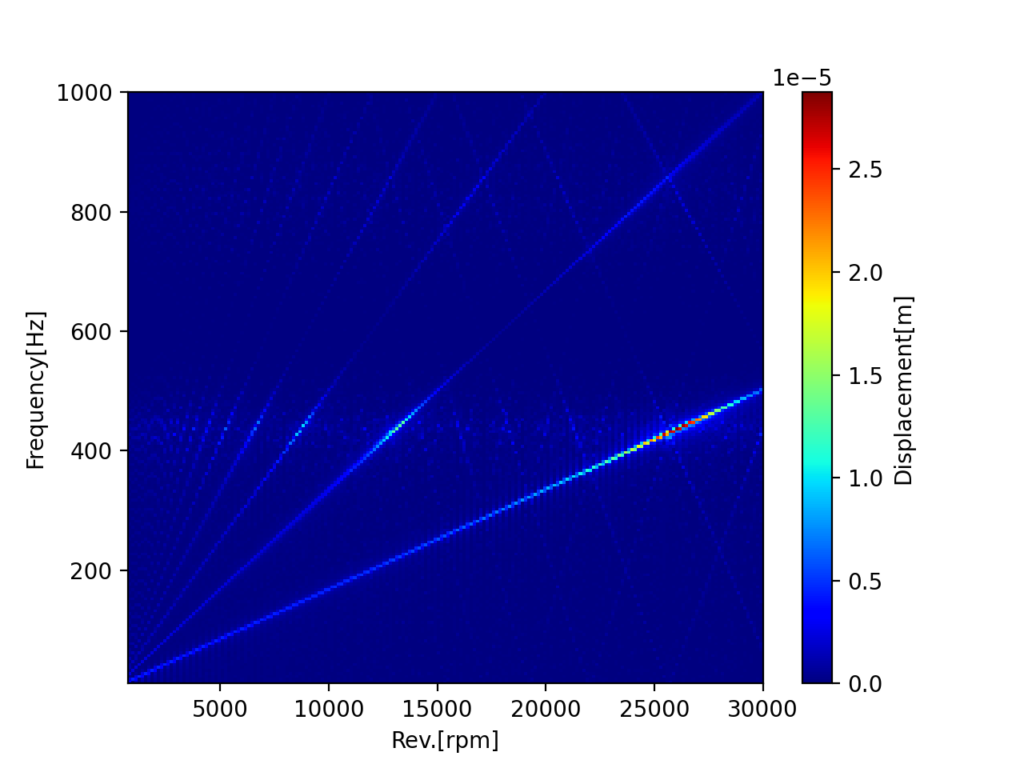
結果は以下です。複数次数が発生していますが、共振に当たる400[Hz]付近で振幅レベルが増大している結果を得る事ができました。
ちなみに800[Hz]ちょいにも共振があり、薄ら明るくなっている事に気づきましたでしょうか(2自由度なので)?
全コード内には固有値解析コードも付いていますので、是非パラメータを色々変えて遊んでみて下さい。
まとめ
本記事では「振動モデルを直接法の周波数応答解析で解くPythonコード」で学んだ周波数応答解析の応用として、小修正で加振力を変化させてみました。
特に新しい式やアルゴリズムは登場していませんが、学んだ技術でこんな事ができるのは非常に面白いと思いました。
ちょっと考えた事がすぐ実現できるのはPythonのメリットだと思いますので、是非皆さんも始めてみて下さい!
周波数応答解析は便利なので、加振力を色々変えてみてシミュレーションしてみるのも面白いですね!
Twitterでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています!

 ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!
ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!